–ú–Ķ—Ä–ĺ–ľ–ĺ—Ä—Ą–Ĺ–į —Ą—É–Ĺ–ļ—Ü—Ė—Ź
|
Read other articles:

Shabana AzmiAzmi di Apsara Film Awards pada 2015 Anggota Parlemen (Nominasi)Masa jabatan27 Agustus 1997 ‚Äď 26 Agustus 2003 Informasi pribadiLahirShabana Kaifi Azmi18 September 1950 (umur 73)Hyderabad, Negara Bagian Hyderabad, India(sekarang Telangana, India)Suami/istriJaved Akhtar (m. 1984)Orang tuaKaifi AzmiShaukat KaifiPekerjaanPemeran, Penggiat sosialSunting kotak info ‚ÄĘ L ‚ÄĘ B Shabana Azmi (lahir 18 September 1950) adalah seorang ...

Bendera Armenia Nama ‘Ķ’ľ’°’£’ł÷ā’Ķ’∂ (YeŇôaguyn) Pemakaian Bendera nasional Perbandingan 1:2 Dipakai 24 Agustus 1990 Rancangan Triwarna mendatar berwarna merah, biru, dan jingga Perancang Stepan Malkhasyants Varian bendera Bendera Armenia Pemakaian Standar presidensial Perbandingan 1:2 Bendera nasional Armenia, Triwarna Armenia (bahasa Armenia: ‘Ķ’ľ’°’£’ł÷ā’Ķ’∂, YeŇôaguyn), terdiri dari tiga bidang horizontal dengan lebar yang sama, merah di bagian atas, biru di tengah, dan jingga (juga...

Cernaycomune Cernay ‚Äď Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Alto Reno ArrondissementThann CantoneCernay TerritorioCoordinate47¬į49‚Ä≤N 7¬į10‚Ä≤E / 47.816667¬įN 7.166667¬įE47.816667; 7.166667ÔĽŅ (Cernay)Coordinate: 47¬į49‚Ä≤N 7¬į10‚Ä≤E / 47.816667¬įN 7.166667¬įE47.816667; 7.166667ÔĽŅ (Cernay) Superficie18,03 km¬≤ Abitanti11 539[1] (2009) Densit√†639,99 ab./km¬≤ Altre informazioniCod. postale68700 Fuso orario...

Serena Williams Serena Williams nel 2021 Nazionalit√† Stati Uniti Altezza 180 cm Peso 72 kg Tennis Termine carriera 3 settembre 2022 Carriera Singolare1 Vittorie/sconfitte 858 ‚Äď 156 (84.62%) Titoli vinti 73 Miglior ranking 1¬™ (8 luglio 2002) Risultati nei tornei del Grande Slam Australian Open V (2003, 2005, 2007, 2009, 2010, 2015, 2017) Roland Garros V (2002, 2013, 2015) Wimbledon V (2002, 2003, 2009, 2010, 2012, 2015, 2016) US Open V (1999, 2002, 2008, 2012...

„Āď„ĀģŤ®ėšļč„ĀĮś§úŤ®ľŚŹĮŤÉĹ„Ā™ŚŹāŤÄÉśĖáÁĆģ„āĄŚáļŚÖł„ĀĆŚÖ®„ĀŹÁ§ļ„Āē„āĆ„Ā¶„ĀĄ„Ā™„ĀĄ„Āč„ÄĀšłćŚćĀŚąÜ„Āß„Āô„ÄāŚáļŚÖł„āíŤŅŌ䆄Āó„Ā¶Ť®ėšļč„ĀģšŅ°ť†ľśÄߌźĎšłä„Āę„ĀĒŚćĒŚäõ„ĀŹ„Ā†„Āē„ĀĄ„ÄāÔľą„Āď„Āģ„ÉÜ„É≥„Éó„ɨ„Éľ„Éą„ĀģšĹŅ„ĀĄśĖĻԾȌáļŚÖłś§úÁīĘ?: „ā≥„Éę„āĮ ‚Äď „Éč„É•„Éľ„āĻ ¬∑ śõłÁĪć ¬∑ „āĻ„āę„É©„Éľ ¬∑ CiNii ¬∑ J-STAGE ¬∑ NDL ¬∑ dlib.jp ¬∑ „āł„É£„ÉĎ„É≥„āĶ„Éľ„ÉĀ ¬∑ TWLÔľą2017ŚĻī4śúąÔľČ „ā≥„Éę„āĮ„āíśČď„Ā°śäú„ĀĄ„Ā¶šĹú„Ā£„ĀüÁď∂„Āģś†ď „ā≥„Éę„āĮÔľąśú®ś†ď„ÄĀÔŅĹ...
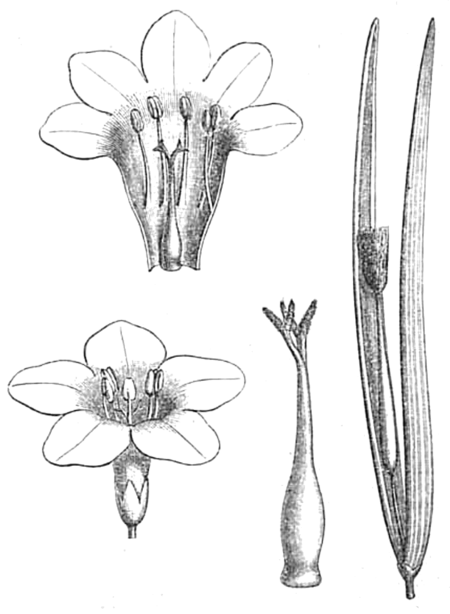
Plocospermataceae Plocosperma buxifolium Klasifikasi ilmiah Kerajaan: Plantae (tanpa takson): Tracheophyta (tanpa takson): Angiospermae (tanpa takson): Eudikotil (tanpa takson): Asterid (tanpa takson): Lamiid Ordo: Lamiales Famili: Plocospermataceae Genera lihat teks. Plocospermataceae adalah salah satu famili anggota tumbuhan berbunga. Menurut Sistem klasifikasi APG II suku ini termasuk dalam ordo Lamiales. Wikimedia Commons memiliki media mengenai Plocospermataceae. Pengidentifikasi takson...

Australian politician (1950‚Äď2022) The HonourablePeter ReithAMReith in 2001Minister for DefenceIn office30 January 2001 ‚Äď 26 November 2001Prime MinisterJohn HowardPreceded byJohn MooreSucceeded byRobert HillMinister for Employment and Workplace RelationsIn office21 October 1998 ‚Äď 30 January 2001Prime MinisterJohn HowardPreceded byDavid KempSucceeded byTony AbbottMinister for Small BusinessIn office18 July 1997 ‚Äď 30 January 2001Prime MinisterJohn HowardPrecede...

French court official Kneeling, in a stained-glass window Room of Madeleine of Savoy, as set up in the National Museum of the Renaissance at the Ch√Ęteau d'√Čcouen, which she built with her husband. Madeleine of Savoy (1510‚Äď1586) was a French court official, Premi√®re dame d'honneur to the queen of France, Elisabeth of Austria, from 1570 until 1574. Life Madeleine was the daughter of Ren√© of Savoy and Anne Lascaris.[1] She married constable Anne de Montmorency, a leading soldier an...

Church in AustraliaSt Patrick's Church, Mount PerrySt Patricks Church, 200925¬į10‚Ä≤47‚Ä≥S 151¬į38‚Ä≤32‚Ä≥E / 25.1798¬įS 151.6421¬įE / -25.1798; 151.6421Address18 Pearson Street, Mount Perry, North Burnett Region, QueenslandCountryAustraliaDenominationRoman CatholicWebsitewww.childerscatholic.netHistoryStatusChurchConsecrated12 February 1905 (1905-02-12)ArchitectureArchitect(s)F H FairclothArchitectural typeChurchStyleGothic RevivalCompleted1904Specific...

ś≠§śĚ°ÁõģŚļŹŤ®ÄÁꆍäāś≤°śúČŚÖÖŚąÜśÄĽÁĽďŚÖ®śĖáŚÜÖŚģĻŤ¶ĀÁāĻ„Äā (2019ŚĻī3śúą21śó•)ŤĮ∑ŤÄÉŤôϜȩŚÖÖŚļŹŤ®ÄԾƜłÖśôįś¶āŤŅįśĚ°ÁõģśČÄśúČťá杼ě„ÄāŤĮ∑Śú®śĚ°ÁõģÁöĄŤģ®Ťģļť°ĶŤģ®Ťģļś≠§ťóģťĘė„Äā ŚďąŤź®ŚÖčśĖĮŚĚ¶ÁłĹÁĶĪŚďąŤĖ©ŚÖčÁłĹÁĶĪśóóÁŹĺšĽĽ“ö–į—Ā—č–ľ-–Ė–ĺ–ľ–į—Ä—ā –ö–Ķ–ľ–Ķ–Ľ“Ī–Ľ—č –Ę–ĺ“õ–į–Ķ–≤Ść°ÁĎüŚßÜŤč•ť©¨ŚįĒÁČĻ¬∑śČėŚć°ŤÄ∂Ś§ęŤá™2019ŚĻī3śúą20śó•Śú®šĽĽšĽĽśúü7ŚĻīť¶ĖšĽĽŚä™ŚįĒŤčŹšłĻ¬∑Áļ≥śČéŚįĒŚ∑īŤÄ∂Ś§ęŤģĺÁęč1990ŚĻī4śúą24śó•ÔľąŚďąŤĖ©ŚÖčŤėáÁ∂≠ŚüÉÁ§ĺśúÉšłĽÁĺ©ŚÖĪŚíĆŚúčÁłĹÁĶĪÔľČ ŚďąŤź®ŚÖčśĖĮŚĚ¶ ŚďąŤź®ŚÖčśĖĮŚĚ¶śĒŅŚļú...

Red supergiant star in the constellation Carina CK Carinae An I band (near infrared) light curve for CK Carinae, plotted from ASAS data[1] Observation dataEpoch J2000 Equinox J2000 Constellation Carina Right ascension 10h 24m 25.36s[2] Declination ‚ąí60° 11′ 29.0″[2] Apparent magnitude (V) 7.2 - 8.5[3] Characteristics Spectral type M3.5 Iab[4] B‚ąíV color index +2.21[2]...

Bilateral relationsChilean‚ÄďAmerican relations Chile United States Diplomatic missionEmbassy of Chile, Washington, D.C.Embassy of the United States, SantiagoEnvoyChilean Ambassador to the United States Juan Gabriel Vald√©sAmerican Ambassador to Chile Bernadette M. Meehan Chilean President Gabriel Boric with U.S. President Joe Biden at the Summit of the Americas in Los Angeles; June 2022. The relationship between Chile and the United States, which dates back to the 19th century, has improved ...

20th-century tradition of Western philosophy Part of a series onPhilosophy Philosophy portal Contents Outline Lists Glossary History Categories Disambiguation Philosophies By period Ancient Ancient Egyptian Ancient Greek Medieval Renaissance Modern Contemporary Analytic Continental By region African Egypt Ethiopia South Africa Eastern philosophy Chinese Indian Indonesia Japan Korea Vietnam Indigenous American Aztec philosophy Middle Eastern philosophy Iranian Western American British Fren...

P. V. Narasimha Rao Telangana Veterinary UniversityFormer namesHyderabad Veterinary College, Sri P. V. Narasimha Rao Telangana State University for Veterinary, Animal and Fishery SciencesTypePublicEstablished2014ChancellorGovernor of TelanganaVice-ChancellorSri.Adhar Sinha, IAS[1]LocationHyderabad, Telangana, India17¬į19‚Ä≤34‚Ä≥N 78¬į24‚Ä≤30‚Ä≥E / 17.326235¬įN 78.4083168¬įE / 17.326235; 78.4083168AffiliationsICARWebsitetsvu.nic.in P. V. Narasimha Rao Telangana...

Alain BashungAlain Bashung en 2007.BiographieNaissance 1er décembre 194714e arrondissement de Paris (France)Décès 14 mars 2009 (à 61 ans)14e arrondissement de Paris (France)Sépulture Cimetière du Père-LachaiseNom dans la langue maternelle Alain BaschungNom de naissance Alain Claude BaschungPseudonymes Alain Bashung, Hendrick Darmen, David BergenNationalité françaiseActivités Acteur, auteur-compositeur-interprètePériode d'activité 1966-2009Conjoints Chantal Mironneau (d) (de ...

Eccellenza SardegnaSport Calcio Tiposquadre di club FederazioneFIGC - Comitato Sardegna Parte diEccellenza Paese Italia Cadenzaannuale Aperturasettembre Chiusuramaggio Partecipanti17 Formula1 Girone all'italiana con play-off e play-out Promozione inSerie D Retrocessione inPromozione (calcio) Sito Internethttps://www.figc-sardegna.it/ StoriaFondazione1991 Numero edizioni33 Detentore Ilvamaddalena Record vittorie Ilvamaddalena (3) Ultima edizioneEccellenza Sardegna 2022-2023 Ediz...
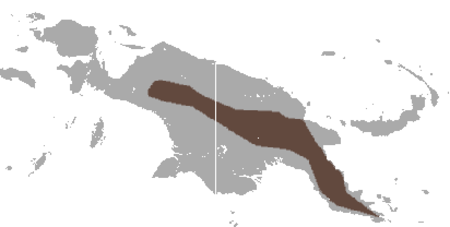
Species of marsupial Silky cuscus[1] Conservation status Least Concern (IUCN 3.1)[2] Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Infraclass: Marsupialia Order: Diprotodontia Family: Phalangeridae Genus: Phalanger Species: P. sericeus Binomial name Phalanger sericeusThomas, 1907 Silky cuscus range The silky cuscus (Phalanger sericeus) is a species of marsupial in the family Phalangeridae. It is found in Indonesia and...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Michael Paget ‚Äď berita ¬∑ surat kabar ¬∑ buku ¬∑ cendekiawan ¬∑ JSTOR Michael PagetInformasi latar belakangNama lahirMichael PagetLahir12 September 1978 (umur 45)Bridgend, South WalesGenreHeavy metal, m...

4¬į33‚Ä≤25‚Ä≥N 95¬į42‚Ä≤23‚Ä≥E / 4.557078¬įN 95.706259¬įE / 4.557078; 95.706259 Arongan LambalekKecamatanNegara IndonesiaProvinsiAcehKabupatenAceh BaratPemerintahan ‚ÄĘ CamatMawardi,SPD[1]Populasi (2015)[2] ‚ÄĘ Total11,928 jiwa ‚ÄĘ Kepadatan166/km2 (430/sq mi)Kode pos23652Kode Kemendagri11.05.07 Kode BPS1107062 Luas130,06 km¬≤[3]Desa/kelurahan27Situs webaronganlambalek.acehbaratkab.go.id Arongan Lamba...

Polish politician JarosŇāaw ZieliŇĄskiMember of the SejmIncumbentAssumed office 25 September 2005Constituency24 ‚Äď BiaŇāystok Personal detailsBorn1960NationalityPolishPolitical partyLaw and Justice JarosŇāaw ZieliŇĄski (born 20 September 1960 in Szwajcaria) is a Polish politician. He was elected to the Sejm on 25 September 2005, getting 15780 votes in 24 BiaŇāystok district as a candidate from the Law and Justice list. He was also a member of Sejm 2001-2005. See also Members of Polish Se...





























