Коваріантна похідна
|
Read other articles:

Panicum repens Klasifikasi ilmiah Kerajaan: Plantae Divisi: Tracheophyta Kelas: Liliopsida Ordo: Poales Famili: Poaceae Genus: Panicum Spesies: P. repens Nama binomial Panicum repensL. Panicum repens adalah spesies tumbuhan yang tergolong ke dalam famili Poaceae. Spesies ini juga merupakan bagian dari ordo Poales. Spesies Panicum repens sendiri merupakan bagian dari genus Panicum.[1] Nama ilmiah dari spesies ini pertama kali diterbitkan oleh L.. Referensi ^ Panicum. The Plant Li...

Ahsan Iqbal Menteri Dalam Negeri ke-35Masa jabatan4 Agustus 2017 – 31 Mei 2018PresidenMamnoon HussainPerdana MenteriShahid Khaqan AbbasiWakilMuhammad Talal Chaudhry PendahuluNisar Ali KhanPenggantiMuhammad Azam Khan (pelaksana tugas)Menteri Perencanaan, Pembangunan dan ReformasiMasa jabatan16 September 2017 – 31 Mei 2018PresidenMamnoon HussainPerdana MenteriShahid Khaqan Abbasi PendahuluDiri sendiriPenggantiShamshad AkhtarMasa jabatan7 Juni 2013 – 28 Juli 2017...

ObsidianObsidian yang ditemukan di Oregon'sUmumKategoriBatuan vulkanikIdentifikasiWarnaHitam pekat atau hitam kehijauanFrakturKonkoidalKekerasan dalam skala Mohs5–6[1]KilauKekacaanBerat jenissekitar 2,4[2]Sifat optikTranslusenSifat lainTekstur: halus seperti kacaReferensi[3] Obsidian, batu kendan[4] , atau batu kaca[5] adalah kaca vulkanik alami yang berupa batuan beku ekstrusif.[6][7] Obsidian terbentuk dari ekstrusi lava felsik yang ...

Untuk perusahaan Bugatti yang sekarang, lihat Bugatti Automobiles SAS. BugattiIndustriOtomotifNasibDijual ke Hispano-Suiza tahun 1963Didirikan1909PendiriEttore BugattiKantorpusatMolsheim, PrancisTokohkunciEttore Bugatti (penemu) Jean BugattiProdukMobil, bagian pesawat Mobil Ettore Bugatti adalah mobil Prancis produsen dari mobil kinerja tinggi, yang didirikan pada tahun 1909 . Mobil Bugatti yang dikenal karena keindahan desain mereka (Ettore Bugatti adalah dari keluarga seniman dan menganggap...

Mountain pass in Lower Austria This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Klostertaler Gscheid – news · newspapers · books · scholar · JSTOR (March 2024) (Learn how and when to remove this template message) Klostertaler GscheidKlostertaler Gscheid with ChapelElevation764 m (2,507 ft)Traversed byRoadLoca...

1952 film O. Henry's Full HouseTheatrical film posterDirected byHenry KosterHenry HathawayJean NegulescoHoward HawksHenry KingScreenplay byRichard L. BreenWalter BullockPhilip DunneIvan GoffBen HechtNunnally JohnsonCharles LedererBen RobertsLamar TrottiBased onShort storiesby O. HenryProduced byAndré HakimStarringFred Allen Anne BaxterJeanne CrainFarley GrangerCharles LaughtonOscar Levant Marilyn MonroeJean PetersGregory RatoffDale RobertsonDavid WayneRichard WidmarkNarrated byJohn Steinbeck...

Piala Super Saudi Berain 2020TurnamenPiala Super Saudi Al-Hilal Al-Nassr Liga Pro Piala Raja 0 3 Tanggal30 Januari 2021 (2021-01-30)StadionStadion Internasional Raja Fahd, RiyadhWasitDaniele Orsato (Italia)[1]Penonton0[note 1]CuacaBerawan15 °C (59 °F)Kelembapan35%← 2019 2021 → Piala Super Saudi 2020 (juga dikenal sebagai Piala Super Saudi Berain untuk alasan sponsor) adalah edisi ke-7 Piala Super Saudi, pertandingan sepak bola tahunan yang dimainka...

Maddalena GonzagaBartolomeo Melioli, medaglia di Maddalena Gonzaga.Signora consorte di Pesaro In carica1489 – 1490 PredecessoreCamilla Marzano d'Aragona SuccessoreLucrezia Borgia NascitaMantova, 10 luglio 1472 MortePesaro, 8 agosto 1490 DinastiaGonzaga PadreFederico I Gonzaga MadreMargherita di Baviera Consorte diGiovanni Sforza ReligioneCattolicesimo Maddalena Gonzaga (Mantova, 10 luglio 1472 – Pesaro, 8 agosto 1490) era figlia di Federico I Gonzaga, marchese di Mantova, e di Margh...

1090–1273 Nizari state in northwest Iran and Syria It has been suggested that this article be merged into Order of Assassins. (Discuss) Proposed since September 2023. Nizari Ismaili state1090–1273 Left: Flag until 1162, Right: Flag after 1162CapitalAlamut Castle (Assassins of Persia, main headquarters)Masyaf Castle (Assassins of the Levant)Common languagesPersian (in Iran)[1]Arabic (in the Levant)[1]Religion Nizari Ismaili Shia IslamGovernmentTheocratic absolute monar...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: コルク – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL(2017年4月) コルクを打ち抜いて作った瓶の栓 コルク(木栓、�...

Ta-a miMi Ta-aSajianHidangan utamaTempat asalTaiwanDaerahNasionalDibuat olehOrang TaiwanSuhu penyajianHangatBahan utamaMie gandum Tiongkok, sup rasa udang, udang, ketumbar, Saus Daging Taiwan, dan bawang putihSunting kotak info • L • BBantuan penggunaan templat ini Media: Ta-a mi Ta-a mi [1] ( Hanzi: 擔仔麵; Pinyin: dànzǎimiàn; Pe̍h-ōe-jī: tàⁿ-á-mī; harfiah: 'shoulder pole noodle' ), juga dikenal sebagai mie Ta-a atau mie danzai, a...

Questa voce sull'argomento videogiochi di ruolo è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Final Fantasy Legend IIIvideogiocoLogo di Final Fantasy Legend IIITitolo originale時空の覇者 Sa・Ga3 [完結編] PiattaformaGame Boy, Nintendo DS Data di pubblicazioneGame Boy: 13 dicembre 1991 29 settembre 1993 Nintendo DS: 6 gennaio 2011[1] GenereVideogioco di ruolo alla giapponese TemaFa...
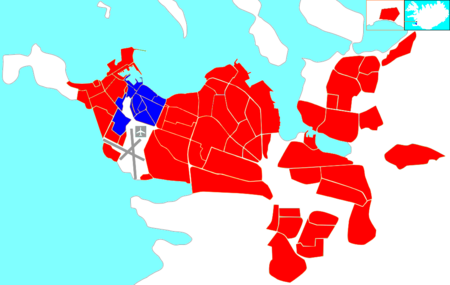
District in Reykjavík, IcelandCity Center MiðborgDistrictCountryIcelandMunicipalityReykjavíkArea • Total3.6 km2 (1.4 sq mi)Population (2010) • Total8,600 • Density2,400/km2 (6,200/sq mi)Postal codeIS-101 Reykjavík City Center (Icelandic: Miðborg [ˈmɪðˌpɔrk], Miðbær [ˈmɪðˌpaiːr̥], and sometimes Austurbær [ˈœystʏrˌpaiːr̥]) is a sub-municipal administrational district that covers much of...

Military leader and Emperor of the French Republic (1769–1821) For other uses, see Napoleon (disambiguation) and Napoleon Bonaparte (disambiguation). NapoleonThe Emperor Napoleon in His Study at the Tuileries, 1812Emperor of the French1st reign18 May 1804 – 6 April 1814SuccessorLouis XVIII[a]2nd reign20 March 1815 – 22 June 1815SuccessorLouis XVIII[a] First Consul of the French RepublicIn office13 December 1799 – 18 May 1804 Born(1769-08-15)15 August 1769Ajacc...

Grafik perjalanan kereta api Gapeka pada layar monitor Grafik perjalanan kereta api (gapeka) digunakan untuk mewakili pergerakan kereta api beserta waktu terhadap posisi masing-masing alat transportasi. Operasi pada jalur kereta api secara grafis ditampilkan dan direncanakan menggunakan gapeka. Dokumen terkait seperti teleks kereta luar biasa (KLB), warta maklumat (wam), dan maklumat kereta api (malka) umumnya diturunkan dari gapeka. Aplikasi gapeka tertua yang diketahui telah dibuat pada tah...

1926 film by Rowland V. Lee The Silver TreasureAdvertisementDirected byRowland V. LeeMike MigginsWritten byRobert N. Lee (scenario)Elizabeth Pickett Chevalier (titles)Based onNostromoby Joseph ConradProduced byWilliam FoxCinematographyG. O. PostDistributed byFox Film CorporationRelease dates June 19, 1926 (1926-06-19) (St. Petersburg, Florida) July 25, 1926 (1926-07-25) (New York City) Running time6 reelsCountryUnited StatesLanguageSilent (English interti...

Pour les articles homonymes, voir Leskovac (homonymie). Leskovac Лесковац Héraldique Drapeau Administration Pays Serbie Province Serbie centrale Région Jablanica District Jablanica Ville Leskovac Maire Goran Cvetanović (SRS) Code postal 16 00016 10416 10516 10616 107 Démographie Population 60 288 hab. (2011) Géographie Coordonnées 42° 59′ 53″ nord, 21° 56′ 46″ est Altitude 228 m Localisation Géoloc...

Religion by country Africa Algeria Angola Benin Botswana Burkina Faso Burundi Cameroon Cape Verde Central African Republic Chad Comoros Democratic Republic of the Congo Republic of the Congo Djibouti Egypt Equatorial Guinea Eritrea Eswatini Ethiopia Gabon Gambia Ghana Guinea Guinea-Bissau Ivory Coast Kenya Lesotho Liberia Libya Madagascar Malawi Mali Mauritania Mauritius Morocco Mozambique Namibia Niger Nigeria Rwanda São Tomé and Príncipe Senegal Seychelles Sierra Leone Somalia South Afr...

Lo stesso argomento in dettaglio: Imperatori romani e Imperatori bizantini. Questo è un elenco delle donne che furono consorti dell'imperatore romano, il sovrano dell'impero romano. I Romani non avevano nessun singolo termine per la posizione: furono utilizzati il titolo latino di augusta (derivato dal titolo onorifico conferito al Ottaviano). Nel III secolo, la moglie dell'imperatore poteva anche ricevere i titoli di mater castrorum (madre degli accampamenti) e mater patriae (madre...

Battaglia di Manilaparte della campagna delle Filippine della seconda guerra mondialeFotografia aerea della città di Manila devastata, maggio 1945Data3 febbraio - 3 marzo 1945 LuogoManila, Filippine EsitoVittoria alleata Schieramenti Stati Uniti Commonwealth delle Filippine Giappone Comandanti Douglas MacArthur Oscar Griswold Robert S. Beightler Joseph May Swing Emmanuel OcampoTomoyuki YamashitaSanji Iwabuchi† Effettivi35 000 soldati statunitensi3 000 guerriglieri filippini1...















