Джоанна Мерлін

Джоанна Мерлін
англ. Joanna Merlin
Ім'я при народженніДжоанн Ратнер
Народилася15 липня 1931(1931-07-15)[1][2] Редагувати інформацію у Вікіданих
Чикаго, Іллінойс, США
Померла15 жовтня 2023(2023-10-15)[3] (92 роки) Редагувати інформацію у Вікіданих
Лос-Анджелес, Каліфорнія, США[3] Редагувати інформацію у Вікіданих
Громадянство США Редагувати інформацію у Вікіданих
Діяльністьтелеакторка, кіноакторка, кастинг-директор, акторка театру Редагувати інформацію у Вікіданих
Alma materКаліфорнійський університет в Лос-Анджелесі Редагувати інформацію у Вікіданих
ЗакладШкола мистецтв Тіша Редагувати інформацію у Вікіданих
Роки діяльності1956 — 2017
У шлюбі зMartin Lubnerd Редагувати інформацію у Вікіданих
IMDbID 0581008

Джоанн Ратнер, пізніше Мерлін (англ. Joanna Merlin; 15 липня 1931 — 15 жовтня 2023) — американська акторка та кастинг-директорка.

Біографія

Джоанн Ратнер, яка пізніше взяла дошлюбне прізвище своєї матері, народилася в Чикаго, штат Іллінойс. Мати — Тоні Мерлін, батько — Гаррі Ратнер, бакалійник. Уперше виступила на сцені в 11 років, в аматорському театрі у виставі «Too Many Marys». Закінчила Каліфорнійський університет у Лос-Анджелесі, а потім навчалася у Михайла Чехова. Уперше з'явилася на екрані у фільмі Сесіля Де Мілля «Десять заповідей» (1956).

Особисте життя

Перший чоловік Мартін Лабнер з 17 грудня 1950 по 1955 рік. Другий чоловік Девід Дретцін з 1 березня 1964 по 26 червня 2006, народила двох дітей.

Фільмографія

Акторка

Кастинг-директорка

Посилання

  1. ↑ SNAC — 2010.
  2. ↑ Internet Broadway Database — 2000.
  3. ↑ а б Evans G. Joanna Merlin Dies: Original ‘Fiddler On The Roof’ Tzeitel, Longtime Judge On ‘Law & Order: SVU’ Was 92 — 2023.

Read other articles:

Pemilihan umum Bupati Labuhanbatu Selatan 2024

Pemilihan umum Bupati Labuhanbatu Selatan 20242020202927 November 2024Kandidat Peta persebaran suara Bupati & Wakil Bupati Labuhanbatu Selatan petahanaEdiminAhmad Padli Tanjung PDI-P Bupati & Wakil Bupati Labuhanbatu Selatan terpilih belum diketahui Pemilihan umum Bupati Labuhanbatu Selatan 2024 dilaksanakan pada 27 November 2024 untuk memilih Bupati Labuhanbatu Selatan periode 2024-2029.[1] Pemilihan Bupati (Pilbup) Labuhanbatu Selatan tahun tersebut akan diselenggarakan set...

 

Первородный грех

Об экономическом термине см. Первородный грех (экономика). ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Ран�...

 

First Congregational Church (Atlanta)

Historic church in Georgia, United States United States historic placeFirst Congregational ChurchU.S. National Register of Historic PlacesAtlanta Landmark Building First Congregational Church (2012)Show map of Downtown AtlantaShow map of AtlantaShow map of GeorgiaShow map of the United StatesLocation105 Courtland St., NE, Atlanta, GeorgiaCoordinates33°45′27″N 84°23′1″W / 33.75750°N 84.38361°W / 33.75750; -84.38361Arealess than one acreBuilt1908 (1908)B...

Ahmadsyah dari Pagaruyung

AhmadsyahRaja Alam MinangkabauBerkuasa1668 – 1674PenerusIndermasyahNama lengkapSultan Ahmadsyah Yang Dipertuan Pagaruyung Raja Alam Ahmadsyah disebut juga dengan Sultan Ahmadsyah adalah raja alam Pagaruyung. Biografi Munculnya nama Sultan Ahmadsyah sebagai Yang Dipertuan Pagaruyung, berdasarkan dari korespondensi surat-menyurat antara seorang regent VOC di Padang, Jacob Pits dengan raja Minangkabau, salah satunya surat tertanggal 9 Oktober 1668 yang ditujukan kepada Sultan Ahmadsyah, Iskand...

 

Lituanie au Concours Eurovision de la chanson 2021

Lituanieau Concours Eurovision 2021 Données clés Pays  Lituanie Chanson Discoteque Interprète The Roop Langue Anglais Sélection nationale Radiodiffuseur LRT Type de sélection Pabandom iš Naujo! 2021 Date 6 février 2021 Concours Eurovision de la chanson 2021 Position en demi-finale 4e (203 points) Position en finale 8e (220 points) 2020 2022 modifier La Lituanie est l'un des trente-neuf pays participants du Concours Eurovision de la chanson 2021, qui se déroule à Rotterdam aux P...

 

Shenyang FC-31

Fifth-generation jet fighter under development by Shenyang Aircraft Corporation This article is missing information about alleged J-35 rename for carrier use. Please expand the article to include this information. Further details may exist on the talk page. (July 2022) FC-31 Gyrfalcon FC-31 prototype at 2014 China International Aviation & Aerospace Exhibition Role Stealth multirole fighterType of aircraft National origin China Manufacturer Shenyang Aircraft Corporation Design group 601 In...

Thyme

Herb This article is about leaves and oils of the thyme plant. For the genus of thyme plants, see Thymus (plant). For the active ingredient in thyme oil, see Thymol. For other uses, see Thyme (disambiguation). ThymeA bundle of thymeFood energy(per 100 g serving)101 kcal (423 kJ)Nutritional value(per 100 g serving)Protein6 gFat1.7 gCarbohydrate24 g Cookbook: Thyme Thyme (/taɪm/) is the herb (dried aerial parts) of some members of the genus Thymus of aromatic...

 

Royal Niger Company

British mercantile company (1879–1900) Central African Company redirects here. For companies in the modern nation, see list of Central African companies. Flag of the Royal Niger Company The Royal Niger Company was a mercantile company chartered by the British government in the nineteenth century. It was formed in 1879 as the United African Company and renamed to National African Company in 1881 and to Royal Niger Company in 1886. In 1929, the company became part of the United Africa Company...

 

Avarsin Castle

Castle in East Azerbaijan Province, Iran Avarsin Castleقلعه آوارسینGeneral informationTypeCastleTown or cityKaleybar CountyCountry IranCoordinates38°59′21″N 47°3′51″E / 38.98917°N 47.06417°E / 38.98917; 47.06417Avarsin Castle (Persian: قلعه آوارسین) is a historical castle located in Kaleybar County in East Azerbaijan Province, The longevity of this fortress dates back to the 1st millennium BC.[1][2] References ^ قلع�...

نادي إكسلسيور

نادي إكسلسيور تأسس عام 23 يوليو 1902  البلد هولندا  الدوري الدوري الهولندي الممتاز  المدرب مارينوس ديخوزن (29 يناير 2020–)[1]  الموقع الرسمي الموقع الرسمي  تعديل مصدري - تعديل   نادي إكسلسيور هو نادي كرة قدم هولندي تأسس عام 1902، ملعب الفريق هو ملعب فودشتاين وهو أ�...

 

Puncak Burung Nasar

GijjhakutaPuncak Burung NasarPuncak Burung Nasar dari atasTitik tertinggiKoordinat25°00′06.0798″N 85°26′47.3022″E / 25.001688833°N 85.446472833°E / 25.001688833; 85.446472833Koordinat: 25°00′06.0798″N 85°26′47.3022″E / 25.001688833°N 85.446472833°E / 25.001688833; 85.446472833 GeografiGijjhakutaPegununganPerbukitan Rajgir Wikimedia Commons memiliki media mengenai Vulture Peak. Puncak Burung Nasar (Pali: Gijjhakuta, ...

 

2022–23 Scottish Premiership

117th season of top-tier football league in Scotland Football league seasonScottish PremiershipSeason2022–23Dates30 July 2022 – 28 May 2023ChampionsCeltic9th Premiership title53rd Scottish titleRelegatedDundee UnitedChampions LeagueCelticRangersEuropa LeagueAberdeenEuropa Conference LeagueHeart of MidlothianHibernianMatches played228Goals scored670 (2.94 per match)Top goalscorerKyogo Furuhashi(27 goals)Biggest home winHibernian 6–0 Aberdeen(28 January 2023)Biggest away winDundee Un...

Ma (negative space)

Japanese artistic concept Left panel of the Pine Trees Screen (松林図 屏風, Shōrin-zu byōbu) by Hasegawa Tōhaku. The empty space in this piece is considered to be as important as the trees depicted. Ma (間, lit. 'gap, space, pause') is a Japanese reading of a Sino-Japanese character, which is often used to refer to what is claimed to be a specific Japanese concept of negative space.[1][2][3][4] In modern interpretations of traditional Japanese ar...

 

Dreams from My Father

Book by Barack Obama Dreams from My Father AuthorBarack ObamaLanguageEnglishSubjectEarly life of Barack ObamaGenreMemoirPublisherTimes Books (1995)Three Rivers Press (2004)Publication dateJuly 18, 1995August 10, 2004Publication placeUnited StatesMedia typeBookPages403 (1995)442 (2004)ISBN1-4000-8277-3Dewey Decimal973/.0405967625009/0092 B 22LC ClassE185.97.O23 A3 2004 This article is part of a series aboutBarack Obama Pre-presidency Early life and career Illinois State Senator 2004 ...

 

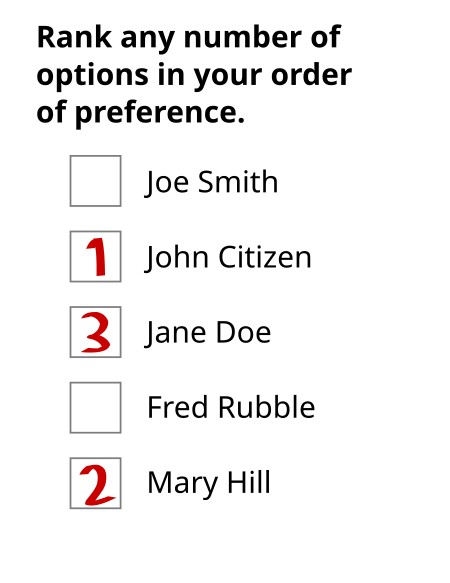
Optional preferential voting

Type of preferential voting system Example of an optional preferential ballot paper One of the ways in which ranked voting systems vary is whether an individual vote must express a minimum number of preferences to avoid being considered invalid (spoiled or informal). Possibilities are: Full preferential voting (FPV) requires all candidates to be ranked Optional preferential voting (OPV) requires only one candidate, the voter's first preference, to be indicated Semi-optional preferential votin...

ميل كريك (فيرجينيا الغربية)

  لمعانٍ أخرى، طالع ميل كريك (توضيح). ميل كريك   الإحداثيات 38°43′54″N 79°58′20″W / 38.73167°N 79.97222°W / 38.73167; -79.97222   [1] تقسيم إداري  البلد الولايات المتحدة[2]  التقسيم الأعلى مقاطعة راندولف  خصائص جغرافية  المساحة 1.182431 كيلومتر مربع1.182429 كيلومتر م...

 

Electoral district of Willyama

Former state electoral district of New South Wales, Australia Willyama was an electoral district for the Legislative Assembly in the Australian State of New South Wales named after the original aboriginal name for the Broken Hill area. It included southern Broken Hill and sparsely occupied areas further south. Since 1904 all of the town was in the district of Broken Hill, surrounded by the rural district of Sturt. In the 1912 redistribution north Broken Hill was in Sturt, while Willyama was c...

 

United Nations Industrial Development Organization

Specialized agency of the United Nations Lima Declaration redirects here. For the statement of intent to form an American trade bloc, see Declaracion de Lima. UNIDO redirects here. For the 1980–1987 Philippine opposition party, see United Nationalist Democratic Organization. United Nations Industrial Development OrganizationAbbreviationUNIDOFormation17 November 1966; 57 years ago (1966-11-17)TypeUnited Nations specialized agencyLegal statusActiveHeadquartersVienna, Austria...

ألفريد غيوم

ألفريد غيوم معلومات شخصية الميلاد 1888إدمونتون  [لغات أخرى]‏  الوفاة نوفمبر 30, 1965 مواطنة المملكة المتحدة المملكة المتحدة لبريطانيا العظمى وأيرلندا (–12 أبريل 1927)  عضو في مجمع اللغة العربية بدمشق  الحياة العملية المدرسة الأم جامعة أكسفورد  المهنة مستعرب،  ...

 

Steiner inellipse

Unique ellipse tangent to all 3 midpoints of a given triangle's sides The Steiner Inellipse. According to Marden's theorem, given the triangle with vertices (1, 7), (7, 5), (3, 1), the foci of the inellipse are (3, 5) and (13/3, 11/3), since D x ( 1 + 7 i − x ) ( 7 + 5 i − x ) ( 3 + i − x ) = − 3 ( 13 3 + 11 3 i − x ) ( 3 + 5 i − x ) {\displaystyle {\begin{aligned}&D_{x}(1+7i-x)(7+5i-x)(3+i-x)\\&=-3\left({\tfrac {13}{3}}+{\tfrac {11}{3}}i-x\ri...