Формула Борда-Карно
|
Read other articles:

Panca InderaAlbum studio karya CokelatDirilis18 Juni 2008Genre Pop rok hard rock Durasi42:47LabelSony BMG Music IndonesiaProduserJan Djuhana dan CokelatKronologi Cokelat Untukmu Indonesiaku (2006)Untukmu Indonesiaku2006 Panca Indera (2008) #Like! (2016) Singel dalam album Panca Indera Salah Bukan Hari Ini Pinjam Hatimu #Like!2016 Panca Indera adalah album studio kelima dari grup musik rok Indonesia Cokelat yang dirilis pada 18 Juni 2008.[1] Berisi 12 lagu dengan hits andalan Salah...

Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2024. Lomen dari Hedysarum hedysaroides Jiring atau Lomen (atau lomentum ) adalah s...

Don Ameche pada tahun 1964 Don Ameche (31 Mey 1908 - 6 Desember 1993) adalah seorang aktor yang populer pada tahun 1930-an dan 1940-an.[1] Ia juga populer sebagai penyiar radio pada zamannya.[1] Ia memulai debutnya dalam film melalui film pendek Beauty at the World's Fair (1933).[1] Setelah itu, ia pindah ke Hollywood untuk melakukan tes di studio MGM.[1] Akan tetapi, MGM menolaknya. Lalu, pada tahun 1935 ia berhasil mendapatkan peran kecil di Clive of India da...

Tyne and Wear Metro station in North Tyneside West MonkseatonTyne and Wear Metro stationGeneral informationLocationMonkseaton, North TynesideEnglandCoordinates55°02′26″N 1°28′34″W / 55.0405469°N 1.4759796°W / 55.0405469; -1.4759796Grid referenceNZ336719Transit authorityTyne and Wear PTEPlatforms2Tracks2ConstructionBicycle facilities 3 cycle lockers 5 cycle pods AccessibleStep-free access to platformOther informationStation codeWMNFare zoneCHistoryOriginal ...

Character from Marvel Comics Comics character Victor ManchaVictor Mancha, surrounded by bars of metal and electricity on the cover of Runaways vol. 2 #22 (2007). Cover art by Jo Chen.Publication informationPublisherMarvel ComicsFirst appearanceRunaways vol. 2 #1 (April 2005)Created byBrian K. Vaughan Adrian AlphonaIn-story informationAlter egoVictor ManchaTeam affiliationsRunawaysAvengers A.I.AbilitiesSuperhuman strength and speed High intelligencePhotographic memory Electromagnetic manipulat...

Italian cookbook first published in 1950 Il cucchiaio d'argento Cover of the first editionCountryItalyLanguageItalianSubjectCookbookPublisherDomus (original)Phaidon Press (English and international)Publication date1950Published in English2005ISBN9788833331676 (Italian edition)WebsiteOfficial website (Italian edition)Official website (English edition) Il cucchiaio d'argento (Italian: [il kukˈkjaːjo darˈdʒɛnto]), or The Silver Spoon in English, is a major Italian cookbook and ...
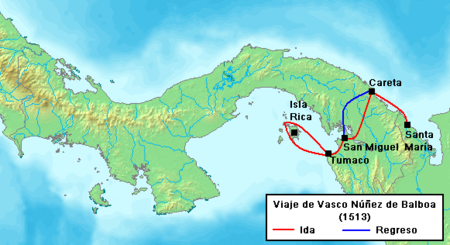
Narrow landstrip in Panama The Isthmus of Panama The Isthmus of Panama (Spanish: Istmo de Panamá), also historically known as the Isthmus of Darien (Istmo de Darién),[1][2] is the narrow strip of land that lies between the Caribbean Sea and the Pacific Ocean, linking North and South America. It contains the country of Panama and the Panama Canal. Like many isthmuses, it is a location of great geopolitical and strategic importance. The isthmus is thought to have been finally ...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...

British general (1729–1814) General Howe redirects here. For other uses, see General Howe (disambiguation). General The Right HonourableThe Viscount HoweKB PCEngraving by Henry Bryan HallCommander-in-Chief of British land forcesIn officeSeptember 1775 – May 1778MonarchGeorge IIIPreceded byThomas GageSucceeded byHenry ClintonMember of Parliamentfor NottinghamIn office1758–1780Serving with Willoughby Aston (1758–1761)Serving with John Plumptre (1761–1774)Serving w...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يوليو 2019) منتخب كينيا لكأس ديفيز البلد كينيا تعديل مصدري - تعديل منتخب كينيا لكأس ديفيز (بالإنجليزية: Kenya Davis Cu...

Face The SunSampul digitalAlbum studio karya SeventeenDirilis27 Mei 2022 (2022-05-27)Durasi29:03BahasaKoreaLabelPledisYG PlusKronologi Seventeen Attacca(2021) Face The Sun(2022) Dream(2022) Singel dalam album Face the Sun Darl+ingDirilis: 15 April 2022 HotDirilis: 27 Mei 2022 Face the Sun adalah album studio keempat dari grup vokal pria Korea Selatan Seventeen. Album ini akan dirilis pada tanggal 27 Mei 2022 oleh Pledis Entertainment melalui YG Plus. Album ini terdiri dari sembilan l...

Para otros usos de este término, véase Guillermo Tell (desambiguación). Guillermo Tell y su hijo. Memorial en Altdorf, capital del cantón suizo de Uri Pourtraits et Vies des Hommes Illustres, 1584. Guillermo Tell (en alemán Wilhelm Tell) es un personaje legendario de la independencia suiza (siglo XIV). No existe ninguna prueba documental contemporánea a la fecha de la existencia de Guillermo Tell que pueda probar que se tratase de un personaje real. Su existencia aparece en una se...

French physicist This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (November 2017) (Learn how and when to remove this message) Henri Abraham in 1935, photo by Studio Harcourt Henri Abraham (1868–1943) was a French physicist who made important contributions to the science of radio waves. He performed some of the first measurements of the propagation velocity of...

Anglo-Saxon church in Bradford-on-Avon, UK 51°20′49″N 2°15′14″W / 51.3470°N 2.2538°W / 51.3470; -2.2538 St Laurence's Church, Bradford-on-Avon, seen from the south in 2005 St Laurence's Church, Bradford-on-Avon, Wiltshire, is one of very few surviving Anglo-Saxon churches in England that does not show later medieval alteration or rebuilding. The church is dedicated to St Laurence, and documentary sources suggest it may have been founded by Saint Aldhelm aro...

1998 studio album by MotörheadSnake Bite LoveStudio album by MotörheadReleased10 March 1998Recorded1998[1]StudioThe Valley[1]GenreHeavy metalLength44:53LabelSPV/SteamhammerProducerHoward Benson & Motörhead[1]Motörhead chronology Protect the Innocent(1997) Snake Bite Love(1998) Everything Louder than Everyone Else(1999) Professional ratingsReview scoresSourceRatingAllMusic[2]Rock Hard8/10[3] Snake Bite Love is the fourteenth studio album...

باليستاين الإحداثيات 39°00′13″N 87°36′46″W / 39.003611111111°N 87.612777777778°W / 39.003611111111; -87.612777777778 [1] تاريخ التأسيس 1811 سبب التسمية فلسطين تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة كراوفورد خصائص جغرافية المساحة 0.79 ميل م...

ITF女子世界网球巡回赛(ITF Women's World Tennis Tour),以前也被称作ITF女子巡回赛或者国际网联女子巡回赛(ITF Women's Circuits),[1]是國際網球總會(ITF)為女子職業網球選手設立的職業網球賽事。[2] ITF世界女子网球巡回赛为女子职业网球选手提供入门级和中级职业赛事,并在ITF青少年世界网球巡回赛和国际女子网球协会WTA巡回赛及WTA125巡回赛之间提供职业通道。IT...

Characterization of measurement error Accuracy is the proximity of measurement results to the accepted value; precision is the degree to which repeated (or reproducible) measurements under unchanged conditions show the same results. Accuracy and precision are two measures of observational error. Accuracy is how close a given set of measurements (observations or readings) are to their true value. Precision is how close the measurements are to each other. The International Organization for Stan...

1859 conflict between Sardinia (with France) and Austria Franco-Austrian War redirects here. For other uses, see Franco-Austrian War (disambiguation). Second Italian War of IndependencePart of the wars of Italian unification and the French-Habsburg rivalryNapoleon III at the Battle of Solferino, by Jean-Louis-Ernest Meissonier, oil on canvas, 1863Date26 April – 12 July 1859(2 months, 2 weeks and 2 days)LocationLombardy–Venetia, Piedmont and the Austrian LittoralResult Franc...













