Рівностепенева неперервність
|
Read other articles:

Pteriida Pteria penguin Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Animalia Filum: Mollusca Kelas: Bivalvia Subkelas: Pteriomorphia Ordo: PteriidaNewell, 1965 Famili Lihat teks Sinonim Pterioida Pteriida adalah ordo moluska kerang laut berukuran besar dan sedang. Ordo ini terdiri dari empat keluarga yang masih ada, di antaranya Pteriidae.[1] Daftar Famili[2] Superfamili Ambonychioidea (punah) Famili Alatoconchidae[3] Famili Ambonychiidae Famili Lunulacardiidae Fam...

Chemical compound AlitretinoinClinical dataTrade namesPanretin (gel), Toctino (oral)AHFS/Drugs.comMonographMedlinePlusa601012License data EU EMA: by INN US DailyMed: Alitretinoin Routes ofadministrationTopical, by mouthATC codeD11AH04 (WHO) L01XF02 (WHO)Legal statusLegal status UK: POM (Prescription only) US: ℞-only EU: Rx-only Pharmacokinetic dataProtein bindingHighly bound, no exact figure available[1]MetabolismLiver (CYP3A4-mediat...

Light rail system in the Dallas-Fort Worth Metroplex This article is about the light rail system in Dallas, Texas. For other uses, see Dart (disambiguation). Not to be confused with Dallas Streetcar. Dallas Area Rapid Transit Light RailDART Blue Line train at Akard station in downtown Dallas heading towards Downtown Rowlett stationOverviewOwnerDARTLocaleDallas, TexasTransit typeLight railNumber of lines4Line number Blue Line Red Line Green Line Orange Line Number of stations65Daily ridership7...
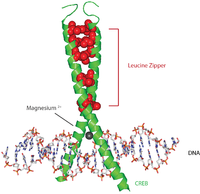
Class of proteins Not to be confused with Clean Renewable Energy Bonds. CREB (top) is a transcription factor capable of binding DNA (bottom) and regulating gene expression. CREB-TF (CREB, cAMP response element-binding protein)[1] is a cellular transcription factor. It binds to certain DNA sequences called cAMP response elements (CRE), thereby increasing or decreasing the transcription of the genes.[2] CREB was first described in 1987 as a cAMP-responsive transcription factor r...

Pour les articles homonymes, voir Thompson. Jacob ThompsonJacob ThompsonFonctionReprésentant des États-UnisBiographieNaissance 15 mai 1810Leasburg (en)Décès 24 mars 1885 (à 74 ans)MemphisNationalité américaineFormation Université de Caroline du Nord à Chapel HillActivité Homme politiqueAutres informationsParti politique Parti démocrateSignaturemodifier - modifier le code - modifier Wikidata Jacob Thompson (15 mai 1810 - 24 mars 1885) était un avocat et un homme politique qui...

Pour les articles homonymes, voir Calmels. Virginie Calmels Fonctions Conseillère régionale de Nouvelle-Aquitaine 4 janvier 2016 – 30 septembre 2020(4 ans, 8 mois et 26 jours) Élection 13 décembre 2015 Président Alain Rousset Groupe politique LR[1] Vice-présidente de Bordeaux Métropole 18 décembre 2015 – 14 février 2019(3 ans, 2 mois et 17 jours) Président Alain Juppé Prédécesseur Josy Reiffers Première adjointe au maire de Bordeaux 4 avril 201...

Katedral ViseuKatedral Santa MariaPortugis: Sé de ViseuKatedral ViseuLokasiViseuNegaraPortugalDenominasiGereja Katolik RomaArsitekturStatusKatedralStatus fungsionalAktifAdministrasiKeuskupanKeuskupan Viseu Katedral Viseu yang bernama lengkap Katedral Santa Matia (Portugis: Sé de Viseu) adalah sebuah gereja katedral Katolik yang terletak di kota Viseu, Portugal. Gereja ini mulai dibangun pada abad ke-12 dan merupakan monumen bersejarah terpenting di kota ini. Saat ini merupakan campu...

Forsythia europaea Status konservasiRisiko rendahIUCN83755828 TaksonomiDivisiTracheophytaSubdivisiSpermatophytesKladAngiospermaeKladmesangiospermsKladeudicotsKladcore eudicotsKladasteridsKladlamiidsOrdoLamialesFamiliOleaceaeTribusForsythieaeGenusForsythiaSpesiesForsythia europaea Degen dan Bald. lbs Forsythia europaea, lebih umum dikenal sebagai forsythia Albania atau forsythia Eropa,[2][3] adalah sebuah spesies tumbuhan berbunga dalam keluarga zaitun, dengan wilayah persebara...

Cricket tournament 2019–20 Ranji Trophy Group AThe Ranji Trophy, awarded to the winnersDates9 December 2019 (2019-12-09) – 15 February 2020 (2020-02-15)Administrator(s)BCCICricket formatFirst-class cricketTournament format(s)Round-robinHost(s) IndiaParticipants9← 2018–19 2019–20 Indian domestic cricket season Men Duleep Trophy Vijay Hazare Trophy (Group A, Group B, Group C, Plate Group) Deodhar Trophy Syed Mushtaq Ali Trophy (Group A, Group B, ...

Pour un article plus général, voir Tour d'Italie 2021. 4e étape du Tour d'Italie 2021 GénéralitésCourse4e étape، Tour d'Italie 2021Type Étape de moyenne montagneDate11 mai 2021Distance187 kmPays ItalieLieu de départPlaisanceLieu d'arrivéeSestolaPartants183Arrivants183Vitesse moyenne37,571 km/hDénivelé1 800 mRésultats de l’étape1er Joe Dombrowski4 h 58 min 38 s(UAE Team Emirates)2e Alessandro De Marchi+ 13 s3e Filippo Fiorelli+ 27 sClassement général à l’issue de l�...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

QriQri in 2017Nama asal이지현LahirLee Ji-hyun12 Desember 1986 (umur 37)Goyang, South KoreaNama lainQriPekerjaanSingeractressKarier musikGenre K-pop R&B Electropop InstrumenVocalsBassTahun aktif2009–sekarangLabelMBK EntertainmentArtis terkait T-ara QBS Korean nameHangul큐리 Alih AksaraKyuriMcCune–ReischauerK'yuriNama lahirHangul이지현 Hanja李智賢 Alih AksaraI Ji-hyeonMcCune–ReischauerYi Chi-hyŏn Lee Ji Hyun (bahasa Korea: 이지현; Lahir 12 Desember, ...

Monument commemorating the independence day of Hargeisa in Somaliland Hargeisa War MemorialA newly rebuilt Hargeisa War Memorial9°33′41″N 44°03′55″E / 9.5615°N 44.0653°E / 9.5615; 44.0653LocationFreedom Square, Independence Avenue, Hargeisa, SomalilandTypeMonumentDedicated toVictims of the indiscriminate aerial bombardment of the city, part of the Isaaq genocide conducted by the Somali dictator Siad Barre[1] The Hargeisa War Memorial (Arabic: �...

Stachyose Identification Nom UICPA (2R,3R,4S,5R,6R)-2-[(2S,3S,4S,5R)-3,4-dihydroxy-2,5-bis(hydroxyméthyl) oxolan-2-yl]oxy-6-[ [(2S,3R,4S,5R,6R)-3,4,5-trihydroxy-6-[ [(2S,3R,4S,5S,6R)-3,4,5-trihydroxy-6-(hydroxyméthyl) oxan-2-yl]oxyméthyl]oxan-2-yl]oxyméthyl]oxane-3,4,5-triol Synonymes D-fructofuranosyl-O-D-galactopyranosyl-(1→6)-O-D-galactopyranosyl-(1→6)-D-glucopyranoside No CAS 470-55-3 No ECHA 100.006.754 No CE 207-427-3 PubChem 91455 SMILES C([C@@H]1[C@H]([C@@H]([C@H]([C@H](O1)OC...
French petroleum engineer and consultant Jean LaherrèreBorn (1931-05-30) 30 May 1931 (age 92)CitizenshipFrenchEducationEcole Polytechnique, École Nationale Supérieure du Pétrole et des MoteursKnown forThe end of cheap oilScientific careerFieldsPetroleum engineerInstitutionsTotal S.A. Jean H. Laherrère (born 30 May 1931) is a French petroleum engineer and consultant,[1] best known as the co-author of an influential 1998 Scientific American article entitled The End of Che...

2016 Japanese filmKanColle: The MovieJapanese nameKanji劇場版 艦これTranscriptionsRevised HepburnGekijō-ban KanKore Directed byKeizō KusakawaWritten byKensuke TanakaJukki HanadaBased onKantai Collectionby DMM.com and Kadokawa GamesProduced bySatoshi MotonagaDaijō KudōStarring Sumire Uesaka Saki Fujita Yuka Iguchi Ayane Sakura Ayana Taketatsu Nao Tōyama Iori Nomizu Rina Hidaka Yumi Tanibe Aya Suzaki CinematographyYasuyuki ItōMusic byNatsumi KameokaProductioncompanyDiomedéaDistribu...

Mixed martial arts promotion based in Russia 2024 in Absolute Championship AkhmatInformationFirst dateJanuary 26, 2024Last dateTBDEventsTotal eventsTBDFightsTotal fightsTBDTitle fightsTBD← 2023 in ACA2025 in ACA → The year 2024 is the 12th year in the history of the Absolute Championship Akhmat, a mixed martial arts promotion based in Russia. 2024 will begin with ACA 169. List of events No. Event Date Venue Location 1 ACA 169: Bibulatov vs. Deák January 26, 2024 Sports ...

William Frazer Baker (1866 – December 4, 1930) was the owner of the Philadelphia Phillies of the National League from 1913 through 1930 and New York City Police Commissioner from 1909 to 1910. William Baker6th New York City Police CommissionerIn officeJuly 1, 1909 – October 20, 1910Appointed byWilliam Jay GaynorPreceded byTheodore A. BinghamSucceeded byJames Church Cropsey Personal detailsBorn1866Pittsburgh, Pennsylvania, U.S.Died(1930-12-04)December 4, 1930Montreal, Quebec, Cana...

Danish footballer (born 1983) Thomas Kahlenberg Kahlenberg training with the Denmark national team in 2014Personal informationFull name Thomas Zeuthen Kahlenberg[1]Date of birth (1983-03-20) 20 March 1983 (age 41)Place of birth Hvidovre, DenmarkHeight 1.83 m (6 ft 0 in)Position(s) Attacking midfielderYouth career1997–1998 Hvidovre1998–2001 BrøndbySenior career*Years Team Apps (Gls)2001–2005 Brøndby 97 (28)2005–2009 Auxerre 130 (19)2009–2013 VfL Wolfsbur...

Unofficial county motto of Sussex, England Village parliament. Postcard posted 1904 We wunt be druv is the unofficial county motto of Sussex in southern England.[1][2] It is a Sussex dialect phrase meaning we will not be driven. The motto asserts that people from the English county of Sussex have minds of their own, and cannot be forced against their will[3] or told what to do.[4] It is used as a motto of the people of Sussex and the Sussex Bonfire Societies.&#...










































![{\displaystyle [a,b]\times [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d2f21b0fe0374437e7e62ac5103dfdef3a9659f)
![{\displaystyle G:C[a,b]\rightarrow C[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8e052394caf0abe29541962f2659b2b6549cb5a)

![{\displaystyle \{G\cdot f\mid \sup \nolimits _{y\in [a,b]}|f(y)|\leqslant 1\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/896792a0550f463a144fb9487c104997f69a80b7)
