Псевдоріманів многовид
|
Read other articles:

Halaman ini berisi artikel tentang pengelompokan seluruh provinsi di timur Manitoba. Untuk pengelompokan Provinsi-Provinsi Maritim dari Newfoundland dan Labrador, lihat Kanada Atlantik. Kanada Timur menurut definisi politik. Kanada Timur (Eastern Canada, Eastern provinces) umumnya dianggap sebagai kawasan dari timur Manitoba, Kanada, yang terdiri dari provinsi berikut ini: New Brunswick Newfoundland and Labrador Nova Scotia Ontario Prince Edward Island Quebec Ontario dan Quebec dimasukkan Kan...

Bagian dari seri artikel mengenaiPerang Sejarah Prasejarah Kuno Abad pertengahan Modern awal Industri Modern Perang generasi keempat Ruang pertempuran Udara Dunia maya Informasi Antariksa Darat Wilayah dingin Gurun Hutan Gunung Perkotaan Bawah tanah Laut Amfibi Biru Cokelat Hijau Permukaan Bawah air Siber Informasi Senjata Lapis baja Artileri Biologi Kavaleri Kimia Konvensional Dunia maya Elektronik Infanteri Nuklir Psikologi Nonkonvensional Taktik Udara Pertempuran Kavaleri Serbuan Serangan ...

Karta med Human Development Index (baserad på 2019 års data,[1] publicerad 15 december 2020.[2]) ≥ 0.900 0.850–0.899 0.800–0.849 0.750–0.799 0.700–0.749 0.650–0.699 0.600–0.649 0.550–0.599 0.500–0.549 0.450–0.499 0.400–0.449 ≤ 0.399 Data ej tillgänglig Human Development Index (HDI) är ett index som används för...

American luxury steamboat (1877–1888) Wide West, probably on the Willamette River. History NameWide West OwnerOregon Steam Navigation Co.; later, Oregon Railway & Navig. Co. RouteColumbia River and lower Willamette River to Portland, Oregon BuilderJohn J. Holland Cost$114,000 Completed1877, Portland, Oregon Out of service1888 Identification80650 FateDismantled 1888, engines and upper works used to complete T. J. Potter NotesHull repowered as propeller-driven barge, wrecked on Destructio...

Swedish politician (born 1957) Eskil ErlandssonMinister for Rural AffairsIn office5 October 2010 – 3 October 2014Prime MinisterFredrik ReinfeldtPreceded byPosition establishedSucceeded bySven-Erik BuchtMinister for AgricultureIn office6 October 2006 – 5 October 2010Prime MinisterFredrik ReinfeldtPreceded byAnn-Christin NyqvistSucceeded byPosition abolishedMember of the Swedish Riksdag for Kronoberg CountyIn office3 October 1994 – 12 March 2019 Personal details...

Asinan Betawi Hidangan Betawi adalah hidangan khas yang berasal dari Suku Betawi. Hidangan Betawi mudah ditemukan di acara-acara tertentu yang diselenggarakan di wilayah DKI Jakarta, Kota Depok, Kabupaten Bekasi dan Kota Bekasi (Jawa Barat) dan Kabupaten Tangerang, Kota Tangerang dan Kota Tangerang Selatan (Banten) seperti pada acara Lebaran Betawi,[1] pernikahan, hari raya Idulfitri, atau di warung-warung tertentu[2] yang menyajikan hidangan khas Betawi. Hidangan ini dipengar...

Pascal Salin nel 2018 Pascal Salin (Parigi, 16 maggio 1939) è un economista francese. Indice 1 Biografia 2 Pensiero 3 Opere 4 Onorificenze 5 Note 6 Collegamenti esterni Biografia Iniziò gli studi iscrivendosi alla Facoltà di giurisprudenza dell'Università di Bordeaux, laureandosi poi in economia all'Istituto di studi politici di Parigi. Dopo il dottorato, conseguì la libera docenza e cominciò a insegnare presso l'Università di Poitiers e l'Università di Nantes. Nel 1969 fu chiamato co...

Сибирский горный козёл Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:СинапсидыКла�...

Venezuelan football player (born 1989) In this Spanish name, the first or paternal surname is Rondan and the second or maternal family name is Giménez. Salomón Rondón Rondón with CSKA Moscow in 2021Personal informationFull name José Salomón Rondón Giménez[1]Date of birth (1989-09-16) 16 September 1989 (age 34)[2]Place of birth Caracas, VenezuelaHeight 1.86 m (6 ft 1 in)[3]Position(s) StrikerTeam informationCurrent team PachucaNumber ...
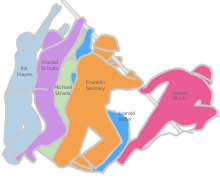
Ira Hamilton Hayes Ira Hamilton Hayes (Sacaton, 12 gennaio 1923 – Bapchule, 24 gennaio 1955) è stato un militare nativo americano. Era un Akimel O'odham, (nativo americano Pima) appartenente alla Comunità Indiana del fiume Gila. Fu un veterano della seconda guerra mondiale nella battaglia di Iwo Jima e la sua notorietà deriva dal fatto di essere stato immortalato, con altri fanti di marina, nella fotografia iconica che ritrae un gruppo di soldati intenti a innalzare la bandiera statunite...

هذه المقالة عن المجموعة العرقية الأتراك وليس عن من يحملون جنسية الجمهورية التركية أتراكTürkler (بالتركية) التعداد الكليالتعداد 70~83 مليون نسمةمناطق الوجود المميزةالبلد القائمة ... تركياألمانياسورياالعراقبلغارياالولايات المتحدةفرنساالمملكة المتحدةهولنداالنمساأسترالي�...

Voce principale: Attentato al Pentagono dell'11 settembre 2001. Le teorie del complotto sull'attentato al Pentagono dell'11 settembre 2001 sono una serie di teorie del complotto che sostengono come argomento centrale il fatto che l'attentato al Pentagono dell'11 settembre 2001 sia da imputare a soggetti diversi dal terrorismo islamico. Dopo l'11 settembre sono stati pubblicati diversi saggi, articoli e documentari, spesso con fini commerciali, con lo scopo di discutere ipotetiche incongruenz...

Datis nuperrimeLatin for 'A new dawn' Encyclical of Pope Pius XIISignature date 5 November 1956Number35 of 41 of the pontificateTextIn LatinIn English← Luctuosissimi eventus Fidei donum → Catholicism portal Datis nuperrime is an encyclical of Pope Pius XII dated 5 November 1956 concerning the Soviet invasion of Hungary to suppress the Hungarian Revolution of 1956. This is a second encyclical protesting the oppression of the Hungarian people. Pope Pius, as in h...

Ancient Greek temple Temple of IsthmiaShown within GreeceLocationKyras Vrysi, Corinthia, GreeceRegionCorinthiaCoordinates37°54′57″N 22°59′35″E / 37.91583°N 22.99306°E / 37.91583; 22.99306TypeSanctuaryLength40.05 mWidth14.018 mHistoryFounded690 to 650 BCAbandoned470 BCPeriodsArchaic GreekSatellite ofIsthmia The Temple of Isthmia is an ancient Greek temple on the Isthmus of Corinth dedicated to the god Poseidon and built in the Archaic Period. ...

2013 Spanish filmJustin and the Knights of ValourSpanish theatrical release posterSpanishJustin y la espada del valor Directed byManuel SiciliaWritten byMatthew JacobsManuel SiciliaStory byManuel SiciliaProduced byMarcelino AlmansaAntonio BanderasKerry FultonRalph KampSergio PablosStarringFreddie HighmoreAntonio BanderasJames CosmoCharles DanceTamsin EgertonRupert EverettBarry HumphriesAlfred MolinaMark StrongDavid WalliamsJulie WaltersOlivia WilliamsSaoirse RonanNarrated byFreddie HighmoreJ...

إي فوتبول النوع لعبة فيديو رياضية المطور(ون) كونامي الناشر(ون) كونامي المِنصّة (أو المِنصّات) أندرويد، غيم كيوب، آي أو إس، بلاي ستيشن 1، بلاي ستيشن 2، بلاي ستيشن 3، بلاي ستيشن 4، بلاي ستيشن 5، بلاي ستيشن بورتبل، غيم بوي أدفانس، نينتندو دي أس، نينتندو 3دي أس، وي، ويندوز، ويندوز �...

Questa voce o sezione sugli argomenti politici russi e nobili russi non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Segui i suggerimenti del progetto di riferimento. Ritratto di Aleksandr Grigor'evič Kushelev-Bezborodko, di Franz Krüger, 1850-1851. Conte Aleksandr Grigor'evič Kušelëv-Bezborodko (in russo Александр Григорьеви�...

Zwitserland op de Olympische Spelen Land Zwitserland IOC-landcode SUI NOC Swiss Olympic Association(de) externe link Olympische Winterspelen 1924 in Chamonix Aantal deelnemers 30 Aantal disciplines 7 MedaillesRang: 4 goud2 zilver0 brons1 totaal3 Zwitserland op de Zomerspelen 1896 · 1900 · 1904 · 1908 · 1912 · 1920 · 1924 · 1928 · 1932 · 1936 · 1948 · 1952 · 1956 · 1960 · 1964 · 1968 · 1972 · 1976 · 1980 · 1984 · 1988 · 1992 · 1996 · 2000 · 2004 · 2008 · 2012 �...

Pour l’article ayant un titre homophone, voir Arjil. « Argile (matériau) » et « Argile (roche) » redirigent ici. Pour les autres significations, voir Argile (homonymie). Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (juillet 2021). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compl...

University in Germany This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: University of Würzburg – news · newspapers · books · scholar · JSTOR (January 2017) (Learn how and when to remove this message) University of WürzburgJulius-Maximilians-Universität WürzburgSeal of the Julius Maximilian University of W...



















