Read other articles:

Aby Nursetyanto Kadiklatsusjatrans Lemdiklat Polri Informasi pribadiLahir15 Oktober 1970 (umur 53)Kepanjen, MalangAlma materAkademi Kepolisian (1992)Karier militerPihak IndonesiaDinas/cabang Kepolisian Negara Republik IndonesiaMasa dinas1992—sekarangPangkat Brigadir Jenderal PolisiSatuanIntelSunting kotak info • L • B Brigjen. Pol. Aby Nursetyanto, S.H., S.I.K. (lahir 15 Oktober 1970) adalah seorang perwira tinggi Polri yang sejak 17 Juli 2020 mengemban amanat s...

Chronologies Données clés 1825 1826 1827  1828  1829 1830 1831Décennies :1790 1800 1810  1820  1830 1840 1850Siècles :XVIIe XVIIIe  XIXe  XXe XXIeMillénaires :-Ier Ier  IIe  IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, République centrafricaine, Comores, République du Congo, République démocratique du Congo, Côte d'Ivoire, Djibouti, Égyp...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Januari 2023. AcamarachiPiliTitik tertinggiKetinggian6.046 m (19.836 ft)Puncak1.608 m (5.276 ft)Masuk dalam daftarUltraKoordinat23°18′S 67°37′W / 23.300°S 67.617°W / -23.300; -67.617Koordinat: 23°18′S 67°37′W...

Kepulauan Spratly Kepulauan Spratly Kepulauan Spratly atau Kepulauan Nansha (Hanzi: 南沙群岛; Pinyin: Nánshā qúndǎo, bahasa Tagalog: Kapuluan ng Kalayaan, bahasa Vietnam: Quần đảo Trường Sa) adalah gugus kepulauan di Laut Tiongkok Selatan yang dipersengketakan beberapa negara di sekitarnya. Terdiri dari beberapa pulau, pulau kecil, ngarai,[1] dan lebih dari 100 terumbu, kadang-kadang dikelompokkan dalam atol tua yang terendam;[2] kepulauan ini t...

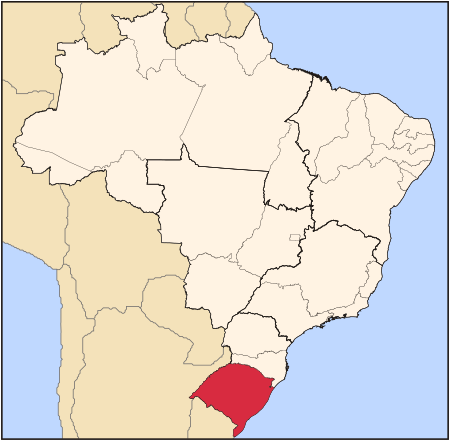
Town in Rio Grande do Sul, Brazil Municipality in South, BrazilGramadoMunicipalityMunicipality of Gramado FlagSealNickname: Hydrangeas' GardenLocation in Rio Grande do SulCoordinates: 29°24′17″S 50°52′35″W / 29.40472°S 50.87639°W / -29.40472; -50.87639Country BrazilRegionSouthState Rio Grande do SulFounded15 December 1954Government • MayorNestor Tissot (PP)Area[1] • Total237 km2 (92 sq mi)Elevati...

For the 1986 TV series, see Sinhá Moça (1986 TV series). Brazilian TV series or program Sinhá MoçaAlso known asLittle MissyGenreTelenovelaCreated byBenedito Ruy BarbosaBased onSinhá MoçaDirected by Ricardo Waddington Rogério Gomes Starring Débora Falabella Danton Mello Osmar Prado Patrícia Pillar Cris Vianna Celso Frateschi Milton Gonçalves Zezé Motta Opening themeSinhá Moçaby LeonardoCountry of originBrazilOriginal languagePortugueseNo. of episodes185ProductionRunning time50 min...

American college football season 2003 Kansas Jayhawks footballTangerine Bowl, L 26–56 vs. NC StateConferenceBig 12 ConferenceDivisionNorthRecord6–7 (3–5 Big 12)Head coachMark Mangino (2nd season)Offensive coordinatorNick Quartaro (2nd season)Defensive coordinatorBill Young (2nd season)Home stadiumMemorial Stadium(Capacity: 50,071)Seasons← 20022004 → 2003 Big 12 Conference football standings vte Conf Overall Team   W   L     W...

Perfect World Publikasi July 2005 December 2006 February 2007 March 2007 May 2007 Malaysia EN September 2007 May 2007 *OB August 2007 *CBT TBA August 2008 Fall 2008 Q3/2008GenreFantasy MMORPGModel bisnisFree-to-play Karakteristik teknisPlatformWindows Modepermainan video multipemain Formatcakram digital Metode inputpapan tombol komputer Format kode Daftar 30 Informasi pengembangPengembangBeijing Perfect WorldPenerbit Beijing Perfect World GF Station Quang Minh MK-Style Cubinet InteractiveTemp...

Elections to the Baseball Hall of Fame This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 1993 Baseball Hall of Fame balloting – news · newspapers · books · scholar · JSTOR (October 2019) (Learn how and when to remove this message) 1993 Baseball Hall of Fame ballotingNew inductees1via BBWAA1Total inductees216In...

Voce principale: Joensuu Wolves. Joensuu Wolves 2013Stagione 2013Sport football americano StadioKoilispuiston Tekonurmi RisultatiN1DSecondo posto Record (V-S-P)5-3-0 Play-offFinale 3DTerzo posto Record (V-S-P)1-2-1 Play-offNon conosciuta Cronologia delle stagioni 2012 2014 Questa voce raccoglie le informazioni riguardanti gli Joensuu Wolves nelle competizioni ufficiali della stagione 2013. Indice 1 Maschile 1.1 III-divisioona 2013 1.1.1 Stagione regolare 1.1.2 Playoff 1.2 Statistiche di squa...

WorthingNama lengkapWorthing Football ClubJulukanThe Rebels, The Mackerel MenBerdiri1886; 137 tahun lalu (1886) (Sebagai Worthing AFC)StadionWoodside Road, Worthing(Kapasitas: 4,000)PemilikGeorge DowellKetuaPete StoneManajerAdam HinshelwoodLigaLiga Conference Wilayah Selatan Inggris Kostum kandang Kostum tandang Worthing Football Club adalah klub sepakbola asosiasi Inggris yang berbasis di Worthing, West Sussex, saat ini bermain di Liga Isthmian Inggris. Klub bermain di Woodside Road. Se...

Посёлоксовхоза «Красковский» 55°40′50″ с. ш. 38°06′49″ в. д.HGЯO Страна  Россия Субъект Федерации Московская область Муниципальный район Раменский Сельское поселение Вялковское История и география Высота центра 137 м Часовой пояс UTC+3:00 Население Население ↗403[1&...

This article contains wording that promotes the subject through exaggeration of unnoteworthy facts. Please help improve it by removing or replacing such wording. (February 2021) (Learn how and when to remove this message) University in Panama This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: University of Panama – news · newspa...

U.S. House district for Texas TX-25 redirects here. The term may also refer to Texas State Highway 25. Not to be confused with Texas's 25th House of Representatives district. Texas's 25th congressional districtTexas's 25th congressional district since January 3, 2023Representative  Roger WilliamsR–WeatherfordDistribution67.47% urban[1]32.53% ruralPopulation (2022)804,617[2]Median householdincome$73,257[3]Ethnicity58.4% White21.8% Hispanic11.7% Black3.9% Two or m...

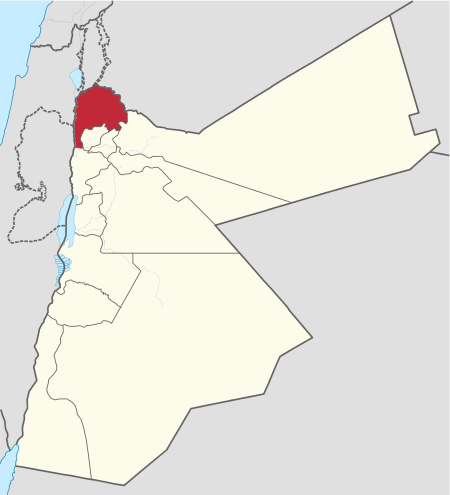
يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) محافظة إربد. تتناول هذه القائمة المواقع الأثرية المسجَّلة رسمياً لدى دائرة الآثار العامة التابعة لوزارة...

Yankee (dibaca Yeng-ki) memiliki beberapa arti yang saling berkaitan, terutama digunakan untuk orang dari Amerika Serikat. Di luar Amerika Serikat, istilah ini secara umum dipakai untuk menyebut orang dari Amerika Serikat. Di dalam negeri Amerika Serikat, istilah Yankee dipakai untuk penduduk dari bagian timur laut Amerika Serikat, atau secara spesifik dipakai untuk orang dari New England yang menunjuk kepada keturunan-keturunan pendatang dari Inggris.[1] Dalam bahasa Indonesia, diken...

Scottish heavy metal band This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The topic of this article may not meet Wikipedia's notability guideline for music. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If notability cannot be shown, the art...

Questa voce sull'argomento canoisti rumeni è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Ivan PatzaichinIvan Patzaichin nel 1990Nazionalità Romania Altezza176 cm Peso79 kg Canoa/kayak Palmarès  Olimpiadi OroCittà del Messico 1968C2 1.000 m OroMonaco di Baviera 1972C1 1.000 m ArgentoMonaco di Baviera 1972C2 1.000 m OroMosca 1980C2 1.000 m ArgentoMosca 1980C2 500 m OroLos Angeles 1984C2 1.000 m ArgentoLos Ang...

コマンダンテ 2021年（左から安田、石井）メンバー 安田 邦祐石井 輝明結成年 2008年解散年 2023年5月2日事務所 吉本興業活動時期 2008年7月 - 2023年5月2日出身 NSC大阪校29期出会い NSC旧コンビ名 ジンクス、ギター（石井）ロマリオ（安田）現在の活動状況 解散安田 : GAG石井 : ピン芸種 漫才、コントネタ作成者 石井輝明過去の代表番組 もってる!? モテるくんオンスト�...

Plane algebraic curve A lemniscate of Bernoulli and its two foci F1 and F2 The lemniscate of Bernoulli is the pedal curve of a rectangular hyperbola Sinusoidal spirals (rn = –1n cos(nθ), θ = π/2) in polar coordinates and their equivalents in rectangular coordinates:   n = −2: Equilateral hyperbola   n = −1: Line   n = −1/2: Parabola   n = 1/2: Cardioid   n = 1: Circle   n = 2: Lemniscate of Bernoulli In geometry, the lemni...