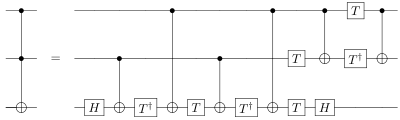
–Т–µ–љ—В–Є–ї—М –Ґ–Њ—Д—Д–Њ–ї—Ц
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

–Ъ–≤—Ц—В–Ї–Њ–љ—Ц–ґ–Ї–∞ –С—Г–і–Њ–≤–∞ –Ї–≤—Ц—В–Ї–Є –Ъ–≤—Ц—В–Ї–Њ–љ—Ц–ґ–Ї–∞ (–ї–∞—В. pedicellus) вАФ —А–Њ–Ј–≥–∞–ї—Г–ґ–µ–љ–љ—П —Б—В–µ–±–ї–∞ –∞–±–Њ –±—Ц—З–љ–Є–є –Ї–≤—Ц—В–Ї–Њ–љ–Њ—Б–љ–Є–є –њ–∞–≥—Ц–љ (—П–Ї–Є–є —А–Њ–Ј–≤–Є–≤–∞—Ф—В—М—Б—П —Г –њ–∞–Ј—Г—Б—Ц –ї–Є—Б—В–Ї–∞); —З–∞—Б—В–Є–љ–∞ –Ї–≤—Ц—В–Ї–Њ–љ–Њ—Б–∞ —Г —Б—Г—Ж–≤—Ц—В—В—Ц, —Й–Њ –љ–µ—Б–µ –љ–∞ —Б–Њ–±—Ц –њ–Њ–Њ–і–Є–љ–Њ–Ї—Г –Ї–≤—Ц—В–Ї—Г[1]. –С—Ц–ї—М—И–µ –∞–±–Њ –Љ–µ–љ—И–µ –≤—Ц–і—А—Ц–Ј–љ—П—Ф—В—М—Б—П –≤—Ц–і —В–Є—Е —З–∞—Б—В–Є–љ —Б—В–µ–±–ї–∞, —Й–Њ пњљ...

Ushuaia International AirportAeropuerto Internacional de UshuaiaIATA: USHICAO: SAWH USHLocation of airport in Tierra del FuegoInformasiJenisPublicPengelolaCivil Aviation AdministrationLokasiUshuaia, Tierra del Fuego, ArgentinaKetinggian dpl31 mdplKoordinat54¬∞50вА≤36вА≥S 068¬∞17вА≤44вА≥W / 54.84333¬∞S 68.29556¬∞W / -54.84333; -68.29556Situs webtierradelfuego.org.ar/...Landasan pacu Arah Panjang Permukaan m kaki 07/25 3,030 9,941 Beton Sources: Argentinian AIP...
Ellerau Lambang kebesaranLetak Ellerau di Segeberg NegaraJermanNegara bagianSchleswig-HolsteinKreisSegeberg Pemerintahan вАҐ MayorBernd ExlerLuas вАҐ Total7,09 km2 (274 sq mi)Ketinggian24 m (79 ft)Populasi (2013-12-31)[1] вАҐ Total5.911 вАҐ Kepadatan8,3/km2 (22/sq mi)Zona waktuWET/WMPET (UTC+1/+2)Kode pos25479Kode area telepon04106Pelat kendaraanSESitus webwww.ellerau.de Ellerau adalah kota yang terletak di dis...

Wanita yang menggambarkan kondisi distres Amal menghilangkan stres dari seorang ibu yang kelebihan beban. Dalam kedokteran, distres adalah keadaan aversif di mana seseorang tidak dapat sepenuhnya beradaptasi dengan stresor dan stres yang diakibatkannya lalu menunjukkan perilaku maladaptif.[1] Hal ini dapat terlihat dengan adanya berbagai fenomena, seperti interaksi sosial inaprosiasi (misalnya, agresi, pasivitas, atau penarikan diri). Distres adalah kebalikan dari eustres, stres posit...

Family of software products This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Turbo software вАУ news ¬Ј newspapers ¬Ј books ¬Ј scholar ¬Ј JSTOR (February 2019) (Learn how and when to remove this template message) TurboLogo of the company. Although it reads turbo.net, the company uses it to represent itself and...

Rita Sheba (lahir Sinarita Sheba Kairupan; 24 Maret 1961) adalah seorang aktris, model, penyanyi, dan pengusaha berkebangsaan Indonesia. Rita ShebaLahirSinarita Sheba Kairupan24 Maret 1961 (umur 63)Semarang, Jawa Tengah, IndonesiaKebangsaanIndonesiaPekerjaanAktrismodelpenyanyipengusahaTahun aktif1985вАУ1993Anak4 Kehidupan awal Sinarita Sheba Kairupan dilahirkan pada tanggal 24 Maret 1961, di Semarang, Jawa Tengah, sebagai putri bungsu dari lima bersaudara pasangan H.H Kairupan dan P...

Province of Ecuador Province in EcuadorAzuayProvinceProvince of Azuay FlagCoat of armsLocation of Azuay in Ecuador.Cantons of Azuay ProvinceCoordinates: 2¬∞53вА≤S 79¬∞00вА≤W / 2.883¬∞S 79.000¬∞W / -2.883; -79.000CountryEcuadorEstablishedJune 25, 1824CapitalCuencaCantons List of Cantons Camilo Ponce Enr√≠quezChordelegCuencaEl PanGir√≥nGuachapalaGualaceoNab√≥nO√±aPautePucaraSan FernandoSanta IsabelSevilla de OroSigsig Government вАҐ Provincial PrefectJuan Crist...

Chasing the DragonPoster filmNama lainTradisionalињљйЊНSederhanaињљйЊЩMandarinZhuƒЂ L√≥ng SutradaraWong Jing Jason KwanProduserWong Jing Donnie Yen Andy Lau Connie Wong Ren Yue Jeffrey Chan Stanley Tong Yang GuangDitulis olehWong JingPemeranDonnie Yen Andy LauPenata musikChan Kwong-wing Patrick LuiSinematograferJason KwanPenyuntingLi Ka-wingPerusahaanproduksiMega-Vision Project Workshop Bona Film Group Company Infinitus Entertainment Super BulletDistributorMega-Vision Project Work...

–Р–Ј–Є–∞—В—Б–Ї–Є–є –±–∞—А—Б—Г–Ї –Э–∞—Г—З–љ–∞—П –Ї–ї–∞—Б—Б–Є—Д–Є–Ї–∞—Ж–Є—П –Ф–Њ–Љ–µ–љ:–≠—Г–Ї–∞—А–Є–Њ—В—Л–¶–∞—А—Б—В–≤–Њ:–Ц–Є–≤–Њ—В–љ—Л–µ–Я–Њ–і—Ж–∞—А—Б—В–≤–Њ:–≠—Г–Љ–µ—В–∞–Ј–Њ–Є–С–µ–Ј —А–∞–љ–≥–∞:–Ф–≤—Г—Б—В–Њ—А–Њ–љ–љ–µ-—Б–Є–Љ–Љ–µ—В—А–Є—З–љ—Л–µ–С–µ–Ј —А–∞–љ–≥–∞:–Т—В–Њ—А–Є—З–љ–Њ—А–Њ—В—Л–µ–Ґ–Є–њ:–•–Њ—А–і–Њ–≤—Л–µ–Я–Њ–і—В–Є–њ:–Я–Њ–Ј–≤–Њ–љ–Њ—З–љ—Л–µ–Ш–љ—Д—А–∞—В–Є–њ:–І–µ–ї—О—Б—В–љ–Њ—А–Њ—В—Л–µ–Э–∞–і–Ї–ї–∞—Б—Б:–І–µ—В–≤–µ—А–Њ–љ–Њ–≥–Є–µ–Ъ–ї–∞–і–∞:–Р–Љ–љ–Є–Њ—В—Л–Ъ–ї–∞–і–∞:–°–Є–љ–∞–њ—Б–Є–і—Л–Ъ–ї–∞—Б—Б:–Ь–ї–µпњљ...

B√≥ng ch√†yC∆° quan quбЇ£n l√љ cao nhбЇ•tWorld Baseball Softball ConfederationThi ƒСбЇ•u lбЇІn ƒСбЇІuN∆∞бїЫc Anh, thбЇњ kбїЈ 18 (tiбїБn th√Ґn)Hoa Kбї≥, thбЇњ kбїЈ 19 (phi√™n bбЇ£n hiбїЗn ƒСбЇ°i)ƒРбЇЈc ƒСiбїГmSбїС th√†nh vi√™n ƒСбЇ•u ƒСбїЩi9H√ђnh thбї©cBat-and-ballTrang bбїЛQuбЇ£ b√≥ng ch√†yGбЇ≠y b√≥ng ch√†yGƒГng tay b√≥ng ch√†yM≈© bбЇ£o hiбїГm (cбїІa cбЇІu thбїІ ph√°t b√≥ng)ƒРбїУ bбЇ£o hбїЩ cбїІa cбЇІu thбїІ bбЇѓt b√≥ngHiбїЗn diбїЗnOlympicThбїГ thao biбїГu ...

еЬЯеЇУжЫЉжЦѓеЭ¶жАїзїЯеЬЯеЇУжЫЉжЦѓеЭ¶еЫљеЊљеЬЯеЇУжЫЉжЦѓеЭ¶жАїзїЯжЧЧзПЊдїїи∞Ґе∞ФиЊЊе∞Ф¬ЈеИЂе∞ФеЊЈз©ЖеУИжҐЕе§Ъе§ЂиЗ™2022еєі3жЬИ19жЧ•еЃШйВЄйШњдїАеУИеЈіеЊЈжАїзїЯеЇЬпЉИOguzkhan Presidential PalaceпЉЙж©ЯйЧЬжЙАеЬ®еЬ∞йШњдїАеУИеЈіеЊЈдїїеСљиАЕзЫіжО•йАЙдЄЊдїїжЬЯ7еєіпЉМеПѓињЮйАЙињЮдїїй¶ЦдїїиР®еЄХе∞Фз©ЖжЛЙзЙє¬Је∞ЉдЇЪдљРе§ЂиЃЊзЂЛ1991еєі10жЬИ27жЧ• еЬЯеЇУжЫЉжЦѓеЭ¶еЬЯеЇУжЫЉжЦѓеЭ¶жФњеЇЬдЄОжФњж≤ї еЫљеЃґжФњеЇЬ еЬЯеЇУжЫЉжЦѓеЭ¶еЃ™ж≥Х еЫљжЧЧ еЫљеЊљ еЫљж≠М зЂЛж≥Хж©ЯйЧЬпЉИиЛ±иѓ≠пЉЪNational Council of TurkmenistanпЉЙ ...

2019 EU copyright reform directive This article is about the 2019 Directive. For the 2001 Directive, see Information Society Directive. Directive 2019/790European Union directiveText with EEA relevanceTitleDirective (EU) 2019/790 of the European Parliament and of the Council of 17 April 2019 on copyright and related rights in the Digital Single Market and amending Directives 96/9/EC and 2001/29/ECMade underArticles 53(1), 62 and 114Journal referenceL 130, 17 May 2019HistoryEuropean Parliament...

2003 album by Smile Empty Soul Smile Empty SoulStudio album by Smile Empty SoulReleasedMay 27, 2003Genre Post-grunge alternative rock alternative metal nu metal[1] Length53:08LabelLavaProducerJohn Lewis ParkerSmile Empty Soul chronology Smile Empty Soul(2003) Anxiety(2005) Singles from Smile Empty Soul Bottom of a BottleReleased: March 25, 2003[2] Nowhere KidsReleased: October 14, 2003 SilhouettesReleased: March 2, 2004 Professional ratingsReview scoresSourceRatingAllmusic...

Pinacoteca comunale Attilio MoroniVeduta di Palazzo Vitelli alla Cannoniera UbicazioneStato Italia Localit√† Porto Recanati IndirizzoCastello Svevo - Piazza F.lli Brancondi, 1 CaratteristicheTipoArcheologiaArte modernaArte contemporanea Modifica dati su Wikidata ¬Ј Manuale La Pinacoteca comunale Attilio Moroni √® il museo comunale di Porto Recanati che conserva nel palazzo del Castello svevo, costruito nella prima met√† del XIII secolo, le collezioni della citt√†. Gran parte de...

British Conservative politician and Governor of New Zealand (1853вАУ1911) For other people named William Onslow, see William Onslow (disambiguation). The Right HonourableThe Earl of OnslowGCMG PC DL11th Governor of New ZealandIn office2 May 1889 вАУ 24 February 1892MonarchVictoriaPremierHarry AtkinsonJohn BallancePreceded bySir William JervoisSucceeded byThe Earl of GlasgowPresident of the Board of AgricultureIn office19 May 1903 вАУ 12 March 1905MonarchEdward VI...

Hauts-de-FranceWilayah PrancisQuai Belu di Amiens BenderaLambang kebesaranKoordinat: 49¬∞55вА≤14вА≥N 2¬∞42вА≤11вА≥E / 49.9206¬∞N 2.7030¬∞E / 49.9206; 2.7030Country PrancisPrefectureLilleDepartments 5 AisneNordOisePas-de-CalaisSomme Pemerintahan вАҐ President of the Regional CouncilXavier Bertrand (LR)Luas вАҐ Total31.813 km2 (12,283 sq mi)Peringkat9thPopulasi (2015 est.) вАҐ Total6.009.976 вАҐ Kepadatan19...
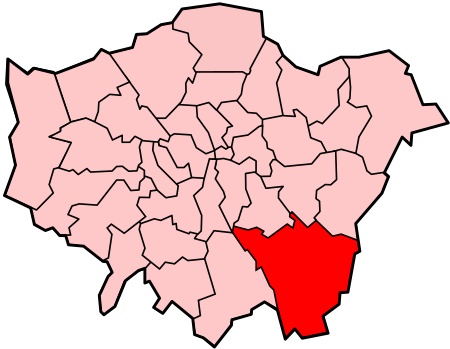
Parliamentary constituency in the United Kingdom, 2010-2024 Lewisham West and PengeFormer borough constituencyfor the House of CommonsBoundary of Lewisham West and Penge in Greater LondonCountyGreater LondonElectorate69,399 (December 2010)[1]Major settlementsForest Hill, Penge and Sydenham2010вАУ2024SeatsOneCreated fromLewisham WestBeckenhamReplaced byBeckenham and PengeLewisham EastLewisham West and East Dulwich Lewisham West and Penge was a constituency in Greater London created in ...

гБУгБЃи®ШдЇЛгБѓж§Ьи®ЉеПѓиГљгБ™еПВиАГжЦЗзМЃгВДеЗЇеЕЄгБМеЕ®гБПз§ЇгБХгВМгБ¶гБДгБ™гБДгБЛгАБдЄНеНБеИЖгБІгБЩгАВеЗЇеЕЄгВТињљеК†гБЧгБ¶и®ШдЇЛгБЃдњ°й†ЉжАІеРСдЄКгБЂгБФеНФеКЫгБПгБ†гБХгБДгАВпЉИгБУгБЃгГЖгГ≥гГЧгГђгГЉгГИгБЃдљњгБДжЦєпЉЙеЗЇеЕЄж§Ь糥?: жЬђеЇДжЧ©з®≤зФ∞йІЕ вАУ гГЛгГ•гГЉгВє ¬Ј жЫЄз±Н ¬Ј гВєгВЂгГ©гГЉ ¬Ј CiNii ¬Ј J-STAGE ¬Ј NDL ¬Ј dlib.jp ¬Ј гВЄгГ£гГСгГ≥гВµгГЉгГБ ¬Ј TWLпЉИ2010еєі12жЬИпЉЙ жЬђеЇДжЧ©з®≤зФ∞йІЕ еМЧеП£пЉИ2006еєі11жЬИпЉЙ гБїгВУгБШгВЗпњљ...

Italian multinational tyre manufacturer Not to be confused with V-Rally. Pirelli & C. S.p.A.Headquarters in Milan, ItalyCompany typePublicTraded asBIT: PIRCISINIT0005278236IndustryAutomotiveFounded28 January 1872; 152 years ago (1872-01-28)Milan, ItalyFounderGiovanni Battista PirelliHeadquartersMilan, Italy 45¬∞31вА≤10вА≥N 9¬∞12вА≤40вА≥E / 45.5195317¬∞N 9.2111299¬∞E / 45.5195317; 9.2111299Area servedWorldwideKey peopleLi Fanrong (Chairman)Mar...

Questa voce sull'argomento stagioni delle societ√† calcistiche italiane √® solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Football Club Union Pro. Societ√† Sportiva G.I.L. MoglianoStagione 1942-1943Sport calcio SquadraFootball Club Union Pro Allenatore Angelo Dell'Antonia Presidente Ildebrando Bonaventura Serie C12¬Ї posto nel girone A. Retrocesso in Prima Divisione, poi riammesso alla c...