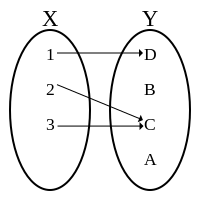
Punsiyon (matematika)
|
Read other articles:

Biografi ini tidak memiliki sumber tepercaya sehingga isinya tidak dapat dipastikan. Bantu memperbaiki artikel ini dengan menambahkan sumber tepercaya. Materi kontroversial atau trivial yang sumbernya tidak memadai atau tidak bisa dipercaya harus segera dihapus.Cari sumber: Rahma Sarita – berita · surat kabar · buku · cendekiawan · JSTOR (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Rahma SaritaLahirRahma Sarita Al-Jufri7 April 19...

Ganjil GenapSutradaraBene Dion RajagukgukProduserManoj PunjabiDitulis oleh Bene Dion Rajagukguk Sigit Sulistyo BerdasarkanGanjil Genapoleh Almira BastariPemeran Clara Bernadeth Oka Antara Baskara Mahendra Penata musikAndhika TriyadiSinematograferPadri NadeakPenyuntingRyan PurwokoPerusahaanproduksiMD PicturesTanggal rilis 28 Juni 2023 (2023-06-28) (Indonesia) Durasi124 menitNegaraIndonesiaBahasaIndonesia Ganjil Genap adalah film drama komedi romantis Indonesia tahun 2023 yang di...

هيلسايد الإحداثيات 41°55′05″N 74°02′00″W / 41.9181°N 74.0333°W / 41.9181; -74.0333 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة أولستر خصائص جغرافية المساحة 2.155999 كيلومتر مربع2.145579 كيلومتر مربع (1 أبريل 2010) ارتفاع 97 متر عدد السكان...
Sevillana UbicaciónCoordenadas 4°35′43″N 74°08′55″O / 4.5951805989402, -74.14849945845Dirección Autopista Sur con carrera 61ALocalidad Kennedy y TunjuelitoCiudad BogotáDatos de la estaciónCódigo TM0096Inauguración 15 de abril de 2006Operador TransMilenioLíneasLínea(s) NQS Sur « Venecia ← G → C.C. Paseo Villa del Río - Madelena » [editar datos en Wikidata] La estación sencilla Sevillana, hace parte del sistema de transporte masivo de Bogotá ...

Fictional broadsheet newspaper This article is about the fictional comic book newspaper. For other uses, see Daily Planet (disambiguation). Daily PlanetPublication informationFirst appearanceAction Comics #23(April 1940)In-story informationType of businessNewspaperOwner(s)Morgan Edge Franklin SternLex LuthorBruce WayneEmployee(s)Perry White (editor-in-chief)Clark KentLois LaneJimmy OlsenCat GrantRon TroupeSteve LombardLana Lang The Daily Planet is a fictional newspaper appearing in American c...

Chemical reaction Prilezhaev reaction Named after Nikolai Alexandrovich Prilezhaev (also spelled Nikolaj Alexandrovich Prileschajew, Russian: Николай Александрович Прилежаев) Reaction type Ring forming reaction Identifiers Organic Chemistry Portal prilezhaev-reaction RSC ontology ID RXNO:0000405 The Prilezhaev reaction, also known as the Prileschajew reaction or Prilezhaev epoxidation, is the chemical reaction of an alkene with a peroxy acid to form epoxides.[...

2006 single by Mobb Deep featuring 50 Cent and Nate DoggHave a PartySingle by Mobb Deep featuring 50 Cent and Nate Doggfrom the album Get Rich or Die Tryin': Music from and Inspired by the Motion Picture & Blood Money ReleasedMarch 2, 2006GenreHip hopLength3:56LabelG-UnitInterscopeSongwriter(s)Curtis JacksonAlbert JohnsonKejuan MuchitaNathaniel Dwayne HaleFarid NassarProducer(s)FredwreckMobb Deep singles chronology Outta Control (Remix)(2005) Have a Party(2006) Put Em in Their Place(2...

Cet article est une ébauche concernant une chanson, le Concours Eurovision de la chanson et le Royaume-Uni. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. I Love the Little Things Chanson de Matt Monro au Concours Eurovision de la chanson 1964 Sortie 1964 Langue Anglais Genre Musique britannique Auteur-compositeur Tony Hatch (en) Chansons représentant le Royaume-Uni au Concours Eurovision de la chan...

Jamaican footballer (born 1991) For the American singer and actress, see Rebecca Spencer (singer). Rebecca Spencer Spencer with Tottenham in 2019Personal informationFull name Rebecca Leigh Spencer[1]Date of birth (1991-02-22) 22 February 1991 (age 33)Place of birth Harrow, London, EnglandHeight 1.67 m (5 ft 6 in)Position(s) GoalkeeperTeam informationCurrent team Tottenham HotspurNumber 22Youth career Watford Ladies2001–2006 ArsenalSenior career*Years Team Apps (G...

Chemical compound FUB-APINACALegal statusLegal status CA: Schedule II DE: NpSG (Industrial and scientific use only) UK: Class B US: Schedule I Identifiers IUPAC name N-(Adamantan-1-yl)-1-[(4-fluorophenyl)methyl]-1H-indazole-3-carboxamide CAS Number2180933-90-6 YPubChem CID118796517ChemSpider30922497UNIIOF9Q7PH4UDChemical and physical dataFormulaC25H26FN3OMolar mass403.501 g·mol−13D model (JSmol)Interactive image SMILES O=C(NC1(C[C@H]2C3)C[C@H]3C[C@H](C2)C1)C4=...

Samsung Galaxy A series adalah sebuah lini ponsel Android kelas awal hingga menengah keatas yang diproduksi oleh Samsung Electronics. Seri Galaxy A mirip dengan seri Samsung Galaxy S, tapi dengan spesifikasi yang lebih rendah dan fitur yang lebih sedikit. Ponsel pertama dalam seri ini adalah Samsung Galaxy Alpha, yang diperkenalkan pada tanggal 13 Agustus 2014. Samsung Galaxy A3 (2015) Pada bulan Desember 2014, 3 bulan sesudah rilis Samsung Galaxy Alpha, Samsung berencana untuk mengakhiri pro...

Zwentibold Zwentibold dans la Historia Welforum (v. 1170). Titre Roi de Lotharingie mai 895 – 30 août 900(5 ans et 3 mois) Prédécesseur Arnulf de Carinthie Successeur Louis IV de Germanie Biographie Dynastie Carolingiens Date de naissance 870 ou 871 Date de décès 13 ou 30 août 900 Lieu de décès Susteren (Lotharingie) Sépulture Abbaye de Susteren Père Arnulf de Carinthie Mère Vinburge(?) Fratrie Ratold d'ItalieLouis IV de Germanie Conjoint Oda de Saxe modifier...

Cet article est une ébauche concernant une localité de la Communauté valencienne. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Tormos Héraldique Vue aérienne du centre du village de Tormos. Administration Pays Espagne Communauté autonome Communauté valencienne Province Province d'Alicante Comarque Marina Alta District judic. Dénia Maire Mandat Vicente Javier Ripoll Pereto (PP) Depuis 2003 Code postal ...

Pour les articles homonymes, voir Robert. Hubert RobertÉlisabeth Vigée Le Brun, Hubert Robert (1788),Paris, musée du Louvre.BiographieNaissance 22 mai 1733Paris (royaume de France)Décès 15 avril 1808 (à 74 ans)Ancien 1er arrondissement de ParisSépulture Cimetière d'AuteuilNationalité françaiseFormation Collège de Navarre (1745-1751)Université de ParisActivités Conservateur de musée, dessinateur, peintre, architectePériode d'activité 1748-1808Autres informationsMembre de ...

Questa voce sull'argomento calciatori cechi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Karel Krejčí Nazionalità Cecoslovacchia Rep. Ceca (dal 1993) Calcio Ruolo Allenatore (ex centrocampista) Squadra Příbram Termine carriera 1º luglio 2000 - giocatore CarrieraSquadre di club1 1989-1993 Viktoria Plzeň? (?)1993-1995 Svit Zlín? (?)1995-1998 Dukla Praga? (?)199...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Tes cepat SARS-CoV-2. Tes aliran lateral deteksi antigen virus Tes cepat antigen COVID-19, juga sering disebut tes aliran lateral COVID-19, adalah tes cepat antigen yang digunakan untuk mendeteksi infeksi SARS-CoV-2 (COVID-19). Tes ini cepat diimplementasikan dengan pelatihan minimal, menawarkan keuntungan biaya yang signifikan, menghabiskan sebagian kecil dari bentuk pengujian COVID-19 lainnya, dan memberikan hasil kepada pengguna dalam 5–30 menit. Namun, mereka memiliki tingkat negatif pa...

Bardsragujn chumb 2002 Competizione Bardsragujn chumb Sport Calcio Edizione 11ª Organizzatore FFA Date dal 13 aprile 2002al 15 novembre 2002 Luogo Armenia Partecipanti 13 Risultati Vincitore P'yownik(5º titolo) Retrocessioni Lori Statistiche Miglior marcatore Arman Karamyan (36 goal) Cronologia della competizione 2001 2003 Manuale Il Bardsragujn chumb 2002 è stato l'undicesima edizione del campionato di calcio armeno, disputato tra il 13 aprile e il 15 novembre 2002 e c...

Luke (Lukáš) of Prague (Czech: Lukáš Pražský, d. December 11, 1528) was a bishop of the Unitas Fratrum, one of the most significant theologians of the Bohemian Reformation. Luke of Prague was born in Prague in the late 1450s and grew up in Prague.[1] He attended University of Prague where he studied the standard church fathers and medieval teachers but was also exposed to the writings of Petr Chelčický.[2] He graduated from the University of Prague on October 2, 1481....

Io sono con teMaria (Nadia Khlifi) in una scena del filmLingua originalearabo e greco antico Paese di produzioneItalia Anno2010 Durata102 min Rapporto2,39:1 Generedrammatico, biblico RegiaGuido Chiesa SoggettoNicoletta Micheli SceneggiaturaNicoletta Micheli, Guido Chiesa, Filippo Kalomenidis ProduttoreSilvia Innocenzi, Giovanni Saulini, Maurizio Totti Casa di produzioneColorado Film, Magda Film, Rai Cinema Distribuzione in italianoBolero Film FotografiaGherardo Gossi MontaggioLuca Gaspari...