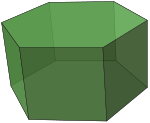
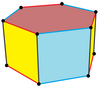
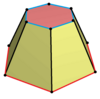
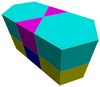
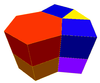
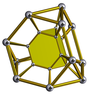
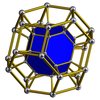
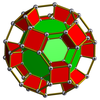
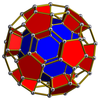
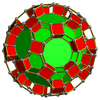
Шестиугольная призма
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Haidar Bagir – berita · surat kabar · buku · cendekiawan · JSTOR Haidar BagirBagir pada 2019LahirHaidarAlmamaterInstitut Teknologi BandungUniversitas HarvardUniversitas IndonesiaPekerjaanUlamaFilantropis...

U.S. House district for Missouri MO-4 redirects here. For soviet subchaser, see MO-class small guard ship. Missouri's 4th congressional districtInteractive map of district boundaries since January 3, 2023Representative Mark AlfordR–Lake WinnebagoPopulation (2022)780,184Median householdincome$62,213[1]Ethnicity83.3% White5.4% Two or more races4.8% Hispanic4.3% Black1.1% Asian1.0% otherCook PVIR+23[2] Missouri's 4th congressional district comprises west-central Missouri....

Election for the Governor of Vermont 1825 Vermont gubernatorial election ← 1824 October 13, 1825 (1825-10-13) 1826 → Nominee Cornelius P. Van Ness Party Democratic-Republican Percentage 100% Governor before election Cornelius P. Van Ness Democratic-Republican Elected Governor Cornelius P. Van Ness Democratic-Republican Elections in Vermont Federal government Presidential elections 1792 1796 1800 1804 1808 1812 1816 1820 1824 1828 1832 1836 1840 1844...

Faten GhattasInformasi pribadiLahir13 Oktober 1964 (umur 59) OlahragaOlahragaRenang Rekam medali Renang putri Mewakili Tunisia Pesta Olahraga Seluruh Afrika 1987 Nairobi gaya punggung 200 m 1987 Nairobi gaya dada 200 m 1987 Nairobi gaya kupu-kupu 100 m 1987 Nairobi gaya kupu-kupu 200 m 1987 Nairobi medley 200 m 1987 Nairobi medley 400 m 1987 Nairobi gaya bebas 100 m 1987 Nairobi gaya bebas 200 m 1987 Nairobi gaya bebas 400 m Faten Ghattas (lahir 13 Oktober 1964) adalah seorang pere...

Paolo SorrentinoSorrentino pada 2008Lahir31 Mei 1970 (umur 53)Naples, ItaliaAlmamaterUniversitas Federico II NaplesPekerjaanSutradara, penulis latarTahun aktif1994–sekarang Paolo Sorrentino (bahasa Italia: [ˈpaːolo sorrenˈtiːno]; kelahiran 31 Mei 1970) adalah seorang sutradara dan penulis latar Italia. Kehidupan dan karier Sorrentino lahir di Naples. Film pertamanya sebagai penulis latar, The Dust of Naples, dirilis pada 1998. Ia juga memulai penyutradaraan film-film pen...

Ramen restaurant chain based in Tokyo, Japan Logo Restaurant interior in Shinjuku, Tokyo, in 2017 Exterior of Afuri in Southwest Portland, Oregon, in 2022 Afuri (also known as Afuri Izakaya)[1] is a chain of ramen restaurants, based in Tokyo, Japan. History The original noodle shop opened at the base of Mount Afuri in 2001. Founder Hiroto Nakamura partnered with Taichi Ishizuki to open a location in southeast Portland's Buckman neighborhood in 2016.[2] Since then, three additi...

Questa voce sugli argomenti federazioni cestistiche e sport a Cipro è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Κυπριακή Ομοσπονδία ΚαλαθόσφαιραςKıbrıs Basketbol FederasyonuDisciplina Pallacanestro Fondazione1966 Nazione Cipro ConfederazioneFIBA (dal 1974)FIBA Europe Sede Nicosia Presidente George Crysostomou Sito ufficialewww.basketball.org.cy/ Modifica dati su Wikidata · Manuale La Federazione cestisti...

Robert Mitchum pada tahun 1949 Robert Charles Durman Mitchum (6 Agustus 1917-1 Juli 1997) merupakan seorang penyanyi dan aktor berkebangsaan Amerika Serikat yang menjadi terkenal pada era 1950-an dan 1960-an. Dia dilahirkan di Bridgeport, Connecticut. Dia berkarier di dunia film sejak tahun 1942 hingga 1996. Filmografi Utama: Saboteur (1942) The Human Comedy (1943) Hoppy Serves a Writ (1943) Aerial Gunner (1943) Border Patrol (1943) Follow the Band (1943) Leather Burners (1943) Colt Comrades ...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

Pour les articles homonymes, voir Tellier. Sébastien Tellier Sébastien Tellier au festival de Dour en 2012.Informations générales Naissance 22 février 1975 (49 ans)Le Plessis-Bouchard, Val-d'Oise ( France) Activité principale Musicien, chanteur Genre musical Musique électronique, Nu-disco Instruments Voix, clavier, piano, guitare, guitare basse, batterie, percussions Labels Record Makers Site officiel www.sebastientellier.com modifier Sébastien Tellier, né le 22 février 1975[1...

Ethnic groups NA‑classThis template is within the scope of WikiProject Ethnic groups, a collaborative effort to improve the coverage of articles relating to ethnic groups, nationalities, and other cultural identities on Wikipedia. If you would like to participate, please visit the project page, where you can join the discussion and see a list of open tasks.Ethnic groupsWikipedia:WikiProject Ethnic groupsTemplate:WikiProject Ethnic groupsEthnic groups articlesNAThis template does not require...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (أبريل 2019) مارغريت أورتيغا معلومات شخصية الميلاد 26 نوفمبر 1993 (31 سنة) مانيلا مواطنة الصين الحياة العملية المهنة مغنية تعديل مصدري - تعديل مارغريت أورتيغ...

Department store in Sydney, Australia Francis Foy redirects here. Not to be confused with Frances Foy. Mark Foy's LimitedThe Mark Foy's buildingTrade nameMark Foy'sCompany typePublicIndustryRetailFoundedSydney, New South Wales 1885; 139 years ago (1885)FounderFrancis Foy, Mark FoyDefunct1980; 44 years ago (1980)FatedefunctHeadquartersSydney, New South Wales, AustraliaServicesDepartment store Mark Foy's Limited or Mark Foy's was a department store in Sydney,...

Newspaper clippings archive Press archives (folders from persons archive, 2015) The 20th Century Press Archives (German: Pressearchiv 20. Jahrhundert) comprises about 19 million of newspaper clippings, organized in folders about persons, companies, wares, events and topics. It originates from the Hamburg Kolonialinstitut (colonial institute) founded in 1908. Within the Hamburg Institute of International Economics (HWWA) it turned into a unique public press archives. In 2007 it was absorbed by...

Dry particulates obscuring clarity of the sky Hazy redirects here. For other uses, see Haze (disambiguation) and Hazy (disambiguation). Part of a series onPollutionHarmattan Haze in Abuja Air Air quality index Atmospheric dispersion modeling Chlorofluorocarbon Combustion Exhaust gas Haze Global dimming Global distillation Indoor air quality Ozone depletion Particulates Persistent organic pollutant Smog Soot Volatile organic compound Waste Biological Biological hazard Genetic Introduced specie...

Localizzazione della Repubblica Centrafricana Le persone LGBT nella Repubblica Centrafricana non sono legalmente perseguite, ma le coppie dello stesso sesso e le famiglie guidate da coppie dello stesso sesso non hanno diritto alle stesse tutele legali disponibili per le coppie formate da individui di sesso opposto. Non esistono protezioni contro la discriminazione basata sull'identita di genere o orientamento sessuale. Indice 1 Leggi sull'attività sessuale tra persone dello stesso sesso 2 Ri...

持続可能エネルギー(英語版) 省エネルギー コジェネレーション 地熱 緑の建築 効率的なエネルギー利用(英語版) エネルギー貯蔵 緑の建築 ヒートポンプ 小型発電(英語版) 再生可能エネルギー 水力 太陽 風力 地熱 バイオマス カーボンニュートラル燃料(英語版) 再生可能エネルギー転換(英語版) 潮力 海洋 持続可能な交通 電気自動車 バイオ燃料 プラグイン...

Municipality in Solothurn, SwitzerlandDornachMunicipality Coat of armsLocation of Dornach DornachShow map of SwitzerlandDornachShow map of Canton of SolothurnCoordinates: 47°29′N 7°37′E / 47.483°N 7.617°E / 47.483; 7.617CountrySwitzerlandCantonSolothurnDistrictDorneckArea[1] • Total5.75 km2 (2.22 sq mi)Elevation338 m (1,109 ft)Population (31 December 2018)[2] • Total6,778 • Densit...

Cet article est une ébauche concernant un aéroport chinois. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Aéroport de Manzhouli Xijiao满洲里西郊机场Mǎnzhōulǐ Xijiāo Jīchǎng Localisation Pays Chine Ville Manzhouli Coordonnées 49° 34′ 00″ nord, 117° 19′ 48″ est Informations aéronautiques Code IATA NZH Code OACI ZBMZ Type d'aéroport Civil Gestionnaire HNA...

هذه المقالة بحاجة لمراجعة خبير مختص في مجالها. يرجى من المختصين في مجالها مراجعتها وتطويرها. (أبريل 2016) إن حيادية وصحة هذه المقالة محلُّ خلافٍ. ناقش هذه المسألة في صفحة نقاش المقالة، ولا تُزِل هذا القالب من غير توافقٍ على ذلك. (نقاش) جزء من سلسلة مقالات حولالشيعة العقيدة توحي...