Функция, имеющая первообразную
|
Read other articles:

China Merchants Bank Company Limited 招商银行股份有限公司JenisPerusahaan publikKode emitenSEHK: 3968 SSE: 600036IndustriPerbankanDidirikan1987KantorpusatShenzhen, Guangdong, Republik Rakyat TiongkokWilayah operasi TiongkokTokohkunciQin Xiao (Ketua)Ma Weihua (Gubernur)ProdukKartu debit multifungsi: Yi Ka Tong; Bank internet disebut Yi Wang Tong; kartu kredit; keuangan korporasi Clickgold; sistem pelayanan Golden Sunflower untuk VIP.JasaDeposito, pinjaman dan jasa bank lainnyaLab...

James Perch Informasi pribadiNama lengkap James Robert PerchTanggal lahir 28 September 1985 (umur 38)Tempat lahir Mansfield, InggrisTinggi 1,80 m (5 ft 11 in) [1]Posisi bermain BekInformasi klubKlub saat ini Wigan AthleticNomor 24Karier junior1996–2004 Nottingham ForestKarier senior*Tahun Tim Tampil (Gol)2004–2010 Nottingham Forest 190 (12)2010–2013 Newcastle United 65 (1)2013– Wigan Athletic 20 (0) * Penampilan dan gol di klub senior hanya dihitung dari l...

Lambang BPN Institut Huygens bertempat di gedung yang sama dengan RKD, Arsip Nasional, Museum Letterkundig Nederlands (LM), Institut Musik Belanda (NMI) dan Koninklijke Bibliotheek. Biografisch Portaal (Inggris: Biography Portalcode: en is deprecated ), atau umumnya disingkat menjadi BPN, adalah sebuah inisiatif yang berbasis di Institut Huygens untuk Sejarah Belanda di Den Haag, dengan tujuan membuat teks biografi di Belanda lebih mudah diakses. Proyek ini dimulai pada bulan Februari 2010 de...

Atari 7800PembuatAtariJenisKonsol permainanGenerasiGenerasi ketigaTanggal rilis21 Mei 1984 (pengumuman)[1] Juni 1984 (rilis awal)[butuh rujukan] Januari 1986 (rilis ulang) 1987Harga perkenalanUS$140Dihentikan1 Januari 1992[butuh rujukan]Terjual3,77 juta unit[2]MediaKartridCPUAtari Sally 6502 (6502C) dengan kecepatan 1,19-1,79 MHzMemoriRAM 4KB, ROM BIOS 4KB, kartrid berkapasitas 48KBTampilan160×240, 320×240 (160×288/320×288 jika PAL), 25 dari 256 warna yang ...

« Ruanda » redirige ici. Pour la colonie formée avec l'actuel Burundi, voir Ruanda-Urundi. République du Rwanda(rw) Repubulika y'u Rwanda (en) Republic of Rwanda (sw) Jamhuri ya Rwanda Drapeau du Rwanda Emblème du Rwanda Devise en kinyarwanda : Ubumwe, Umurimo, Gukunda Igihugu (« Unité, travail, patriotisme ») Hymne en kinyarwanda : Rwanda Nziza (« Notre beau Rwanda ») Fête nationale 4 juillet · Événemen...

Stasiun Sawah Besar B04 Stasiun Sawah Besar bersama kantor pusat PT KAPM (KAI Properti)LokasiJalan Krekot JayaPasar Baru, Sawah Besar, Jakarta Pusat, 10710IndonesiaKoordinat6°9′44″S 106°49′33″E / 6.16222°S 106.82583°E / -6.16222; 106.82583Koordinat: 6°9′44″S 106°49′33″E / 6.16222°S 106.82583°E / -6.16222; 106.82583Ketinggian+15 mOperator KAI Commuter Letakkm 3+836 lintas Jakarta-Manggarai-Bogor/Nambo[1] Jumlah per...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: List of related male and female reproductive organs – news · newspapers · books · scholar · JSTOR (June 2017) (Learn how and when to remove this template message) Tail end of human embryo, from eight and a half to nine weeks old. 1 - 7: Homologous male and fem...

Skirmish with Native Indians 31°25′55″N 87°34′36″W / 31.43181°N 87.57666°W / 31.43181; -87.57666 Canoe FightPart of the Creek WarArtist's impression of the Canoe Fight, from an 1860 biography of Samuel DaleDateNovember 12, 1813LocationAlabama River, Mississippi TerritoryResult United States victoryBelligerents United States CreekCommanders and leaders Samuel Dale unknownStrength 2 war-canoes 1 war-canoeCasualties and losses 1 wounded1 war-canoe damage...

Map all coordinates using OpenStreetMap Download coordinates as: KML GPX (all coordinates) GPX (primary coordinates) GPX (secondary coordinates) The following list includes all of the Canadian Register of Historic Places listings in Nanaimo Regional District, British Columbia. Name Address Coordinates Government recognition (CRHP №) Image A.R. Johnston Block 174 Commercial StreetNanaimo BC 49°10′01″N 123°56′13″W / 49.167°N 123.937°W / 49.167; -123.937&#x...

1999 Tamil film directed by Sundar C. Unnai ThediDirected bySundar CScreenplay bySundar CStory bySundar CProduced by K. Muralidharan V. Swaminathan G. Venugopal Starring Ajith Kumar Malavika CinematographyU. K. Senthil KumarEdited byP. Sai SureshMusic byDevaProductioncompanyLakshmi Movie MakersRelease date 5 February 1999 (1999-02-05) Running time151 minutesCountryIndiaLanguageTamil Unnai Thedi (transl. In search of you) is a 1999 Indian Tamil-language romantic drama film...
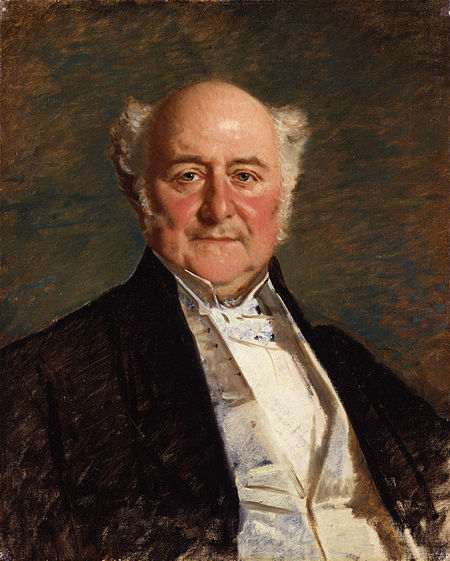
Lord High Chancellor of Great Britain from 1861 to 1865 The Right HonourableThe Lord WestburyPCLord High Chancellor of Great BritainIn office26 June 1861 – 7 July 1865Prime MinisterThe Viscount PalmerstonPreceded byThe Lord CampbellSucceeded byThe Lord Cranworth Personal detailsBorn30 June 1800 (1800-06-30)Bradford on Avon, WiltshireDied20 July 1873 (1873-07-21) (aged 73)Lancaster Gate, LondonNationalityBritishPolitical partyLiberalSpouses Ellinor Abraham ...

جبل التوباد صورة لجبل التوباد الموقع السعودية إحداثيات 22°34′34″N 46°31′26″E / 22.576014°N 46.523838°E / 22.576014; 46.523838 تعديل مصدري - تعديل جبل التوباد، يقع في مدينة الأفلاج التي تقع بدورها إلى الجنوب الغربي من مدينة الرياض بالسعودية بمسافة 350كم.[1] ويقع جبار تحدي�...

Genus of fishes EpinephelusTemporal range: 55–0 Ma PreꞒ Ꞓ O S D C P T J K Pg N Eocene to present[1] Epinephelus fasciatus, the type species Epinephelus tukula Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Actinopterygii Order: Perciformes Family: Serranidae Subfamily: Epinephelinae Tribe: Epinephelini Genus: EpinephelusBloch, 1793 Type species Epinephelus marginalisBloch, 1793[2] Species see text Synonyms[3] Altiserran...

Programme Pioneer Plaque de Pioneer embarquée à bord des deux sondes spatiales Pioneer 10 et Pioneer 11 Données générales Pays États-Unis Agence Armée de terre des États-Unis, National Aeronautics and Space Administration et Space Systems Command (en) Objectifs Exploration spatiale modifier Le programme Pioneer est un programme de la NASA d'exploration du Système solaire à l'aide de sondes spatiales. Entre 1958 et 1978, 19 sondes Pioneer ont été envoyées avec des missions et des...

Kedokteran OlahragaKedokteran Olahraga berperan dalam perawatan dan pencegahan cedera pada atlet.PekerjaanNamaDokterJenis pekerjaanSpesialisSektor kegiatanKedokteranPenggambaranKualifikasi pendidikanSarjana Kedokteran (S.Ked) Profesi Dokter (dr.) Spesialis Kedokteran Olahraga (Sp.KO)Bidang pekerjaanRumah sakit, Klinik Kedokteran olahraga (Bahasa Inggris: Sports medicine), adalah cabang kedokteran yang berhubungan dengan kebugaran fisik, dan pengobatan serta pencegahan cedera yang berhubungan ...

Governor Tim Walz celebrates the signing of House File 100 to legalize recreational cannabis in Minnesota with lawmakers and former governor Jesse Ventura (May 2023) Cannabis in Minnesota is legal for recreational use as of August 1, 2023. On May 30, 2023, Governor Tim Walz signed House File 100 into law, legalizing the use, possession, and cultivation of cannabis within the state.[1] Licenses for commercial sales will likely not be issued until 2025 (with the exception of tribal nat...

Đối với các định nghĩa khác, xem Quỳnh Lưu (định hướng). Bảo tàng chiến khu Quỳnh Lưu Sơ đồ tổng qua chiến khu Quỳnh Lưu Một điểm di tích của Chiến khu Quỳnh Lưu Hồ Đồng Chương ở xã Phú Lộc Bảo tàng chiến khu Quỳnh Lưu Chiến khu Quỳnh Lưu (Vùng ATK Quỳnh Lưu) là một căn cứ cách mạng của Đảng Cộng sản Việt Nam thời kỳ kháng Nhật và Pháp tại Ninh Bình, đồng thời được coi l�...

American actor (born 1968) Billy CrudupCrudup in 2015BornWilliam Gaither Crudup (1968-07-08) July 8, 1968 (age 55)Manhasset, New York, U.S.EducationUniversity of North Carolina, Chapel Hill (BA)New York University (MFA)OccupationActorYears active1989–presentSpouse Naomi Watts (m. 2023)Partner(s)Mary-Louise Parker(1996–2003) Claire Danes(2003–2006)Children1 William Gaither Crudup (/ˈkruːdəp/; born July 8, 1968)[1] is an American actor. ...

Forensic method Examples of blood-spatter and droplet patterns Part of a series onForensic science Physiological Anthropology Biology Bloodstain pattern analysis Dentistry DNA phenotyping DNA profiling Forensic genealogy Entomology Epidemiology Limnology Medicine Palynology Pathology Podiatry Toxicology Social Psychiatry Psychology Psychotherapy Social work Criminalistics Accounting Body identification Chemistry Colorimetry Election forensics Facial reconstruction Fingerprint analysis Firearm...

اليكس مكدونالد معلومات شخصية الميلاد 17 مارس 1948 (العمر 76 سنة)غلاسكو مركز اللعب وسط الجنسية المملكة المتحدة مسيرة الشباب سنوات فريق Luncarty F.C. [الإنجليزية][1] Glasgow United F.C. [الإنجليزية] المسيرة الاحترافية1 سنوات فريق م. (هـ.) 1966–1968 سانت جونستون 65 (17) 1968–1980 رين�...




















![{\displaystyle [-1;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8bc389ca678dffbedd0d41ca0fecb9806c9b7cf)




![{\displaystyle [-a;-1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8df3695e782bf3b655c8dc73ff0a62a9066a12ef)
![{\displaystyle [a;1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54fd9505c957c75307a5cd4ea57fdb4504a42040)






















