Теорема Фейта — Томпсона
|
Read other articles:

Fred Allen nel 1937 Fred Allen, nato John Florence Sullivan (Cambridge, 31 maggio 1894 – New York, 17 marzo 1956), è stato un comico e attore statunitense. Indice 1 Biografia 2 Filmografia parziale 3 Doppiatori italiani 4 Note 5 Voci correlate 6 Altri progetti 7 Collegamenti esterni Biografia Nato in Massachusetts, studiò a Boston. I suoi spettacoli interpretati a Broadway includono The Passing Show of 1922 e The Greenwich Village Follies. Produsse, scrisse e recitò nel programma radiofo...

Artikel biografi ini ditulis menyerupai resume atau daftar riwayat hidup (Curriculum Vitae). Tolong bantu perbaiki agar netral dan ensiklopedis. Ini adalah nama Batak Toba, marganya adalah Sianturi. Bonar Sianturi Bupati SintangMasa jabatan27 Maret 1989 – 5 April 1994GubernurParjoko SuryokusumoAspar Aswin PendahuluDaniel TodingPenggantiAbdillah Kamarullah Informasi pribadiLahir(1944-06-18)18 Juni 1944Sidikalang, Bataklanden, Tapanuli, Hindia BelandaMeninggal22 Mei 2022(2022-05-22) ...

Ordinariat Eropa TimurKatedral Para Martir Kudus, GyumriLokasiNegaraEropa Timur, kecuali Yunani, Polandia dan RumaniaStatistikPopulasi- Katolik(per 2016)618,000Paroki44InformasiRitusRitus ArmeniaPendirian13 Juli 1991KatedralKatedral Para Martir Kudus, GyumriKepemimpinan kiniPausFransiskusPatriarkKrikor Bedros XX GabroyanUskupRaphaël Minassian, I.C.P.BEmeritusNeshan Karakéhéyan, I.C.P.B Ordinariat Eropa Timur adalah sebuah ordinariat (seperempat keuskupan) Gereja Katolik Armenia (Katol...

Archive centre in Cornwall, England Kresen Kernow, Cornwall's archive centre Kresen Kernow (Cornish for Cornwall Centre) in Redruth, United Kingdom is Cornwall's archive centre, home to the world's biggest collection of archive and library material related to Cornwall. Funded by the National Lottery Heritage Fund and Cornwall Council and opened in 2019, it brings together the collections which were previously held at Cornwall Record Office, the Cornish Studies Library and Cornwall and Scilly ...

Duta Besar Indonesia untuk LebanonLambang Kementerian Luar Negeri Republik IndonesiaPetahanaHajriyanto Y. Thoharisejak 7 Januari 2019KantorBeirut, LebanonDitunjuk olehPresiden IndonesiaDibentuk1995[1]Situs webkemlu.go.id/beirut/id Berikut adalah daftar diplomat Indonesia yang pernah menjabat Duta Besar Republik Indonesia untuk Lebanon: No. Foto Nama Mulai menjabat Selesai menjabat Diangkat oleh Ref. Dalindra Aman 1996 Soeharto [2] Syam Soemanagara 2000 2002 ...

Jun Hong LuLu in 2012Nama asal卢军宏Lahir(1959-08-04)4 Agustus 1959Shanghai, TiongkokMeninggal10 November 2021(2021-11-10) (umur 62)Sydney, AustraliaKebangsaanTiongkokAustraliaPendidikan Akademi Teater Shanghai Sekolah Bisnis Universitas New South Wales Pekerjaan Direktur Radio Oriental Australia Pemilik organisasi Guan Yin Citta Dharma Door Dikenal atasPendiri Guan Yin Citta Dharma Door Lu Junhong Hanzi tradisional: 盧軍宏 Hanzi sederhana: 卢军宏 Alih aksara Mandarin - Ha...

Elad beralih ke halaman ini. Untuk kegunaan lain, lihat Elad (disambiguasi). El'ad אלעדTranskripsi bahasa Ibrani • ISO 259ʔelˁad Coat of armsDistrikTengahDidirikan1998Pemerintahan • JenisKota (sejak 2008) • Kepala DaerahIsrael (Srulik) Porush (UTJ)Luas • Total2.756 dunams (2,756 km2 or 1,064 sq mi)Populasi (2009)[1] • Total36.300 • Kepadatan13/km2 (34/sq mi) El'ad...

Pour les articles homonymes, voir Syrmie. Cet article est une ébauche concernant la Serbie et la géographie. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Syrmie (Srem) Administration Pays Serbie Villesou municipalités ŠidInđijaSremska MitrovicaIrigRumaStara PazovaPećinci Démographie Population 311 053 hab. (2011) Densité 89 hab./km2 Géographie Coordonnées 44° 59′ nord, 19...

American politician (1756–1831) Jonathan MasonPortrait of Mason, c. 1850United States Senatorfrom MassachusettsIn officeNovember 14, 1800 – March 3, 1803Preceded byBenjamin GoodhueSucceeded byJohn Quincy AdamsMember of the U.S. House of Representativesfrom Massachusetts's 1st districtIn officeMarch 4, 1817 – May 15, 1820Preceded byArtemas Ward Jr.Succeeded byBenjamin GorhamMember of the Massachusetts SenateIn office1799–1800Member of the Massachusetts House...
Outer garment commonly worn in the Middle Ages in Western Europe The classic knight's surcoat is on the left; the knight on the right has a different style, possibly a jupon Saint Stephen, King of Hungary with a jupon bearing his arms, white and red stripes. Image from the Hungarian Illuminated Chronicle. A surcoat or surcote is an outer garment that was commonly worn in the Middle Ages by soldiers. It was worn over armor to show insignia and help identify what side the soldier was on. In the...

Tokyo Magnitude 8.0東京マグニチュード8.0(Tōkyō Magunichūdo 8.0)Il titolo della serie dalla sigla di testa Generedrammatico Serie TV animeRegiaMasaki Tachibana Composizione serieNatsuko Takahashi Char. designAtsuko Nozaki Dir. artisticaMika Nakajima MusicheKō Ōtani StudioBones, Kinema Citrus ReteFuji TV 1ª TV9 luglio – 19 settembre 2009 Episodi11 (completa) Rapporto16:9 Durata ep.24 min Editore it.Yamato Video Rete it....

American baseball broadcaster Jon SciambiSciambi at Champion Stadium in March 2008BornPhiladelphia, Pennsylvania, U.S.NationalityAmericanAlma materBoston CollegeOccupation(s)Baseball play-by-play announcer, television personalityYears active1993–presentEmployer(s)ESPNMarquee Sports Network Jon Boog Sciambi (/ˈʃɑːmbi/) is an American sportscaster for ESPN and the Marquee Sports Network, and has been the everyday play-by-play announcer for the Chicago Cubs TV broadcasts on Marq...
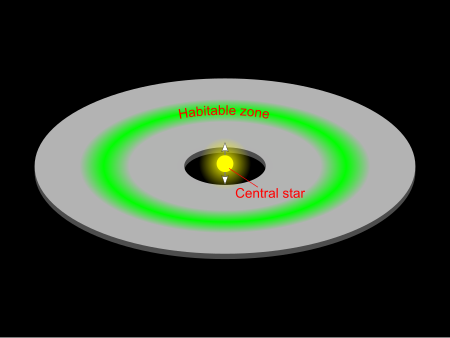
Cet article est une ébauche concernant l’astronautique et la science-fiction. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. L'astroingénierie est, en astronautique, un domaine d'ingénierie visant l'intervention sur des objets célestes (astéroïdes, lunes, planètes, étoiles voire des galaxies entières). Ces procédés sont particulièrement présents en science-fiction, bien que cette discipline soit ...

Parabitacomune Parabita – Veduta LocalizzazioneStato Italia Regione Puglia Provincia Lecce AmministrazioneSindacoStefano Prete (lista civica Lista Agorà) dal 27-5-2019 TerritorioCoordinate40°03′N 18°08′E / 40.05°N 18.133333°E40.05; 18.133333 (Parabita)Coordinate: 40°03′N 18°08′E / 40.05°N 18.133333°E40.05; 18.133333 (Parabita) Altitudine83 m s.l.m. Superficie21,09 km² Abitanti8 757[1] ...

Asinus Kulan Turkmenistan Klasifikasi ilmiah Kerajaan: Animalia Filum: Chordata Kelas: Mammalia Ordo: Perissodactyla Famili: Equidae Genus: Equus Subgenus: Asinus, AJ Decato Spesies Equus africanus Equus hemionus Equus kiang Asinus adalah subgenus dari Equus (hewan berkuku ganjil). Keledai adalah hewan domestikasi yang paling terkenal dari subgenus ini. Terdapat pula beberapa spesies yang hidup liar di Asia dan Afrika. Taksonomi Spesies Equus africanus[1][2] Equus africanus a...

This article is about the events of 1912. For the events of 1791, see Battle of Cape Kaliakra. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Battle of Kaliakra 1912 – news · newspapers · books · scholar · JSTOR (July 2010) (Learn how and when to remove this message) Battle of KaliakraPart of the First...

Hamburg Ravensbrück trialsIn civilian clothing, Ravensbruck Aufseherinnen surrounded by uniformed Allied guards at trial, Hamburg 1947CourtCuriohaus, Hamburg, GermanyStartedDecember 5, 1946 (1946-12-05) (Rotherbaum case)November 5, 1947 (1947-11-05) (Friedrich Opitz case)April 14, 1948 (1948-04-14) (Uckermark trial)and moreDecidedJuly 21, 1948 (1948-07-21) (Rotherbaum case) The first Ravensbrück trial, 1947.[1] The sentenci...

Пам'ятник Тарасові Шевченку у ПразіPomník Tarase Ševčenka v Praze Пам'ятник Тарасу Шевченку у Празі 50°04′42″ пн. ш. 14°24′16″ сх. д. / 50.07844444002777351° пн. ш. 14.40446667002777659° сх. д. / 50.07844444002777351; 14.40446667002777659Координати: 50°04′42″ пн. ш. 14°24′16″ сх. д. / ...

General Motors engine factory in Livonia, Michigan, United States (1971–2010) Livonia Engine was a General Motors engine factory in Livonia, Michigan. It is located at 12200 Middlebelt Rd and opened in 1971. The plant closed in June 2010.[1] Products GM Premium V engine References ^ Carty, Daniel (June 1, 2009). List of GM Plant Closings. CBS News. Retrieved October 21, 2018. vteGeneral Motors assembly plantsUnited StatesCurrent Arlington Bowling Green Detroit/Hamtramck Fairfax Flin...

Private membership organization in New York This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (June 2017) (Learn how and when to remove this message) Larchmont Yacht ClubBurgeeFoundedJune 20, 1880; 144 years ago (1880-06-20)LocationVillage of Larchmont, Westchester County, New YorkWebsitewww.larchmontyc.org Larchmont Yacht Club, 1897, as photog...















