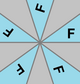
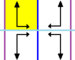
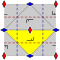
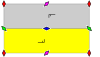
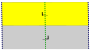
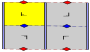
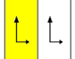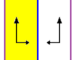Список плоских групп симметрии
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Kiai Adipatie Danoe Radja /Raden Adipati Danoe Redjo / Tumenggung Dipa Nata / Adipati Danu Reja / Syarif Anang Ali Zainal Abidin[1]regent der afdeeling AmonthaijAdipati Danoeradja Tumenggung DipanataBerkuasa1835-9 November 1861PenerusKiai Toemenggoeng Djaija NegaraKelahiranJenal Distrik Amonthaij (Hindia Belanda)Banjar)Kematian9 November 1861 Distrik Amonthaij (Hindia Belanda)WangsaDinasti Banua LimaAyahKiai Ngabehi Jaya Negara (Pambakal Abdul Karim) Bin Datu Kabul[2][3 ...

Indonesia memiliki 98 kota dan kota administrasi. Berdasarkan Peraturan Pemerintah (PP) Nomor 26 Tahun 2008, kota di Indonesia diklasifikasikan menjadi 4 kategori berdasarkan jumlah penduduk, yaitu: kota kecil (sampai dengan 100.000 jiwa), kota sedang (lebih dari 100.000 sampai dengan 500.000 jiwa), kota besar (lebih dari 500.000 sampai dengan 1.000.000), dan kota metropolitan (lebih dari 1.000.000 jiwa).[1] Kota-kota yang masuk dalam artikel ini hanyalah daerah tingkat II yang dikepa...

Basilika Bunda dari KortenbosBasilika Minor Bunda dari KortenbosBelanda: Basiliek Onze-Lieve-Vrouw-Hemelvaartcode: nl is deprecated Basilika Bunda dari KortenbosLokasiSint-TruidenNegaraBelgiaDenominasiGereja Katolik RomaArsitekturStatusBasilika minorStatus fungsionalAktif Basilika Bunda dari Kortenbos (Belanda: Basiliek Onze-Lieve-Vrouw-Hemelvaartcode: nl is deprecated ) adalah sebuah gereja basilika minor Katolik yang terletak di Sint-Truiden, Belgia. Basilika ini ditetapkan statusnya pada 1...

Australian cricketer Bill O'ReillyO'Reilly in the 1930sPersonal informationFull nameWilliam Joseph O'ReillyBorn(1905-12-20)20 December 1905White Cliffs, New South Wales, AustraliaDied6 October 1992(1992-10-06) (aged 86)Sutherland, New South Wales, AustraliaNicknameTigerHeight6 ft 2 in (1.88 m)BattingLeft-handedBowlingRight-arm leg breakRoleBowlerInternational information National sideAustraliaTest debut (cap 140)29 January 1932 v South AfricaLast Te...

Latin designation for the Berber population of Mauretania Not to be confused with Moriori, Māori people, or Maouri people.For other uses, see Mauri (disambiguation). Mauretanian cavalry under Lusius Quietus fighting in the Dacian Wars, from the Column of Trajan Mauri (from which derives the English term Moors) was the Latin designation for the Berber population of Mauretania, located in the west side of North Africa on the shores of the Mediterranean Sea, Mauretania Tingitana and Mauretania ...

1944 United States Senate election in North Dakota ← 1938 November 7, 1944 1946 (special) → Nominee John Moses Gerald Nye Lynn Stambaugh Party Democratic Republican Independent Republican Popular vote 95,102 69,530 44,596 Percentage 45.20% 33.04% 21.19% County resultsMoses: 30–40% 40–50% 50–60% 60–70% Nye: &#...

Scalabrini Ortiz UbicaciónCoordenadas 34°35′07″S 58°24′57″O / -34.58516667, -58.41597222Dirección Av. Santa Fe 3700Barrio PalermoComuna 14Ciudad Buenos AiresDatos de la estaciónNombre anterior Canning (1938 - 1974)2 de abril(Brevemente en 1982)Punto kilométrico 4,8 kmInauguración 29 de diciembre de 1938 (85 años)Servicios N.º de andenes 2 (lateral)N.º de vías 2Tipología SubterráneaPropietario Subterráneos de Buenos AiresOperador EmovaColectivos 12 15...

The City of Port St. Lucie, FloridaKotaPGA Golf Club, located in Port St. LucieJulukan: PSLMotto: A City for All AgesLocation in St. Lucie County and the state of FloridaU.S. Census MapNegara Amerika SerikatNegara bagian FloridaCounty St. LucieDibentukApril 27, 1961Pemerintahan • MayorJoAnn FaiellaLuas • Kota76,7 sq mi (198,6 km2) • Luas daratan75,5 sq mi (195,6 km2) • Luas perairan1,1 ...

Village and civil parish in Surrey, England Human settlement in EnglandCapelShiremark MillCapelLocation within SurreyArea26.14 km2 (10.09 sq mi)Population3,832 (Civil Parish 2011)[1]• Density147/km2 (380/sq mi)OS grid referenceTQ1740Civil parishCapelDistrictMole ValleyShire countySurreyRegionSouth EastCountryEnglandSovereign stateUnited KingdomPost townDorkingPostcode districtRH5Dialling code01306PoliceSurreyFireSurreyAmbul...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (نوفمبر 2019) فريدي ويكسلر معلومات شخصية الميلاد 19 مايو 1986 (38 سنة) مواطنة الولايات المتحدة الحياة العملية المهنة صاحب أعمال، ومغني، ومغن مؤلف، ومنتج �...

Cervignano del FriuliKomuneCittà di Cervignano del FriuliNegaraItaliaWilayahFriuli-Venezia GiuliaProvinsiUdine (UD)FrazioniScodovacca, Strassoldo, MuscoliPemerintahan • Wali kotaGianluigi SavinoLuas • Total28 km2 (11 sq mi)Ketinggian2 m (7 ft)Populasi (2011) • Total13.673 • Kepadatan490/km2 (1,300/sq mi)DemonimCervignanesiZona waktuUTC+1 (CET) • Musim panas (DST)UTC+2 (CEST)Kode pos33052Kode area t...

Irish technological university Technological University of the Shannon: Midlands MidwestOllscoil Teicneolaíochta na Sionainne: Lár Tíre Iarthar LáirLogo of the universityOther nameTUSTypePublic technological universityEstablished1 October 2021; 2 years ago (2021-10-01)ChairJosephine FeehilyPresidentVincent CunnaneTotal staff1,200+Students14,000+LocationIrelandColours Gold and blackWebsitetus.ie The Technological University of the Shannon: Midlands Midwest (TU...

1920 film Why Change Your Wife?Film posterDirected byCecil B. DeMilleWritten bySada CowanOlga PrintzlauStory byWilliam C. deMilleProduced byCecil B. DeMilleJesse L. LaskyStarringGloria SwansonCinematographyAlvin WyckoffEdited byAnne BauchensProductioncompanyFamous Players–Lasky/ArtcraftDistributed byParamount PicturesRelease date April 24, 1920 (1920-04-24)[1] Running time90 minutesCountryUnited StatesLanguagesSilentEnglish intertitlesBudget$129,349.31[2]Box o...

Atonismo AtónFundador(es) Akenatón y NefertitiFundación 1348 a. C.Deidad o deidades principales AtónTipo MonoteístaSeguidores conocidos como AtonistasPaís o región de origen Antiguo EgiptoLugares sagrados AmarnaSede AjetatónSímbolo Disco solarTemplos Pequeño templo de Atón Gran Templo de Atón[editar datos en Wikidata] El atonismo fue una de las primeras religiones monoteístas registradas en la historia.[1][2] Conocida también como religión de Atón,...

Longford-based Gaelic games club AbbeylaraMainistir LeathráthaFounded:1889County:LongfordColours:White and RedGrounds:Oliver Lynch Park, Ballyboy, AbbeylaraCoordinates:53°45′23″N 7°27′28″W / 53.756492°N 7.457706°W / 53.756492; -7.457706Playing kits Standard colours Senior Club Championships All Ireland Leinsterchampions Longfordchampions Football: - - 2 Abbeylara Gaelic Football Club is a Gaelic football club based in Abbeylara, County Longford, Irela...

Citation index of legal resources Shepardizing redirects here. Not to be confused with Sherardizing. Shepard's Citations is a citator used in United States legal research that provides a list of all the authorities citing a particular case, statute, or other legal authority.[1] The verb Shepardizing (sometimes written lower-case) refers to the process of consulting Shepard's to see if a case has been overturned, reaffirmed, questioned, or cited by later cases.[1] Prior to the ...

بطولة كاريوكا 1966 تفاصيل الموسم بطولة كاريوكا البلد البرازيل البطل نادي بانغو أتلتيكو بطولة كاريوكا 1965 بطولة كاريوكا 1967 تعديل مصدري - تعديل بطولة كاريوكا 1966 هو موسم من بطولة كاريوكا. فاز فيه نادي بانغو أتلتيكو.[1][2] نتائج الموسم مراجع ^ Futebolnacional.com...

2017 action-adventure video game This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: The Lego Ninjago Movie Video Game – news · newspapers · books · scholar · JSTOR (October 2017) (Learn how and when to remove this message) 2017 video gameThe Lego Ninjago Movie Video GameDeveloper(s)TT FusionPublisher(s)Warner B...

French officer, engineer, physicist and mathematician Étienne-Louis MalusPortrait by Louis-Léopold Boilly, 1810Born23 July 1775Paris, FranceDied24 February 1812 (1812-02-25) (aged 36)Paris, FranceNationalityFrenchKnown forMalus's lawPlane of polarizationPolarization of lightMalus-Dupin theoremAwardsRumford Medal (1810)Scientific careerFieldsPhysics Étienne-Louis Malus (/ˈɛt.i.ɛn ˈluː.i məˈluːs/; French: [e.tjɛn.lwi ma.lys]; 23 July 1775 – 23 February 1...

La gastronomie associe l'art de bien préparer les repas, de sélectionner des produits plus ou moins travaillés (fromages, par exemple) et celui de les déguster. La gastronomie est la connaissance raisonnée de tout ce qui se rapporte à l'être humain en tant qu'il se nourrit. Certains restreignent cela à l'ensemble des règles (fluctuantes, selon pays, classes sociales et modes) qui définissent l'art de faire bonne chère[1]. Selon l'Académie française, l'expression « faire bon...