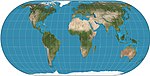
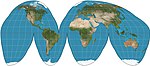
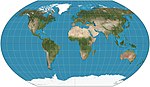
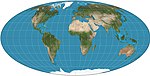
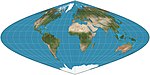
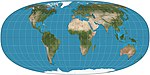
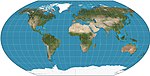
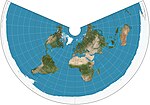
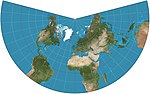
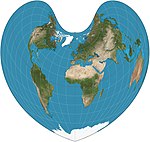
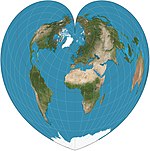
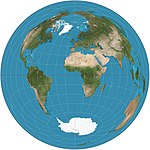
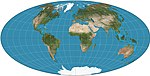
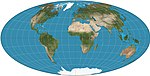
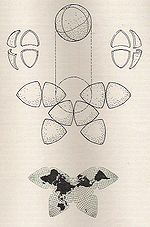
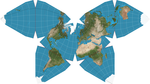
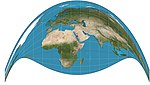
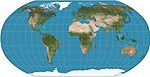
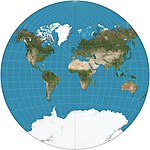
Список картографических проекций

В этом списке картографические проекции рассортированы по виду поверхности проектирования. Традиционно выделяют три категории проекций: цилиндрические, конические и азимутальные. Некоторые проекции трудно отнести к какой-либо из этих трёх категорий. С другой стороны, проекции можно классифицировать по характеристикам поверхности, которые они оставляют неизменными: направления, локальную форму, площадь и расстояние.

Таблица проекций

Цилиндрические

Основная статья: Цилиндрические картографические проекции

Термин «цилиндрическая проекция» используются по отношению к любой проекции, для которой меридианы проецируются в равноотстоящие вертикальные линии, а параллели — в горизонтальные линии.

Проекция Пример Создатель Год Примечания
Равнопромежуточная проекция Марин Тирский ок. 120 г. н. э. Простая геометрия; сохраняет расстояния вдоль экватора и всех меридианов
Галла — Петерса Джеймс Галл,

Арно Петерс

1855 Равновеликая
Равновеликая цилиндрическая проекция Ламберта Иоганн Ламберт 1772 Равновеликая
Проекция Меркатора Герард Меркатор 1569 Сохраняет углы,

не может отображать полюса

Цилиндрическая проекция Миллера Осборн Миллер[англ.] 1942 Отображает полюса
Центральная цилиндрическая проекция[англ.] XIX в. Используется в панорамной фотографии

Псевдоцилиндрические

Основная статья: Псевдоцилиндрические картографические проекции

Псевдоцилиндрические проекции представляют центральный меридиан и все параллели в виде отрезков прямых, проекции прочих меридианов не являются прямыми[1].

Проекция Пример Создатель Год Примечания
Проекция Эккерта IV Макс Эккерт-Грейфендорфф[англ.]
Проекция Эккерта VI Макс Эккерт-Грейфендорфф[англ.]
Проекция Гуда Джон Гуд[англ.] 1923
Проекция Каврайского В. В. Каврайский 1939
Моллвейде[англ.] Карл Моллвейде 1805
Синусоидальная проекция Николя Сансон

Флемстид, Джон

Гиперэллиптическая проекция Тоблера Валдо Тоблер[англ.] 1973
Проекция Вагнера К. Х. Вагнер[англ.]
Хельцель Хельцель Ок. 1960

Конические

Основная статья: Конические картографические проекции
Проекция Пример Создатель Примечания
Равнопромежуточная[англ.] Птолемей
Равноугольная Ламберта Иоганн Ламберт

Псевдоконические

Проекция Пример Создатель Примечания
Проекция Бонне Ригобер Бонне
Проекция Вернера Иоганнес Вернер[англ.],
Иоганнес Стабиус
Поликоническая[англ.] Фердинанд Хасслер[англ.]

Азимутальные

Основная статья: Азимутальные картографические проекции

Азимутальные проекции сохраняют направления из центральной точки (и следовательно, большие окружности, проходящие через центральную точку, представлены прямыми на карте). Как правило, такие проекции также имеют радиальную симметрию масштабов, а значит и искажений: расстояния на карте из центральной точки вычисляются по функции r(d) от истинного расстояния d, независимо от угла; соответственно, круги с центром в центральной точке представлены кругами с центром в центральной точке на карте.

Проекция Пример Создатель Примечания
Азимутальная проекция Эта проекция используется Геологической службой США в Национальном Атласе США, а также в эмблеме ООН.
Равновеликая азимутальная проекция Ламберта Иоганн Ламберт

Псевдоазимутальные

Проекция Пример Создатель Примечания
Аитова[англ.] Давид Аитов
Хаммера[англ.] Эрнст Хаммер[англ.]
Тройная Винкеля[англ.] Освальд Винкель[англ.]

Полиэдрические

Основная статья: Геодезические сетки

Полиэдрические проекции проецируют поверхность геоида на различные многогранные аппроксимации сферы. В качестве проекции на каждую грань часто используется гномоническая проекция, но некоторые картографы предпочитают равновеликую проекцию Фишера-Снайдера или равноугольную проекцию[2].

Проекция Пример Создатель Примечания
«Бабочка» Кахилла Бернард Кэххил
«Бабочка» Уотермана[англ.] Стив Уотерман[англ.]
Квадрилатеральный сферический куб[англ.] Ф. Кеннетт Чан, Э. М. О`Нил Равновеликая
Проекция Пирса[англ.] Чарлз Пирс Равноугольная
Проекция Димаксион Бакминстер Фуллер Уменьшение искажений ценой нарушения непрерывности карты
Мириаэдрическая проекция Джек Ван Вийк[англ.] Проекция глобуса на так называемый «мириаэдр» — многогранник с несколькими тысячами граней.[3][4]

Проекции по их метрическим свойствам

Равноугольные

Проекция Пример Создатель Примечания
Равноугольная коническая проекция Ламберта Иоганн Ламберт Не отображает южный полюс
Проекция Меркатора Герард Меркатор Не отображает полюса
Проекция Пирса[англ.] Чарльз Пирс Равноугольная

Равновеликие

Гибридные карты, использующие в одних регионах одну равновеликую проекции, а в других — другую:

  • HEALPix[англ.]: Равновеликие цилиндрические проекции Колиньона и Ламберта;
  • Гомолосинусоидальная проекция Гуда: синусоидальная + Мольвельде;
  • Philbrick Sinu-Mollweide: синусоидальная + Мольвельде, косая, ненепрерваная[5].
  • Асимметричная проекция Хатано: две разные псевдоцилиндрические проекции равной площади соединяются на Экваторе.

Многогранные равноплощадые карты обычно используют равновеликую проекция Ирвинга Фишера, в то время как большинство многогранных равноплощадых карт используют гномоническую прокцию.[6]

Равнопромежуточные

Равнопромежуточная проекция двух точек[англ.] Азии

Равнопромежуточные проекции сохраняют расстояние между некоторыми стандартными точками или линиями.

Гномоническая

Проекция Пример Создатель Примечания
Гномоническая

Ретроазимутальная

Проекция Пример Создатель Примечания
Ретроазимутальная проекция Крейга

Компромиссные проекции

Проекция Пример Создатель Примечания
Проекция Робинсона[англ.] Артур Робинсон Компромисс между конформными и равновеликими проекциями
Проекция Ван дер Гринтена Альфонс ван дер Гринтен Компромисс между конформными и равновеликими проекциями
Цилиндрическая проекция Миллера Osborn Maitland Miller[англ.]
Тройная проекция Винкеля[англ.] Винкель, Освальд[англ.] Эта проекция — среднее арифметическое между равнопромежуточной проекцией и проекцией Айтофа
Проекция Димаксион Бакминстер Фуллер Уменьшает искажения путём потери неразрывности поверхности
«Бабочка» Кахилла[англ.] Бернард Кахилл[англ.]
«Бабочка» Уотермана[англ.] Стив Уотерман[англ.]
Проекция Каврайского В. В. Каврайский
Проекция Вагнера Эквивалентна проекции Каврайского с коэффициентом горизонтального масштабирования .

Примечания

  1. ↑ Картографические проекции. Дата обращения: 19 декабря 2015. Архивировано 14 сентября 2016 года.
  2. ↑ Carlos A. Furuti. «Polyhedral Maps» Архивная копия от 15 августа 2008 на Wayback Machine.
  3. ↑ Jarke J. van Wijk Unfolding the Earth: Myriahedral Projections Архивная копия от 20 июня 2020 на Wayback Machine.
  4. ↑ Carlos A. Furuti. «Interrupted Maps: Myriahedral Maps». [1] Архивная копия от 17 января 2020 на Wayback Machine
  5. ↑ Geocart Projections. Дата обращения: 19 декабря 2015. Архивировано 26 октября 2015 года.
  6. ↑ «Polyhedral Maps» by Carlos A. Furuti. Дата обращения: 9 января 2012. Архивировано 15 августа 2008 года.
  7. ↑ arcgis.com Архивная копия от 4 марта 2016 на Wayback Machine Проекция Кассини — Зольднера
  8. ↑ Carlos A. Furuti. Conic Projections: Equidistant Conic Projections Архивная копия от 30 ноября 2012 на Wayback Machine
  9. ↑ Равнопромежуточная коническая проекция. Дата обращения: 26 декабря 2015. Архивировано 27 декабря 2015 года.
  10. ↑ Проекция равнопромежуточная двух точек
  11. ↑ arcgis.com Архивная копия от 27 декабря 2015 на Wayback MachineОртографическая проекция
  12. ↑ Азимутальная равновеликая проекция Ламберта. Дата обращения: 26 декабря 2015. Архивировано 27 декабря 2015 года.
  13. ↑ arcgis.com Архивная копия от 27 декабря 2015 на Wayback Machine Поликоническая проекция

Ссылки

Read other articles:

Kasus uji emisi Volkswagen

Kasus uji emisi Volkswagen2010 VW Golf TDI Clean DieselTanggal2009–2015LokasiSeluruh duniaJenisPelanggaran standar emisi dan kecurangan uji emisiPenyebabMengurangi emisi hanya ketika menjalani uji emisiPeserta/Pihak terlibatPelaku: Volkswagen GroupRegulator: Badan Perlindungan Lingkungan Amerika Serikat (US EPA), regulator lainnya. Timeline1999US EPA mengumumkan perubahan regulasi, batas NOx dikurangi dari 1.0 g/mi to .07 g/mi2004-2009Regulasi emisi disel mulai dijalankan2007VW menghentikan...

 

 

Dorkas

Penyembuhan Dorkas oleh Masolino da Panicale, 1425. Dorkas (nama Yunani), dalam Bahasa Aram disebut Tabita,[1] adalah salah satu tokoh perempuan dalam Alkitab, khususnya pada bagian Perjanjian Baru di Alkitab Kristen, di dalam kitab Kisah Para Rasul.[2] Selain itu, Dorkas juga dikenal sebagai santa.[3] Ia banyak melakukan pelayanan kasih selama hidupnya.[2] Ia membuat pakaian bagi orang-orang miskin, berbuat baik, dan memberi sedekah.[4] Kematian dan ke...

 

 

Caenorhabditis elegans

Free-living species of nematode C. elegans redirects here. For other uses, see C. elegans (disambiguation). Caenorhabditis elegans An adult hermaphrodite C. elegans worm Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Nematoda Class: Chromadorea Order: Rhabditida Family: Rhabditidae Genus: Caenorhabditis Species: C. elegans Binomial name Caenorhabditis elegans(Maupas, 1900)[1] Subspecies Caenorhabditis elegans var. Bergerac[2] (for instance strain BO...

Zafar Mahal (Mehrauli)

Building in Delhi, IndiaZafar MahalZafar Gate of Zafar MahalLocation within IndiaGeneral informationArchitectural styleMughal ArchitectureTown or cityDelhiCountryIndiaCoordinates28°30′57″N 77°10′39″E / 28.5158°N 77.1775°E / 28.5158; 77.1775Completed19th centuryDemolishedRuinsClientMughal dynastyDesign and constructionArchitect(s)Akbar Shah II and Bahadur Shah Zafar II Zafar Mahal, in Mehrauli village, in South Delhi, India, is considered as the last monume...

 

 

Solar power in Georgia (U.S. state)

Overview of solar power in the U.S. state of Georgia Solar roof, Murray Elementary School, Fort Stewart Solar power in Georgia on rooftops can provide 31% of all electricity used in Georgia.[1] Net metering is limited to 100 kW for non-residential consumers and 10 kW for residential consumers, up to 0.2% of previous years peak demand. Georgia was given an F for net metering.[2][3] Georgia is not a Net Metering State.[4] Old Midville solar project, Mil...

 

 

哈萨克斯坦总统

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言，清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日（哈薩克蘇維埃社會主義共和國總統） 哈萨克斯坦 哈萨克斯坦政府...

Sekolah menengah agama Katolik

Bagian dari seriPendidikan di Indonesia Kementerian Pendidikan, Kebudayaan, Riset, dan Teknologi Republik Indonesia Pendidikan anak usia dini TK RA KB Pendidikan dasar (kelas 1–6) SD MI Paket A Pendidikan dasar (kelas 7–9) SMP MTs Paket B Pendidikan menengah (kelas 10–12) SMA MA SMK MAK SMA SMTK SMAK Utama Widya Pasraman Paket C Pendidikan tinggi Perguruan tinggi Akademi Akademi komunitas Institut Politeknik Sekolah tinggi Universitas Lain-lain Madrasah Pesantren Sekolah alam Sekolah ru...

 

 

Pengalih KVM

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2016. Diagram cara kerja Pengalih KVM. Pengalih KVM (singkatan dari Keyboard, Video, Mouse switch) adalah sebuah alat elektronik yang mengizinkan satu buah papan ketik, tetikus (atau perangkat penunjuk lainnya), dan video untuk mengontrol sejumlah komputer s...

 

 

Oden

Untuk kegunaan lain, lihat Oden (disambiguasi).Oden Oden (おでん atau 御田code: ja is deprecated ) adalah salah satu masakan Jepang jenis nabemono (rebusan panas dalam panci ala Jepang). Oden merupakan campuran beberapa bahan yang direbus di dalam kuah dari dashi dan kecap asin. Bahan-bahan dimasukkan dalam oden adalah lobak, konnyaku, telur rebus, chikuwa, chikuwabu, dan lain sebagainya. Oden merupakan makanan yang umum dimakan di musim dingin dan langsung dimakan selagi masih panas-pan...

Palghar Lok Sabha constituency

Lok Sabha constituency in Maharashtra Palghar Lok SabhaLok Sabha constituencyDark Area of ConstituencyConstituency detailsCountryIndiaRegionWestern IndiaStateMaharashtraAssembly constituenciesDahanuVikramgadPalgharBoisarNalasoparaVasaiEstablished2008Total electors17,31,077[1]ReservationSTMember of Parliament17th Lok SabhaIncumbent Rajendra Gavit PartyShiv SenaElected year2019Preceded byChintaman Vanaga, BJP Palghar Lok Sabha constituency is one of the 48 Lok Sabha (lower house of Indi...

 

 

Zigaz (album)

ZigazAlbum studio karya ZigazDirilis1 Mei 2009GenreRockLabelBNG EntertainmentKronologi Zigaz Zigaz (2009) Kenanglah (2015)Kenanglah2015 ZIGAZ merupakan sebuah album musik pertama karya Zigaz . Dirilis pada tahun 2009 dengan lagu utamanya yang berjudul Sahabat Jadi Cinta, Hidupmu Hidupku, T.A.R. (Teman Atau Ratu), Hanya Untuk Hari Ini. Daftar lagu Aku Adalah Aku Sahabat Jadi Cinta Penakluk Takluk Harmoni Apakah Dosa T.A.R. (Teman Atau Ratu) Hanya Untuk Hari Ini Hidupmu Hidupku Sesungguhnya...

 

 

Fireboats of San Diego

San Diego's first fireboat, the Bill Kettner.[1] Fireboats in San Diego have been operated on San Diego Bay by the city of San Diego, California since the early 20th century, as well as by the Port of San Diego since its creation as a quasi-governmental agency serving the entire Bay in 1962. City of San Diego Fire-Rescue Department The city's first fireboat, the Bill Kettner, was named after San Diego's Congressional Representative William Kettner. [2] The vessel was built by ...

Mercado Pino Suárez

Market in Mazatlán Pino Suárez MarketMercado Pino SuárezPino Suárez Market in 2022Former namesMercado Manuel Romero Rubio (May 5, 1899-February 13, 1915)Alternative namesMercado Municipal José María Pino SuárezGeneral informationTypeCovered marketLocationMazatlán, MexicoCoordinates23°12′08″N 106°25′16″W / 23.202211°N 106.421146°W / 23.202211; -106.421146Named forJosé María Pino SuárezYear(s) built1895-1899Construction started1895Completed1899Open...

 

 

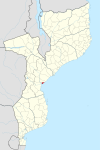
Beira, Mozambik

Beira, Mozambik kotamunicipality of Mozambique (en) kota besar Beira (pt) Tempat RepublikMozambiqueProvinsi di MozambikProvinsi SofalaDistrict of Mozambique (en) Beira District (en) Ibu kota dariProvinsi Sofala Beira District (en) NegaraMozambique PendudukTotal530.604  (2019 )GeografiLuas wilayah633 km² [convert: unit tak dikenal]Ketinggian14 m SejarahPembuatan1887 Informasi tambahanKode pos2100 Zona waktuUTC+1 Lain-lainKota kembarBenderBristolPadovaSeixal (en) AmsterdamCoimbraEspi...

 

 

Pier Angelo Boffi

Questa voce sull'argomento calciatori svizzeri è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Pier Angelo BoffiNazionalità Svizzera Calcio RuoloDifensore CarrieraGiovanili  Rapid Lugano Squadre di club1 1964-1965 Lugano? (?)1965-1966 Blue Stars Zurigo? (?)1966-1969 Chiasso? (?)1969-1972 Lugano? (?)1972-1974 Young Boys? (?)1974-? Chiasso? (?) Nazionale 1970-1973...

هاري ليدر

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (مارس 2019) هاري ليدر معلومات شخصية تاريخ الميلاد 10 مارس 1880 [1]  تاريخ الوفاة 9 مايو 1946 (66 سنة) [1]  مواطنة كندا  الحياة العملية المهنة سياسي،  وفلاح  الحز...

 

 

Русская эскадра

Русская эскадра Годы существования 21 ноября 1920 — 30 октября 1924 Входит в Русская армия Тип военно-морской флот Дислокация Бизерта, в то время - заморский регион Франции Прозвище врангелевцы Цвета бело-сине-красный Участие в Гражданская война в России Командиры Известные к...

 

 

Stephen Gardiner

Untuk arsitek Inggris, lihat Stephen Gardiner (arsitek). Untuk atlet Bahama, lihat Steven Gardiner. The Right ReverendStephen GardinerUskup WinchesterGerejaGereja Katolik / Gereja InggrisProvinsi gerejawiCanterburyKeuskupanWinchesterMasa jabatan1531–1551, 1553–1555Jabatan lainLord ChancellorMaster of Trinity Hall, CambridgeImamatTahbisan uskup3 Desember 1531Informasi pribadiLahirca 1483Bury St EdmundsWafat12 November 1555MakamKatedral Winchester51°03′38″N 1°18′47″W...

Attitude change

Theory of change of associated beliefs and behaviours Attitudes are associated beliefs and behaviors towards some object.[1][2] They are not stable, and because of the communication and behavior of other people, are subject to change by social influences, as well as by the individual's motivation to maintain cognitive consistency when cognitive dissonance occurs—when two attitudes or attitude and behavior conflict. Attitudes and attitude objects are functions of affective an...

 

 

MVP 06: NCAA Baseball

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: MVP 06: NCAA Baseball – news · newspapers · books · scholar · JSTOR (July 2014) (Learn how and when to remove this message) 2006 video gameMVP 06: NCAA BaseballNorth American cover art for PlayStation 2Pictured: David MaroulDeveloper(s)EA CanadaPublisher(s)Elec...