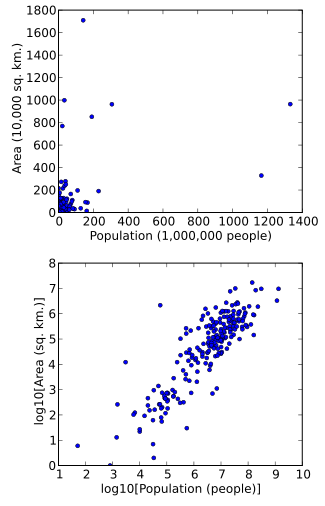
Преобразование данных (статистика)
|
Read other articles:

2006 French filmLe Grand MeaulnesFilm posterDirected byJean-Daniel VerhaegheWritten byAlain-Fournier (novel)Jean CosmosJean-Daniel Verhaeghe (screenplay)Produced byPascal HouzelotStarringNicolas DuvauchelleJean-Baptiste MaunierClémence PoésyJean-Pierre MariellePhilippe TorretonCinematographyYves LafayeEdited byDominique FaysseMusic byPhilippe SardeProductioncompanyMosca FilmDistributed byTFM DistributionRelease date 4 October 2006 (2006-10-04)[1] Running time97 minute...

Ju 52 JU Air Junkers Ju 52/3m HB/HOS in flight over Austria (July 2013) Jenis Pesawat terbang Pembuat Junkers Perancang Ernst Zindel Penerbangan perdana 13 Oktober 1930 (Ju 52/1m); 7 Maret 1932 (Ju 52/3m) Status Dalam penggunaan terbatas Pengguna utama LuftwaffeLuft HansaAngkatan Udara Spanyol Dibuat 1931–1945 (Jerman)1945–1947 (Prancis)1945–1952 (Spanyol) Jumlah 4,845 Junkers Ju 52 adalah pesawat angkut yang dirancang dan diproduksi oleh perusahaan penerbangan Jerman, Junkers. Pe...

Chemical compound PramocaineClinical dataTrade namesAnalpram HC, Caladryl, Caladryl Clear, Cortane-B, Epifoam, Gold Bond Maximum Relief, Itch-X, Pramosone, Prax, Proctodan-HC, Proctofoam, Tronolane, Vagisil MedicatedAHFS/Drugs.comInternational Drug NamesMedlinePlusa682429License data US DailyMed: 8bfeea34-25d5-4721-a17f-d9f1d0084cc3, 81ab7fa7-d9b0-49dc-9782-02f37e588c5e Routes ofadministrationTopical, rectal, VaginalATC codeD04AB07 (WHO) C05AD07 (WHO)Legal statusLegal...

Apple Arcade Informations Développé par Apple Première version 19 septembre 2019 Système d'exploitation iOS, iPadOS, tvOS, macOS Environnement Apple TV, macOS, iOS, iPadOS et tvOS Type AbonnementÉditeur de jeux vidéo Site web https://www.apple.com/fr/apple-arcade/ modifier - modifier le code - voir Wikidata (aide) Apple Arcade est un service d'abonnement aux jeux vidéo proposé par Apple. Il a été lancé le 19 septembre 2019 lors de la présentation annuelle principale d'Apple...

H.Saan MustopaM.Si. Anggota Dewan Perwakilan RakyatRepublik IndonesiaPetahanaMulai menjabat 1 Oktober 2019Daerah pemilihanJawa Barat VII Informasi pribadiLahir5 Juli 1968 (umur 55)Karawang, Jawa Barat, IndonesiaKebangsaanIndonesiaPartai politikPartai Demokrat (2007–2016)Partai Nasional Demokrat (2016–sekarang)Suami/istriIlah HolilahAlma materUniversitas IndonesiaPekerjaanPolitikusSunting kotak info • L • B Saan Mustopa (lahir 5 Juli 1968[1]) atau kerap dipan...

Pour les articles homonymes, voir Jean-Jean. Cet article est une ébauche concernant un animateur de radio français. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les pratiques du projet Radio. Éric Jean-JeanÉric Jean-Jean le 14 juillet 2011, au concert pour l'égalité de SOS Racisme.FonctionsAnimateur audiovisuelBiographieNaissance 20 septembre 1967 (56 ans)Blaye (Gironde, France)Nationalité FrançaiseFormation Institut d'études politiques de Bo...

Европейская сардина Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеГруппа:Костные рыбыКласс:Лучепёрые рыбыПодкласс:Новопёры...

Breast ornament worn in Ancient Egypt Senusret II's pectoral, by 1878 BC. Hieroglyphs: Ankh, Huh (god)-(=millions), Shen ring, scarab, Ra, Water Ripple, Sun-rising hieroglyph, uraeus The pectorals of ancient Egypt were a form of jewelry, often in the form of a brooch. They are often also amulets, and may be so described. They were mostly worn by richer people and the pharaoh. One type is attached with a nah necklace, suspended from the neck and lying on the breast. Statuary from the Old Kingd...

US college athletic conference Ohio Valley ConferenceAssociationNCAAFounded1948CommissionerBeth DeBauche (since 2009)Sports fielded 20 men's: 9 women's: 10 coeducational: 1 DivisionDivision ISubdivisionFCSNo. of teams11HeadquartersBrentwood, TennesseeRegionMidwest and SouthOfficial websitewww.ovcsports.comLocations UA Little RockEastern IllinoisLindenwoodMorehead StateSEMOSIUEUSITenn StateTenn TechUT MartinWestern Illinoisclass=notpageimage| Ohio Valley Conference The Ohio Valley Conference (...

Pour les articles homonymes, voir Chéret. Jules ChéretJules Chéret photographié par Nadar vers 1900.BiographieNaissance 31 mai 1836Ancien 11e arrondissement de ParisDécès 23 septembre 1932 (à 96 ans)NiceSépulture Cimetière Saint-VincentNom de naissance Jean Jules ChéretNationalité françaiseActivités Lithographe (à partir du 1er juillet 1866), artiste graphique, créateur de bijoux, designer, affichiste, lithographe, peintreFratrie Joseph ChéretAutres informationsMouvement...

Subgenre of Chinese fantasy fiction A late Ming printed edition of The Three Sui Quash the Demons' RevoltTraditional Chinese神魔小說Simplified Chinese神魔小说TranscriptionsStandard MandarinHanyu Pinyinshénmó xiǎoshuōIPA[ʂə̌nmwǒ ɕjàʊʂwó] Gods and demons fiction or Shenmo fiction (traditional Chinese: 神魔小說; simplified Chinese: 神魔小说; pinyin: shénmó xiǎoshuō) is a subgenre of Chinese fantasy fiction that revolves ar...

Cet article est une ébauche concernant la Grèce et l’histoire. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Province de l'Epire en orange La révolte épirote de 1854 est un soulèvement nationaliste grec qui éclate en Épire, alors une province ottomane, le pachalik de Ioannina, au moment de la Guerre de Crimée (1853-1856). Cette révolte reçoit un important soutien de l'opinion publique du royaume de...

British-bred Thoroughbred racehorse Night HawkNight Hawk in 1913.SireGallinuleGrandsireIsonomyDamJean's FollyDamsireAyrshireSexStallionFoaled1910[1]CountryUnited Kingdom of Great Britain and IrelandColourBayBreederWilliam Hall WalkerOwnerWilliam Hall WalkerTrainerWilliam Jack RobinsonRecord10: 1-2-1Earnings£6,450[2]Major winsSt Leger (1913) Night Hawk (1910 – after 1924) was an Irish-bred, British-trained Thoroughbred racehorse and sire. He was unraced as a juvenile and...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Oktober 2022. Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya ...

This article details all-time records. For a season-by-season statistical breakdown see List of York City F.C. seasons. Norman Wilkinson, York City's top goalscorer with 143 goals in all competitions York City Football Club is a professional association football club based in York, North Yorkshire, England. The club was founded in 1922 and was elected to the Midland League, which the team played in until 1929 when they were elected to the Football League. The highest level of the English foo...

Eastern Catholic church Not to be confused with the Syro-Malabar Church, another Eastern Catholic body. Syro-Malankara Catholic ChurchOld image of Cathedral of Saint Mary, Pattom, TrivandrumTypeParticular church (sui iuris)ClassificationEastern CatholicOrientationEastern ChristianityScripturePeshitta[1]TheologyCatholic theologyPolityEpiscopal polityPopeFrancisMajor ArchbishopBaselios CleemisParishes1096[citation needed]LiturgyWest Syriac Rite (Malankara Rite)HeadquartersCathed...

У этого термина существуют и другие значения, см. Свод (значения). Готические своды Сен-Шапель Свод (от «сводить» — соединять, смыкать) — в архитектуре тип перекрытия или покрытия пространства (помещения), ограниченного стенами, балками или столбами — конструкция, к�...

U.S. House district for Indiana Indiana's 6th congressional districtIndiana's 6th congressional district since January 3, 2023RepresentativeGreg PenceR–ColumbusArea5,550.4 sq mi (14,375 km2)Distribution59.23% urban40.77% ruralPopulation (2022)758,725Median householdincome$69,426[1]Ethnicity81.0% White5.3% Hispanic5.3% Asian4.0% Black3.9% Two or more races0.6% otherCook PVIR+19[2] Indiana's 6th congressional district is a congressional district in the U.S. stat...

First Dibbs ministry21st Cabinet of the Colony of New South Wales Premier George Dibbs and the Colony of New South Wales (1863–1900)Date formed7 October 1885 (1885-10-07)Date dissolved21 December 1885 (1885-12-21)People and organisationsMonarchQueen VictoriaGovernorLord Augustus Loftus / The Lord CarringtonHead of governmentGeorge DibbsNo. of ministers10Member partyunalignedStatus in legislatureMinority governmentOpposition partyunalignedOpposition leaderJohn ...

この項目では、香港を発端に起こった世界的株価大暴落について説明しています。ブラックフライデーの次の段階については「ウォール街大暴落 (1929年)」をご覧ください。 この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典がまったく示されていないか不十分です。内容に関する文献や情報源が必要です。(2021年3月) 独自研�...