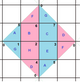
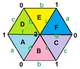
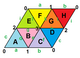
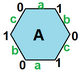
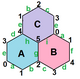
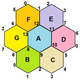
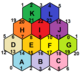
Правильная карта (теория графов)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

AuditionPoster rilis teatrikalSutradaraTakashi MiikeProduserSatoshi FukushimaAkemi SuyamaToyoyuki YokohamaSkenarioDaisuke TenganBerdasarkanAudition karya Ryu MurakamiPemeranRyo IshibashiEihi ShiinaPenata musikKōji EndōSinematograferHideo YamamotoPenyuntingYasushi ShimamuraPerusahaanproduksiAFDFCreators Company ConnectionOmega Project Inc.DistributorVitagraph Films (AS)Tanggal rilis2 Oktober 1999 (Festival Film Internasional Vancouver) 3 Maret 2000 (Jepang)Durasi115 menitNegaraJepangBa...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Kerajaan Sontang – berita · surat kabar · buku · cendekiawan · JSTOR Kerajaan Sontang adalah salah satu kerajaan di Provinsi Sumatera Barat. Kerajaan Sontang bergabung dalam Republik Indonesia pada tahun...

Ini adalah nama Korea; marganya adalah Park. Park Woo-jinNama asal박우진Lahir2 November 1999 (umur 24)Distrik Saha, Busan, Korea SelatanKebangsaanKorea SelatanPekerjaanPenyanyipenyanyi rapTahun aktif2017 (2017)–sekarangAgenBrand New MusicKarier musikGenreK-popInstrumenVokalLabelYMC Entertainment (2017–2018)Brand New Music (2018-sekarang)Artis terkaitWanna One, AB6IXTanda tangan Nama KoreaHangul박우진 Hanja朴佑鎮[1] Alih AksaraPark Woo-jinMcCune–Reisc...

Konsulat Jenderal Republik Indonesia di MelbourneConsulate General of the Republic of Indonesia in Melbourne Koordinat37°51′06″S 144°58′45″E / 37.851691°S 144.979297°E / -37.851691; 144.979297Lokasi Melbourne, AustraliaAlamat72 Queens RoadMelbourne, Victoria, AustraliaYurisdiksiVictoria dan TasmaniaKonsul JenderalKuncoro Giri WasesoSitus webkemlu.go.id/melbourne/id Konsulat Jenderal Republik Indonesia di Melbourne (KJRI Melbourne) (Inggris: Consulate Ge...

Egidio Capra Nazionalità Italia Altezza 165 cm Peso 65 kg Calcio Ruolo Allenatore (ex ala) Termine carriera 1949 - giocatore Carriera Giovanili 1928-1931 Adda di Lodi (ULIC) Squadre di club1 1931-1936 Fanfulla? (39)1936-1939 Milano83 (20)1939-1941 Lucchese63 (14)1941-1942 Modena20 (2)1942-1943 Fanfulla31 (12)1944-1945 Pavia20 (7)1945-1946 Cremonese28 (6)1946-1947 Como41 (14)1947-1948 Legnano21 (6)1948-1949 Fanfulla? (?)1949-1953 S...

Public housing estate in Ma On Shan, Hong Kong Fu Fai GardenFu Fai GardenGeneral informationLocation28 On Shing Street, Ma On ShanNew Territories, Hong KongCoordinates22°25′29″N 114°14′00″E / 22.4248429°N 114.2334399°E / 22.4248429; 114.2334399StatusCompletedCategoryHome Ownership SchemeNo. of blocks2[1]No. of units520[1]ConstructionConstructed1991; 33 years ago (1991)ContractorsChina Civil Engineering Construction Corporat...

Roman goddess of liberty This article is about the Roman goddess. For other uses, see Libertas (disambiguation). LibertasGoddess of libertyLibertas with her attributes, on an aureus of TrajanSymbolPileus, rod (vindicta or festuca)EquivalentsGreek equivalentEleutheria Denarius (42 BC) issued by Cassius Longinus and Lentulus Spinther, depicting the crowned head of Libertas, with a sacrificial jug and lituus on the reverse Libertas (Latin for 'liberty' or 'freedom', pronounced [liːˈbɛrt̪...

Mountain range in Croatia This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Gorski Kotar – news · newspapers · books · scholar · JSTOR (March 2015) (Learn how and when to remove this message) Map of Gorski Kotar within Croatia. Gorski Kotar (Croatian: Gorski kotar, pronounced [ɡǒrski kôtaːr]; Engli...

Chronologies Chronologie Disney 1953 1954 1955 1956 1957 1958 1959Décennies :1920 1930 1940 1950 1960 1970 1980 Actualités de l'année Chronologie dans le monde 1953 1954 1955 1956 1957 1958 1959Décennies :1920 1930 1940 1950 1960 1970 1980Siècles :XVIIIe XIXe XXe XXIe XXIIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana,...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Mei 2016. SCI (Slavia Canal Internasional)Diluncurkan14 Desember 1994PemilikIvanenko V. V.SloganUntuk Slavia tentang Slavia dan dunia tentang orang Slav!Kantor pusat KievSitus webslav.tv SCI atau Slavia Canal Internasional didirikan di Ukraina tahun 1994. Pranala lu...

Place in the United StatesDuffy's CutEnclosure where the majority of human remains are believed to rest, possibly after having been moved[1]Coordinates: 40°02′14″N 75°31′57″W / 40.03722°N 75.53250°W / 40.03722; -75.53250 (accident site)CountryUnited StatesTownMalvern, Pennsylvania Duffy's Cut is the name given to a stretch of railroad tracks about 30 miles (48 km) west of Philadelphia, Pennsylvania, originally built for the Philadelphi...

Cengiz Ünder Ünder bersama timnas Turki pada 2018Informasi pribadiNama lengkap Cengiz Ünder[1]Tanggal lahir 14 Juli 1997 (umur 26)Tempat lahir Sındırgı, TurkiTinggi 1,73 m (5 ft 8 in)[2]Posisi bermain SayapInformasi klubKlub saat ini FenerbahçeNomor 20Karier junior2007–2013 Bucaspor2013–2015 AltınorduKarier senior*Tahun Tim Tampil (Gol)2014–2016 Altınordu 51 (11)2016–2017 İstanbul Başakşehir 32 (7)2017–2022 Roma 70 (13)2020–2021 →...

国民阵线Barisan NasionalNational Frontباريسن ناسيونلபாரிசான் நேசனல்国民阵线标志简称国阵,BN主席阿末扎希总秘书赞比里署理主席莫哈末哈山总财政希山慕丁副主席魏家祥维纳斯瓦兰佐瑟古律创始人阿都拉萨成立1973年1月1日 (1973-01-01)[1]设立1974年7月1日 (1974-07-01)前身 联盟总部 马来西亚 吉隆坡 50480 秋傑区敦依斯迈路太子世贸中心(英�...

Bilateral relationsGermany–Tanzania relations Germany Tanzania Germany–Tanzania relations are the bilateral relations between Germany and Tanzania. From 1885 to 1918, Tanzania (excluding Zanzibar) was a German colony as part of German East Africa. In the 21st century, relations are primarily characterized by the joint development cooperation. History In 1848, German missionaries Johannes Rebmann and Johann Ludwig Krapf were the first Europeans to discover Mount Kilimanjaro on behalf of th...

「アプリケーション」はこの項目へ転送されています。英語の意味については「wikt:応用」、「wikt:application」をご覧ください。 この記事には複数の問題があります。改善やノートページでの議論にご協力ください。 出典がまったく示されていないか不十分です。内容に関する文献や情報源が必要です。(2018年4月) 古い情報を更新する必要があります。(2021年3月)出...

Battle of Sugar PointPart of the American Indian WarsOjibways in a canoe on Leech Lake, 1896.DateOctober 5, 1898LocationLeech Lake, MinnesotaResult Chippewa victoryBelligerents Chippewa United StatesCommanders and leaders Bugonaygeshig John M. Bacon Melville Wilkinson †Strength 19 warriors 500Casualties and losses none killed 7 killed (including 1 Indian Policeman shot by mistake)19 wounded vteEnd of American Indian Wars(1895–1924) Renegade period Bannock Uprising Yaqui Upr...

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Siraja Oloan – berita · surat kabar · buku · cendekiawan · JSTOR Artikel atau bagian mungkin perlu ditulis ulang agar sesuai dengan standar kualitas Wikipedia. Anda dapat membantu memperbaikinya. Halaman pemb...

Elezioni regionali in Basilicata del 2024Stato Italia Regione Basilicata Data21-22 aprile Affluenza49,81% ( 3,71%) Candidati Vito Bardi Piero Marrese Partiti Forza Italia Partito Democratico Coalizioni Centro-destra – Az–IV Centro-sinistra – M5S Voti 153 00856,63% 113 97942,16% Seggi 13 / 21 8 / 21 Differenza % 14,43% 15,64[A 1]% Differenza seggi 0 0[A 2] Distribuzione del voto al presidente per comune Distribuzione del voto di lista per comune ...

England and Ireland international rugby league footballer Ben HarrisonPersonal informationFull nameBenjamin Jack Harrison[1]Born (1988-02-24) 24 February 1988 (age 36)[2]Barrow-in-Furness, Cumbria, EnglandHeight6 ft 1 in (1.85 m)Weight16 st 3 lb (103 kg) [3]Playing informationPositionLoose forward, Prop, Second-row Club Years Team Pld T G FG P 2006–16 Warrington Wolves 211 19 0 0 76 2007(loan) → Widnes Vikings 3 0 0 0...

Soumya SethSoumya Seth di peluncuran Yeh Hai AashiquiLahir17 Oktober 1989 (umur 34)Varanasi, Uttar Pradesh, IndiaKebangsaanIndonesiaPekerjaanAktrisTahun aktif2007–2016Suami/istriArun Kapoor (m. 2017; c. 2019)Anak1Kerabat Krushna Abhishek (sepupu) Arti Singh (sepupu) Ragini Khanna (sepupu) Govinda (paman) Keluargalihat keluarga Govinda Soumya Seth (Dewanagari: सोम्या सेठ; lahir 17 Oktober 1989) adalah seorang ak...