Полная линейная группа
|
Read other articles:

Seorang pengrajin yang tengah menyelesaikan pembuatan payung geulis.Lambang Kota Tasikmalaya Payung geulis (aksara Sunda: ᮕᮚᮥᮀ ᮌᮩᮜᮤᮞ᮪ pengucapan bahasa Sunda: [pajʊŋ gɤlis], EBSYD: payung gölis) adalah salah satu kerajinan berupa payung kertas yang berasal dari Kota Tasikmalaya. Payung ini terbuat dari anyaman bambu dengan penutup berbahan kertas yang dihias dengan motif atau corak khas berwarna-warni. Secara etimologis, payung geulis berasal dari bahasa Sunda yan...

Historic house in Virginia, United States United States historic placeWilomaU.S. National Register of Historic PlacesVirginia Landmarks Register Property entrance from U.S. Route 220Show map of VirginiaShow map of the United StatesLocationOff US 220, near Fincastle, VirginiaCoordinates37°30′53″N 79°53′20″W / 37.51472°N 79.88889°W / 37.51472; -79.88889Area40 acres (16 ha)Built1848 (1848), 1888Architectural styleGreek RevivalNRHP reference...
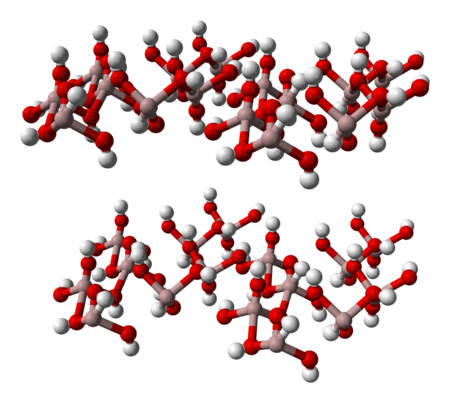
Hydroxyde d'aluminium Identification Nom UICPA hydroxyde d'aluminium Synonymes hydrate d'alumine trihydrate d'oxyde d'aluminium No CAS 21645-51-2 No ECHA 100.040.433 No CE 244-492-7 Apparence poudre blancheamorphe Propriétés chimiques Formule H3AlO3Al(OH)3 Masse molaire[1] 78,003 6 ± 0,001 1 g/mol H 3,88 %, Al 34,59 %, O 61,53 %, Propriétés physiques T° fusion 300 °C[2] Solubilité dans l'eau : nulle[2] M...

Commonwealth des Bahamas(en) Commonwealth of The Bahamas Drapeau des Bahamas Armoiries des Bahamas Devise en anglais : Forward, Upward, Onward Together (« Maintenir, croire et progresser ensemble ») Hymne en anglais : March On, Bahamaland (« En avant, Bahamas ») Fête nationale 10 juillet · Événement commémoré Indépendance vis-à-vis du Royaume-Uni (1973) Administration Forme de l'État Monarchie constitutionnelle Roi Charles I...

Law school in New Haven, Connecticut, US Yale Law SchoolCoat of arms of the law schoolParent schoolYale UniversityEstablished1824; 200 years ago (1824)School typePrivate law schoolEndowment$1.2 billionParent endowment$42.3 billion[1]DeanHeather K. GerkenLocationNew Haven, Connecticut, United States41°18′43″N 72°55′41″W / 41.312°N 72.928°W / 41.312; -72.928USNWR ranking1st (tie) (2024)[2]Bar pass rate99%[2]Websitelaw...

Fête de la Musique Fête de la Musique adalah perayaan musik tahunan yang berlangsung pada tanggal 21 Juni. Pada Hari Musik, warga dan penduduk dihimbau untuk memainkan musik di luar di lingkungan mereka atau di ruang publik dan taman. Konser gratis juga diselenggarakan, di mana musisi bermain untuk bersenang-senang dan bukan untuk dibayar.[1] Perayaan musik sepanjang hari pertama pada hari titik balik matahari musim panas berasal dari Jack Lang, Menteri Kebudayaan Prancis saat itu, ...

Aire d'attraction de Cluses Localisation de l'aire d'attraction de Cluses dans le département de la Haute-Savoie. Géographie Pays France Région Auvergne-Rhône-Alpes Département Haute-Savoie Caractéristiques Type Aire d'attraction d'une ville Code Insee 163 Catégorie Aires de 50 000 à moins de 200 000 habitants Nombre de communes 12 Population 56 061 hab. (2021) modifier L'aire d'attraction de Cluses est un zonage d'étude défini par l'Insee pour caract...

Turgut Özal Presiden Republik Turki ke-8Masa jabatan9 November 1989 – 17 April 1993PendahuluKenan EvrenPenggantiSüleyman Demirel Informasi pribadiLahir13 Oktober 1927MalatyaMeninggal17 April 1993AnkaraKebangsaanTurkiSuami/istriSemra ÖzalSunting kotak info • L • B Turgut Özal (13 Oktober 1927 – 17 April 1993) adalah pimpinan politik, perdana menteri, dan presiden Turki ke-8. Ia adalah tokoh politik dari Kurdi [1] Diarsipkan 2006-05-13 di Wayback Mac...

1962 Indian filmEk Musafir Ek HasinaaDVD coverDirected byRaj KhoslaWritten byRaj KhoslaProduced bySashadhar MukherjeeStarringJoy MukherjeeSadhanaCinematographyFali MistryEdited byS. E. ChandiwaleMusic byO. P. NayyarRaja Mehdi Ali Khan (lyrics)Release date1962CountryIndiaLanguageHindiBox office₹2,50,00,000[1] Ek Musafir Ek Hasina (English: A Traveller and A Beauty) is a 1962 Bollywood film directed by Raj Khosla and starring Joy Mukherjee, Sadhana in lead roles. The film was p...

Natalie ColeNatalie Cole nel 2007 Nazionalità Stati Uniti GenereJazzSwingPopRhythm and blues Periodo di attività musicale1975 – 2015 EtichettaCapitol, Excelsior Album pubblicati27 Sito ufficiale Modifica dati su Wikidata · Manuale Natalie Maria Cole (Los Angeles, 6 febbraio 1950 – Los Angeles, 31 dicembre 2015) è stata una cantante statunitense, figlia del cantante Nat King Cole[1]. Tra i maggiori successi della cantante: This Will Be e Sophisticat...

American political philosopher (1938–2002) Robert NozickNozick in 1977Born(1938-11-16)November 16, 1938New York City, U.S.DiedJanuary 23, 2002(2002-01-23) (aged 63)Cambridge, Massachusetts, U.S.EducationColumbia University (BA)Princeton University (PhD)Oxford UniversityEra20th-century philosophyRegionWestern philosophySchoolAnalyticLibertarianismDoctoral advisorsCarl Gustav HempelMain interestsPolitical philosophy, ethics, epistemologyNotable ideasUtility monster, experience machine, ...

Zygmund redirects here. For people with similar names, see Zygmunt. Polish mathematician (1900–1992) Antoni ZygmundAntoni ZygmundBorn(1900-12-26)December 26, 1900Warsaw, Congress Poland, Russian EmpireDiedMay 30, 1992(1992-05-30) (aged 91)Chicago, Illinois, United StatesNationalityPolishCitizenshipPolish, AmericanAlma materUniversity of Warsaw (Ph.D., 1923)Known forSingular integral operatorsCalderón–Zygmund lemmaMarcinkiewicz–Zygmund inequalityPaley–Zygmund inequality...

ValueUnited StatesYears of minting1994ObverseDesignerT. James FerrellReverse Obverse Reverse The Thomas Jefferson 250th Anniversary silver dollar is a commemorative silver dollar issued by the United States Mint in 1994.[1] The obverse portrays Founding Father and United States president Thomas Jefferson and the words Architect of Democracy, and the reverse depicts Jefferson's Virginia home, Monticello. See also List of United States commemorative coins and medals (1990s) United State...

HarderwijkMunisipalitas / KotaCity gate, Harderwijk BenderaLambang kebesaranCountry NetherlandsProvinceGelderlandLuas(2006) • Total48,27 km2 (1,864 sq mi) • Luas daratan38,46 km2 (1,485 sq mi) • Luas perairan9,81 km2 (379 sq mi)Populasi (1 January, 2007) • Total42.057 • Kepadatan1.094/km2 (2,830/sq mi) Source: CBS, Statline.Zona waktuUTC+1 (CET) • Musim panas (DS...

Roman town destroyed by eruption of Mount Vesuvius For the modern Italian commune, see Ercolano. For other uses, see Herculaneum (disambiguation). HerculaneumThe excavations of HerculaneumShown within ItalyAlternative nameErcolanoLocationErcolano, Campania, ItalyCoordinates40°48′22″N 14°20′54″E / 40.8060°N 14.3482°E / 40.8060; 14.3482TypeSettlementHistoryFounded6th–7th century BCAbandoned79 ADSite notesWebsiteHerculaneum – Official website UNESCO W...

Bonifacio III del MonferratoMarchese del MonferratoStemma In carica1483 –1494 PredecessoreGuglielmo VIII SuccessoreGuglielmo IX Nascita10 agosto 1424 Morte1494 Casa realePaleologi PadreGiovanni Giacomo del Monferrato MadreGiovanna di Savoia ConiugiOrvietana FregosoElena di BrosseMaria Branković FigliGuglielmoGiangiorgio ReligioneCattolicesimo Marchesato del MonferratoPaleologi Teodoro I Figli Giovanni II Violante Giovanni II Figli Ottone III Giovanni III Teodoro II Margherita Ot...

1958 film Don Juan's Last AdventureDirected byMárton KeletiWritten byPéter SzászProduced byJózsef GoldaStarringZoltán Várkonyi Margit Bara Antal PágerCinematographyBarnabás HegyiEdited bySándor BoronkayMusic byTibor PolgárProductioncompanyHunnia FilmstúdióRelease date 11 December 1958 (1958-12-11) Running time92 minutesCountryHungaryLanguageHungarian Don Juan's Last Adventure (Hungarian: Don Juan legutolsó kalandja) is a 1958 Hungarian drama film directed by Márto...

Sergio Rubini alla 67ª Mostra internazionale d'arte cinematografica di Venezia (2010) Sergio Rubini (Grumo Appula, 21 dicembre 1959) è un attore, regista e sceneggiatore italiano. Indice 1 Biografia 2 Vita privata 3 Filmografia 3.1 Attore 3.1.1 Cinema 3.1.2 Televisione 3.2 Regista e sceneggiatore 4 Doppiaggio 5 Riconoscimenti 5.1 David di Donatello 5.2 Nastro d'argento 5.3 Globo d'oro 5.4 Ciak d'oro 6 Audiolibri 7 Discografia 7.1 Partecipazioni 8 Note 9 Altri progetti 10 Collegamenti estern...

Basilica di San Giovanni BattistaLa torre longobarda del VI secolo tra l'abside della Cappella di Teodolinda a sinistra e la sacrestia vecchia a destraStato Italia LocalitàMonza Coordinate45°35′00.83″N 9°16′31.58″E45°35′00.83″N, 9°16′31.58″E Religionecattolica di rito romano TitolareGiovanni Battista Arcidiocesi Milano Stile architettonicolongobardo Inizio costruzione595 circa Completamentofine VI secolo DemolizioneXIII-XIV secolo Modifica dati su Wikidata · Ma...

National beauty pageant competition in the Philippines For the most recent competition, see Miss Grand Philippines 2023. Miss Grand PhilippinesEstablished16 August 2014; 9 years ago (2014-08-16)FounderJohn Dela VegaTypeBeauty pageantHeadquartersManilaLocationPhilippinesMembership 2 (see Titles)Official language EnglishFilipinoPresident and National DirectorArnold L. Vegafria (2023 – Present)General ManagerAldrich Maru DabaoCreative Director and Head Fashion StylistFrancis ...