Парадокс Д’Аламбера
|
Read other articles:

Pelajar Meksiko yang mengambil pendidikan jarak jauh selama Pandemi COVID-19. Pendidikan jarak jauh (bahasa Inggris: distance education) adalah pendidikan formal berbasis lembaga yang peserta didik dan instrukturnya berada di lokasi terpisah sehingga memerlukan sistem telekomunikasi interaktif untuk menghubungkan keduanya dan berbagai sumber daya yang diperlukan di dalamnya. Pembelajaran elektronik (e-learning) atau pembelajaran daring (online) merupakan bagian dari pendidikan jarak jauh yang...

Alfred CapusNama dalam bahasa asli(fr) Alfred Capus BiografiKelahiran25 November 1858 Aix-en-Provence Kematian1r November 1922 (63 tahun)Neuilly-sur-Seine Tempat pemakamanPemakaman Père-Lachaise, 93 48°51′42″N 2°23′53″E / 48.861604°N 2.398129°E / 48.861604; 2.398129Grave of Capus (en) 16è Seat 24 of the Académie française (en) 12 Februari 1914 – 1r November 1922 ← Henri Poincaré – Édouard Estaunié → Data...
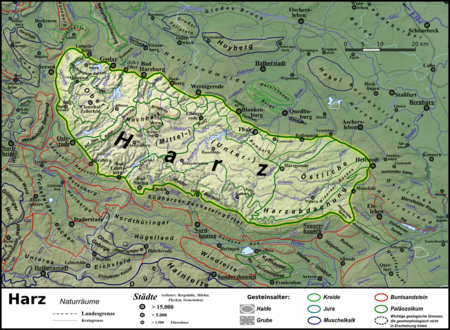
Upper HarzClausthal plateau in winterHighest pointPeakSchalkeElevation762 m (2,500 ft)GeographyHarz natural areas StateLower Saxony, GermanyRange coordinates51°49′N 10°22′E / 51.817°N 10.367°E / 51.817; 10.367Parent rangeHarzGeologyAge of rockPaleozoic (Devonian, Carboniferous) The Upper Harz (German: Oberharz, pronounced [ˈoːbɐhaːɐ̯ts]) is the northwestern and higher part of the Harz mountain range in Germany. The exact boundaries ...

1553 Franco-Ottoman invasion of Corsica Invasion of CorsicaPart of the Ottoman-Habsburg wars and the Italian War of 1551–1559Historic map of Corsica by Piri ReisDate1553–1559LocationCorsicaResult Ottomans and French temporarily occupy most of CorsicaBelligerents Republic of Genoa Ottoman Empire France CorsicansCommanders and leaders Andrea Doria Turgut Reis Paul de Thermes Paulin de la Garde Sampieru CorsuStrength 60 galleys 14 galleys vteItalian War of 1551–1559 T...

العلاقات الآيسلندية الباكستانية آيسلندا باكستان آيسلندا باكستان تعديل مصدري - تعديل العلاقات الآيسلندية الباكستانية هي العلاقات الثنائية التي تجمع بين آيسلندا وباكستان.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين:...

Colombian baseball stadium Estadio Édgar RenteríaAddressCalle 54 Número 40-224, Barranquilla, ColombiaLocationBarranquilla, Atlántico Department, ColombiaCoordinates10°59′42″N 74°47′04″W / 10.99495°N 74.784497°W / 10.99495; -74.784497OwnerCity of BarranquillaCapacity12,000[3]Field sizeLeft Field Line – 325 ft (99 m)Center Field – 400 ft (120 m)Right Field Line – 325 ft (99 m)SurfaceArtificial turfConstructionB...

CorinthiansNama lengkapSport Club Corinthians PaulistaJulukanTimão (The Great Team)Time do Povo (The People's Team)Todo Poderoso (Almighty)CoringãoBerdiri1 September 1910; 113 tahun lalu (1910-09-01)StadionArena Neo Química(Kapasitas: 49,205)PresidenDuílio Monteiro AlvesKepala pelatihFernando LázaroLigaCampeonato Brasileiro Série A Campeonato Paulista Série A12022 2022Série A, 4 dari 20 Paulistão, 3 dari 16Situs webSitus web resmi klub Kostum kandang Kostum tandang Kostum k...

Diploma Perang Kemerdekaan II Satyalancana Perang Kemerdekaan II adalah sebuah tanda kehormatan yang diberikan kepada anggota Angkatan Bersenjata yang mengikuti sepenuhnya peristiwa Perang Kemerdekaan I dari tanggal 18 Desember 1948 sampai dengan 27 Desember 1949, kecuali dalam hal mereka tertawan, mendapat luka-luka dan invalid. (Pasal 18 ayat 1 UU no.70/1958) Referensi (Indonesia) Penetapan Undang-undang Darurat No. 2 Tahun 1958 tentang Tanda-tanda Penghargaan untuk Anggota Angkatan Perang ...

Toyota StarletInformasiProdusenToyotaMasa produksi1973-1999Model untuk tahun1973-1999Bodi & rangkaKelasSubkompakKronologiPendahuluToyota PublicaPenerusToyota Yaris Toyota Starlet adalah mobil yang diproduksi oleh Toyota Motor Corporation, Japan dari tahun 1973 sampai 1999. Pada awalnya Starlet merupakan versi lebih mahal dari Toyota Publica, dan disebut Publica Starlet. Starlet yang sebenarnya (tanpa nama Publica) diluncurkan pada tahun 1978 berbentuk Hatchback 3 dan 5 pintu. Pasar y...

Sceaux 行政国 フランス地域圏 (Région) イル=ド=フランス地域圏県 (département) オー=ド=セーヌ県郡 (arrondissement) アントニー郡小郡 (canton) 小郡庁所在地INSEEコード 92071郵便番号 92330市長(任期) フィリップ・ローラン(2008年-2014年)自治体間連合 (fr) メトロポール・デュ・グラン・パリ人口動態人口 19,679人(2007年)人口密度 5466人/km2住民の呼称 Scéens地理座標 北緯48度4...

Canadian theatre director and producer Anderson c. 1915–20 John Murray Anderson (September 20, 1886 – January 30, 1954) was a Canadian theatre director and producer, songwriter, actor, screenwriter, dancer and lighting designer, who made his career in the United States, primarily in New York City and Hollywood. He worked in almost every genre of show business, including vaudeville, Broadway, and film. He also directed plays in London. Early life and education John Murray Anderson was born...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Tourism in Chhattisgarh – news · newspapers · books · scholar · JSTOR (October 2023) (Learn how and when to remove this message) Tourism is an important part of the economy of the Indian state of Chhattisgarh, India's tenth largest state. The state has many an...

Book by J.G. Ballard The 4-Dimensional Nightmare First editionAuthorJ. G. BallardCountryUnited KingdomLanguageEnglishGenreScience fictionPublisherVictor Gollancz LtdPublication date1963Media typePrint (hardback)Pages208 pp The 4-Dimensional Nightmare, also known as Voices of Time, is a collection of science fiction short stories by British writer J. G. Ballard, published in 1963 by Victor Gollancz. Contents The Voices of Time The Sound-Sweep Prima Belladonna Studio 5, The Stars The Garde...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: GNAT Modified General Public License – news · newspapers · books · scholar · JSTOR (December 2009) (Learn how and when to remove this message) The GNU logo The GNAT Modified General Public License (short: Modified GPL, GMGPL) is a version of the GNU General Pub...

English record producer, songwriter, broadcaster, and railway enthusiast For the boxer, see Peter Waterman. Pete WatermanOBE DLWaterman in 2014BornPeter Alan Waterman (1947-01-15) 15 January 1947 (age 77)[1]Coventry, Warwickshire, EnglandOccupationsRecord producersongwriterradio and club DJmusic managerbusinessmanbroadcasterrailway enthusiast (commercial)Years active1960s–presentTitle Chairman of Pete Waterman Entertainment (1984–present) President of Coventry Bears ...

Byproduct of coffee processing Coffee wastewater, also known as coffee effluent, is a byproduct of coffee processing. Its treatment and disposal is an important environmental consideration for coffee processing as wastewater is a form of industrial water pollution.[1] The unpicked fruit of the coffee tree, known as the coffee cherry, undergoes a long process to make it ready for consumption. This process often entails use of large quantities of water and the production of considerable...

Disambiguazione – Torneo di Aix-en-Provence rimanda qui. Se stai cercando Torneo maschile di tennis giocato ad Aix-en-Provence, vedi Aix-en-Provence Open. WTA Aix-en-Provence OpenSport Tennis CategoriaTier V (1988) FederazioneWomen's Tennis Association Paese Francia LuogoAix-en-Provence SuperficieTerra rossa OrganizzatoreWomen's Tennis Association CadenzaEdizione unica Partecipanti32M/32Q/16D StoriaFondazione1988 Soppressione1988 Numero edizioni1 Modifica dati su Wikidata ...

Burmese Buddhist deity ThagyaminKing of the Gods God of Lightning, Thunder, and Rain King of HeavenThe sculpture of Thagyamin in position of chief of nat in Shwezigon Pagoda in Pagan Kingdom. [1][2][3]Sanskrit transliterationShakrajAffiliationdeva, nat, Buddhism in Myanmar, Burmese folk religionAbodeAmarāvati, the capital of Indraloka (Indra's world) in Svarga,[4] Trāyastriṃśa (Heaven of the 33), Mount MeruWeaponVajra (Thunderbolt), Astras, Vasavi ShakthiS...

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 十二神将 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2019年10月) この十二神将には、一部のコンピュータや閲覧ソ...

Evaporation method This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Vapor-compression evaporation – news · newspapers · books · scholar · JSTOR (August 2016) (Learn ...