Задача Штейнера о минимальном дереве
| |||||||||
Read other articles:

Città metropolitana di Cataniacittà metropolitana Città metropolitana di Catania – VedutaPalazzo Minoriti, sede istituzionale LocalizzazioneStato Italia Regione Sicilia AmministrazioneCapoluogo Catania Sindaco metropolitanoEnrico Trantino (FdI) dal 6-6-2023[1] Data di istituzione4 agosto 2015 TerritorioCoordinatedel capoluogo37°31′N 15°04′E / 37.516667°N 15.066667°E37.516667; 15.066667 (Città metropolitana di Catania)Coordinate: 37...

Clara Jennifer Darren (lahir 4 November 1991) adalah seorang model dan aktris Indonesia yang populer melalui film Congklak Keramat tahun 2018 sebagai Dinda dan film Ajari Aku Islam dari Retro Pictures tahun 2019 sebagai Fau yang beradu akting dengan Roger Danuarta. Biografi Jennifer Darren terlahir kembar bersama Clementine Jessica Darren, anak dari pasangan orangtua Han Yuan Gunawan (ayah) (alm.) dan Lily (ibu). Ia adalah model Indonesia yang sebelumnya tinggal di Serang, Banten. Menyelesai...

Direct vote to replace an elected official before the end of their term Part of the Politics seriesDirect democracy Referendum types Optional referendum Legislative referral Popular initiative Recall referendum Popular referendum Mandatory referendum Referendums by country Australia Canada Czechia EU France Germany Italy Iran Israel Kenya Lithuania Netherlands New Zealand Poland Philippines Sweden Slovakia Switzerland Turkey Taiwan UK Ukraine USA Referendums by issue Civil rights Finance Mini...

Questa voce sugli argomenti società calcistiche argentine e provincia di San Juan è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Club Sportivo DesamparadosCalcio El Verde, Víboras, Los Puyutanos Segni distintivi Uniformi di gara Casa Trasferta Colori sociali Bianco, verde Dati societari Città San Juan Nazione Argentina Confederazione CONMEBOL Federazione AFA Campionato Torneo Argentino B Fondazione 1919 Presidente Ricardo Salvá Allenatore M...

Election in Tennessee Main article: 1824 United States presidential election 1824 United States presidential election in Tennessee ← 1820 October 26 – December 2, 1824 1828 → Nominee Andrew Jackson Party Democratic-Republican Home state Tennessee Running mate John C. Calhoun Electoral vote 11 Popular vote 20,197 Percentage 97.45% President before election James Monroe Democratic-Republican Elected President John Quincy Adams Democratic-Republ...
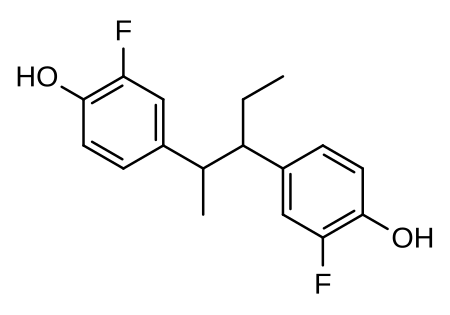
Mixture of two compounds BifluranolClinical dataTrade namesProstarexOther namesBX-341Drug classNonsteroidal estrogenIdentifiers IUPAC name 2-Fluoro-4-[3-(3-fluoro-4-hydroxyphenyl)pentan-2-yl]phenol CAS Number34633-34-6PubChem CID71713ChemSpider64763UNII47602X79JFChEBICHEBI:135219ChEMBLChEMBL2105524Chemical and physical dataFormulaC17H18F2O2Molar mass292.326 g·mol−13D model (JSmol)Interactive image SMILES CCC(C1=CC(=C(C=C1)O)F)C(C)C2=CC(=C(C=C2)O)F InChI InChI=1S/C17H18F2O2/c1-3-13(12-...

You can help expand this article with text translated from the corresponding article in Dutch. Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English Wikipedia. Consider adding a topic to this template: there are already 377 articles ...

Stasiun Sungai Tuha Bangunan baru Stasiun Sungai Tuha, Desember 2021LokasiTerukis Rahayu, Martapura, Ogan Komering Ulu Timur, Sumatera Selatan 32312IndonesiaKoordinat4°16′44″S 104°18′58″E / 4.27889°S 104.31611°E / -4.27889; 104.31611Koordinat: 4°16′44″S 104°18′58″E / 4.27889°S 104.31611°E / -4.27889; 104.31611Ketinggian+52 mOperator Kereta Api IndonesiaDivisi Regional IV Tanjungkarang Letakkm 201+011 lintas Panjang–Tanj...

This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. Please help improve this article by introducing more precise citations. (March 2013) (Learn how and when to remove this message) Memorial in honour of State Defense Guard at state border in Lusatian Mountains State Defense Guard (in Czech Stráž obrany státu, SOS, in Slovak Stráž obrany štátu) was a military service established in 1936 to prot...

В этом китайском имени фамилия (Дуань) стоит перед личным именем. Дуань Цижуйкит. трад. 段祺瑞 Президент Китайской республики 1 июля — 13 июля 1917 Предшественник Ли Юаньхун Преемник Ли Юаньхун 24 ноября 1924 — 20 апреля 1926 Предшественник Хуан Фу Преемник Ху Вэйдэ Председате...

Deck gun 5/38 caliber gun Two Mk 30 single enclosed base ring mounts on USS David W. TaylorTypeDeck gunPlace of originUnited StatesService historyIn service1934–2008Used byUnited States Navy, United States Coast Guard, Royal Navy, Danish Navy, Italian Navy, Japan Maritime Self-Defense Force, South Vietnamese Navy, and every navy that bought surplus World War II, US Navy warshipsWarsWorld War II, Korean War, Vietnam War, Gulf War, Falklands War, and wars that involv...

معركة ملاذكردنبرد ملازگرد جزء من الحروب السلجوقية – البيزنطية منمنمة فرنسية تعود إلى منتصف القرن الخامس عشر تصور معركة ملاذكرد، يرتدي المقاتلون الدرع الأوروبي الغربي الحديث. معلومات عامة التاريخ 26 أغسطس 1071/الجمعة 28 ذي القعدة 463 هـ البلد تركيا الموقع بالقرب من ملاذكرد...

U.S. Real Estate Investment Trust Store Capital CorporationCompany typePrivateTraded asNYSE: STOR(2015–2023)IndustryReal estate investment trust (REIT)Founded2011; 13 years ago (2011)HeadquartersScottsdale, Arizona, U.S.Key peopleMary Fedewa (CEO) Sherry Rexroad (CFO)ServicesReal Estate leasesRevenue US$783.8 million (2021)Net income US$268.35 million (2021)Total assets US$9.7 billion (2021)Total equity US$5.1 billion (2021)OwnerGICOak Street Capit...

Le informazioni riportate non sono consigli medici e potrebbero non essere accurate. I contenuti hanno solo fine illustrativo e non sostituiscono il parere medico: leggi le avvertenze. Somministrazione orale. La somministrazione orale (anche detta per via orale o per os) è una via di somministrazione di una sostanza e indica che un farmaco deve essere somministrato per bocca. Spesso i medici per indicare questa via di somministrazione sono soliti abbreviare PO sulle ricette e prescrizioni m...

Orang CornwallJumlah populasi6–11 juta di seluruh dunia[1][2] Populasi Cornwall dari Sensus Britania Raya 2011 532.300; 83.966 menyatakan identitas nasional mereka sebagai orang Cornwall di Sensus Britania Raya 2011 (73.220 di Cornwall, 14% populasi);[3][4] 26% populasi Cornwall diidentifikasi sebagai orang Cornwall dalam Survei Kualitas Kehidupan Cornwall 2007;[5] 28.584 – 41% murid sekolah di Cornwall tercatat berasal dari orang Cornwall pada tahu...

Vinko RadićNazionalità Jugoslavia Croazia (dal 1941) Calcio RuoloCentrocampista Termine carriera1929 CarrieraSquadre di club1 1920-1929 Hajduk Spalato20 (6) Nazionale 1924-1927 Jugoslavia3 (0) 1 I due numeri indicano le presenze e le reti segnate, per le sole partite di campionato.Il simbolo → indica un trasferimento in prestito. Modifica dati su Wikidata · Manuale Vinko Radić (Spalato, 2 febbraio 1898 – Spalato, 9 ottobre 1945) è stato un calciatore jugosl...

Cet article est une ébauche concernant une athlète péruvienne. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Kimberly GarcíaBiographieNaissance 19 octobre 1993 (30 ans)HuancayoNationalité péruvienneActivités Athlète, marcheuseAutres informationsTaille 1,64 mPoids 51 kgSport AthlétismeDisciplines sportives 20 kilomètres marche, 35 kilomètres marcheDistinction Laureles Deportivos (d)modifier - mo...

Austrian composer, teacher and pianist (1765–1807) Anton Franz Josef Eberl[1] (13 June 1765 – 11 March 1807)[2] was an Austrian composer, teacher and pianist of the Classical period. He was a student of Salieri and Mozart. He was also seen as an early friend and rival of Beethoven. Biography Eberl was born in Vienna, Austria in 1765, the son of a wealthy imperial official. He was a gifted pianist who gave recitals in Vienna from the age of eight. The family eventually fell...
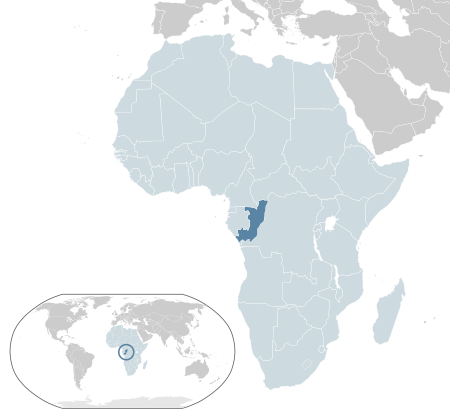
Ethno-political conflict in the Republic of the Congo For the 1998–2003 war in the Democratic Republic of the Congo, see Second Congo War. Second Republic of the Congo Civil WarPart of the aftermaths of the First Congo War and Rwandan genocideDate5 June 1997 – 29 December 1999[1](2 years, 6 months and 24 days)LocationRepublic of the CongoResult Nguesso loyalist victory Denis Sassou Nguesso returns to powerBelligerents Armed Forces of the Republic of the Congo (to Oc...

この存命人物の記事には検証可能な出典が不足しています。 信頼できる情報源の提供に協力をお願いします。存命人物に関する出典の無い、もしくは不完全な情報に基づいた論争の材料、特に潜在的に中傷・誹謗・名誉毀損あるいは有害となるものはすぐに除去する必要があります。出典検索?: 十朱幸代 – ニュース · 書籍 · スカラー · CiNii ...


























































![{\displaystyle [G,\varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e1d197b9e9a672ea175efeaa153a9e2ac1d47cb)
![{\displaystyle \operatorname {mpn} [G,\varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8769b1e78e4f3c6b89c2a89f46abeac27515147)

![{\displaystyle \Gamma \in [G,\varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8feeafde16a1aa862a160854904d344120461895)
![{\displaystyle \operatorname {smt} (M)=\inf \operatorname {mpn} [G,\varphi ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8854ead749a415e697bce3ee088d37163897e197)












