Алгоритмы быстрого возведения в степень
|
Read other articles:

Peta menunjukkan lokasi Candelaria Candelaria adalah munisipalitas yang terletak di provinsi Quezon, Filipina. Pada tahun 2010, munisipalitas ini memiliki populasi sebesar 113.514 jiwa dan 23.227 rumah tangga. Pembagian wilayah Secara administratif Candelaria terbagi menjadi 25 barangay, yaitu: Bukal Norte Bukal Sur Buenavista East Buenavista West Kinatihan I Kinatihan II Malabanban Norte Malabanban Sur Mangilag Norte Mangilag Sur Masalukot I Masalukot II Masalukot III Masalukot IV Masalukot ...

Keuskupan AvezzanoDioecesis MarsorumKatolik Katedral AvezzanoLokasiNegara ItaliaProvinsi gerejawiL'AquilaStatistikLuas1.700 km2 (660 sq mi)Populasi- Total- Katolik(per 2006)115.137109,000 (94.7%)Paroki95InformasiDenominasiGereja KatolikRitusRitus RomaPendirianAbad ke-9KatedralKatedral Santo Bartolomeus Rasul (Avezzano)KonkatedralKonkatedral Santa Maria Bunda Rahmat (Pescina)Kepemimpinan kiniPausFransiskusUskupPietro SantoroPetaSitus webwww.diocesidiavez...

University in Kenya This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: Moi University – news · newspapers · books · scholar · JSTOR (June 2017) (Learn how and when to remove this template message) Moi UniversityMottoFoundation of knowledgeTypePublic UniversityEstablished1984; 40 years ago (1984)FounderDaniel arap MoiBudget6.93 Billion KSH...

Pamflet Perdjoeangan Rakjat di Yogyakarta Pamflet atau Sebaran Lipat (atau dapat juga disebut selebaran, sebaran, risalah, tebaran[1]) adalah tulisan yang dapat disertai dengan gambar atau tidak, tanpa penyampulan maupun penjilidan, yang dicantumkan pada selembar kertas di satu sisi atau kedua sisinya, lalu dilipat atau dipotong setengah, sepertiga, atau bahkan seperempatnya, sehingga terlihat lebih kecil. Pamflet dapat pula terdiri dari beberapa lembar kertas yang dilipat atau disatu...

Ini adalah nama Batak Toba, marganya adalah Panjaitan. Trimedya PanjaitanS.H., M.H. Anggota Dewan Perwakilan Rakyat Republik IndonesiaPetahanaMulai menjabat 28 Mei 2002[1]Pengganti Antar Waktu hingga 30 September 2004 PendahuluGusti Basan BurniaPenggantiPetahanaDaerah pemilihanSumatera Utara II Informasi pribadiLahir6 Juni 1966 (umur 57)Medan, Sumatera Utara, IndonesiaKebangsaanIndonesiaPartai politikPDI-PSuami/istriJovita Eva Sasantie SiwiAnak3Alma materUniversitas Pancasila...

Artikel atau sebagian dari artikel ini mungkin diterjemahkan dari Rapid transit di en.wikipedia.org. Isinya masih belum akurat, karena bagian yang diterjemahkan masih perlu diperhalus dan disempurnakan. Jika Anda menguasai bahasa aslinya, harap pertimbangkan untuk menelusuri referensinya dan menyempurnakan terjemahan ini. Anda juga dapat ikut bergotong royong pada ProyekWiki Perbaikan Terjemahan. (Pesan ini dapat dihapus jika terjemahan dirasa sudah cukup tepat. Lihat pula: panduan penerjemah...

Apartment building in Manhattan, New York United States historic place360 Central Park WestU.S. Historic districtContributing property Show map of New York CityShow map of New YorkShow map of the United StatesLocationManhattan, New York City, New York United StatesCoordinates40°47′30″N 73°57′55″W / 40.791605°N 73.965199°W / 40.791605; -73.965199Built1928 (1928)ArchitectRosario CandelaArchitectural styleNeo-RenaissancePart ofCentral Park West...

Посольство Японии в Российской Федерациияп. 在ロシア日本国大使館 Япония Россия Местоположение Басманный район, Москва Адрес Грохольский пер., 27 Посол Акира Муто Сайт ru.emb-japan.go.jp Медиафайлы на Викискладе Посольство Японии в Москве (яп. 在ロシア日本国大使館) — дипломатическа�...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

Confederations CupSport Calcio TipoNazionali CategoriaMaschile OrganizzatoreFIFA CadenzaQuadriennale AperturaGiugno ChiusuraLuglio Partecipanti8 FormulaGironi + play-off StoriaFondazione1992 Soppressione2017 Numero edizioni10 Ultimo vincitore Germania Record vittorie Brasile (4) Trofeo o riconoscimento Modifica dati su Wikidata · Manuale La Confederations Cup è stata una competizione calcistica per nazionali maschili organizzata dalla FIFA tra il 1992 e il 2017.[1] Tenutasi sto...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

American author (1927–2020) For the Michigan politician, see Roger Kahn (politician). For the American musician and composer, see Roger Wolfe Kahn. Not to be confused with Roger Angell. Roger KahnBorn(1927-10-31)October 31, 1927New York City, U.S.DiedFebruary 6, 2020(2020-02-06) (aged 92)Mamaroneck, New York, U.S.OccupationAuthorNationalityAmericanNotable worksThe Boys of Summer Roger Kahn (October 31, 1927 – February 6, 2020) was an American author, best known for his 1972 baseball ...

SMK Negeri 3 DepokInformasiDidirikan04 Juni 2012JenisNegeriAkreditasiA[1]Nomor Statistik Sekolah32102761016Nomor Pokok Sekolah Nasional20276188Kepala SekolahSamsuri S.Pd, MMJumlah kelasX: 10, XI: 10, XII: 10Jurusan atau peminatan6 JurusanRentang kelasX, XI, XIIKurikulumKurikulum 2013StatusSekolah Standar NasionalAlamatLokasi Gedung A: Jalan H. Tabroni №74, Kalimulya, Kec. Cilodong, Depok, Jawa Barat, Indonesia Gedung B: Jalan Merdeka №128, Abadi Jaya, Kec. Sukmajaya, Dep...

The Right HonourableThe Lord TweedsmuirCBE CD FRSE FRSABaron TweedsmuirIn office11 February 1940 – 20 June 1996Preceded byJohn BuchanSucceeded byWilliam Buchan Personal detailsBorn25 November 1911Died20 June 1996(1996-06-20) (aged 84)Spouse(s)Priscilla Grant (died 1978) Lady Jean Grant (m. 1980)Parent(s)John Buchan, 1st Baron Tweedsmuir Susan Charlotte GrosvenorAlma materEton College Brasenose College, Oxford John Norman Stuart Buchan, 2nd Baron...

British diver Chris Mears MBEChris Mears at the 2016 Olympics in RioPersonal informationFull nameChristopher James MearsNicknameChrisBorn (1993-02-07) 7 February 1993 (age 31)Reading, BerkshireHeight1.74 m (5 ft 9 in)SportCountry Great Britain EnglandSportDivingEvent(s)1m, 3m, 3m SynchroClubCity of Leeds Diving Club Medal record Representing Great Britain Olympic Games 2016 Rio de Janeiro 3 m synchro World Championships 2015 Kazan 3 m synchro European ...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Maret 2016. Artikel ini perlu dikembangkan agar dapat memenuhi kriteria sebagai entri Wikipedia.Bantulah untuk mengembangkan artikel ini. Jika tidak dikembangkan, artikel ini akan dihapus. Makam di Odel pada tahun 1915-1926 Odel adalah sebuah desa di Kota Serang, pr...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Layang-Layang, Johor – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this message) Layang-Layang is a town in Kluang District, Johor, Malaysia. It is situated within the parliamentary constituency of Simpang Renggam. It is located appro...

« Bataille de Saint-Aubin-du-Cormier » redirige ici. Pour les autres significations, voir Bataille de Saint-Aubin-du-Cormier (homonymie). Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (décembre 2008). Vous pouvez améli...

Type of volcanic arc occurring along a continental margin A continental arc is a type of volcanic arc occurring as an arc-shape topographic high region along a continental margin. The continental arc is formed at an active continental margin where two tectonic plates meet, and where one plate has continental crust and the other oceanic crust along the line of plate convergence, and a subduction zone develops. The magmatism and petrogenesis of continental crust are complicated: in essence, con...
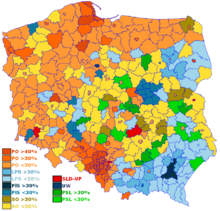
2004 European Parliament election in Poland 13 June 2004 2009 → 54 seats to the European ParliamentTurnout20.87% First party Second party Third party Leader Jerzy Buzek Mirosław Piotrowski Anna Fotyga Party PO LPR PiS Alliance EPP IND/DEM AEN Seats won 15 seats 10 seats 7 seats Popular vote 1,467,775 969 689 771 858 Percentage 24.1% 15.92% 12.67% Fourth party Fifth party Sixth party Leader Ryszard Czarnecki Lidia Geringer de Oedenberg Władys...










































