–Р–і–і–Є—В–Є–≤–љ–∞—П —В–µ–Њ—А–Є—П —З–Є—Б–µ–ї
|
Read other articles:

Kitakyushu City General GymnasiumNama lengkapKitakyushu City General GymnasiumLokasiYahatahigashi-ku, Kitaky≈Ђsh≈Ђ, JepangPemilikKitakyushu cityOperatorKitakyushu cityKapasitas10,000KonstruksiDibuka12 Januari, 1974BiayaгААArsitekYamashita Sekkei Inc. Kitakyushu City General Gymnasium sebuah arena di Kitakyushu, Fukuoka, Jepang.[1] Lewat satelit Referensi ^ еЕђзЫКи≤°еЫ£ж≥ХдЇЇ еМЧдєЭеЈЮеЄВдљУиВ≤еНФдЉЪ (March 2018). дљУиВ≤еНФдЉЪдЇЛеЛЩе±А пЉИзЈПеРИдљУиВ≤駮еЖЕпЉЙ. Diarsipkan dari versi as...

Sebuah pesawat udara Panavia Tornado ECR milik Jerman, 22 September 1997. Pesawat udara (bahasa Inggris: Aircraft) adalah setiap mesin atau alat yang dapat terbang di atmosfer karena gaya angkat dari reaksi udara, tetapi bukan karena reaksi udara terhadap permukaan bumi yang digunakan untuk penerbangan.[1] Pesawat udara mencakup pesawat terbang atau pesawat bersayap tetap dan helikopter atau diartikan pesawat udara yang lebih berat dari udara, bersayap putar yang rotornya digerakkan o...

Kejadian 27Sebuah halaman dari Kodeks Aleppo, difoto pada tahun 1887 oleh William Wickes, memuat Kejadian 26:35 („Ф„Ч„™„Щ) sampai 27:30 („Х„Щ„Ф„Щ „Р„Ъ). Menunjukkan adanya pemisah parashah terbuka tunggal {S} pada 27:1 („Х„Щ„Ф„Щ „Ы„Щ „Ц„І„Я „Щ„¶„Ч„І) sebagai sub-bagian Parashat ToledotKitabKitab KejadianKategoriTauratBagian Alkitab KristenPerjanjian LamaUrutan dalamKitab Kristen1← pasal 26 pasal 28 → Kejadian 27 (disingkat Kej 27) adalah bagian dari Kitab Kejadian dalam Alkitab Ib...

ўДўЕЎєЎІўЖўН Ў£ЎЃЎ±ўЙЎМ ЎЈЎІўДЎє Ў±ўКЎ™ЎіЎІЎ±Ўѓ Ў±ўИЎ®Ў±Ў™Ў≥ (Ў™ўИЎґўКЎ≠). Ў±ўКЎ™ЎіЎІЎ±Ўѓ Ў±ўИЎ®Ў±Ў™Ў≥ ўЕЎєўДўИўЕЎІЎ™ ЎіЎЃЎµўКЎ© ЎІЎ≥ўЕ ЎІўДўИўДЎІЎѓЎ© (Ў®ЎІўДЎ•ўЖЎђўДўКЎ≤ўКЎ©: Richard John Roberts)вАП ЎІўДўЕўКўДЎІЎѓ 6 Ў≥Ў®Ў™ўЕЎ®Ў± 1943 (81 Ў≥ўЖЎ©)[1] ЎѓўКЎ±Ў®ўК ўЕўИЎІЎЈўЖЎ© ЎІўДўЕўЕўДўГЎ© ЎІўДўЕЎ™Ў≠ЎѓЎ© ЎєЎґўИ ўБўК ЎІўДўЕўЖЎЄўЕЎ© ЎІўДЎ£ўИЎ±ўИЎ®ўКЎ© ўДўДЎ®ўКўИўДўИЎђўКЎІ ЎІўДЎђЎ≤ўКЎ¶ўКЎ© [ўДЎЇЎІЎ™ Ў£ЎЃЎ±ўЙ]ЎМ ўИЎІўДЎ£ўГпњљ...

Fifth major version of the Android operating system Android LollipopVersion of the Android operating systemScreenshotAndroid Lollipop home screenDeveloperGoogleGeneralavailabilityNovember 4, 2014; 9 years ago (2014-11-04)[1]Final release5.1.1_r38 (LMY49M)[2] / July 5, 2016; 7 years ago (2016-07-05)[3]Kernel typeMonolithic (Linux)Preceded byAndroid 4.4.4 KitKatSucceeded byAndroid 6.0 MarshmallowOfficial websitewww.android.com/versions...

Hindu temple in Karnataka, IndiaKedareshvara TempleHindu templeKedareshvara temple (1070) at Balligavi in Shimoga districtCountry IndiaStateKarnatakaDistrictShimoga DistrictLanguages вАҐ OfficialKannadaTime zoneUTC+5:30 (IST) The Kedareshvara temple (also spelt Kedareshwara or Kedaresvara) is located in the town of Balligavi (known variously in ancient inscriptions as Belagami, Belligave, Ballagamve and Ballipura), near Shikaripura in the Shimoga district of Karnataka state, I...

Malaysian medical officer and spaceflight participant (born 1972) You can help expand this article with text translated from the corresponding article in Malay. (April 2016) Click [show] for important translation instructions. View a machine-translated version of the Malay article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simpl...

Wauwatosacity(EN) Wauwatosa, Wisconsin Wauwatosa вАУ Veduta LocalizzazioneStato Stati Uniti Stato federato Wisconsin ConteaMilwaukee AmministrazioneSindacoJill Didier TerritorioCoordinate43¬∞03вА≤32вА≥N 88¬∞01вА≤34вА≥W / 43.058889¬∞N 88.026111¬∞W43.058889; -88.026111пїњ (Wauwatosa)Coordinate: 43¬∞03вА≤32вА≥N 88¬∞01вА≤34вА≥W / 43.058889¬∞N 88.026111¬∞W43.058889; -88.026111пїњ (Wauwatosa) Altitudine205 m s.l.m. Superficie21,24 km¬≤ Abitanti44&#...

1985 Invincible-class light aircraft carrier For other ships with the same name, see HMS Ark Royal. HMS Ark Royal alongside at Portsmouth in 2007 History United Kingdom NameArk Royal NamesakeThe 1587 flagship that defeated the Spanish Armada in 1588, Ark Royal OrderedDecember 1978 BuilderSwan Hunter, Tyne and Wear, United Kingdom Laid down14 December 1978 Launched2 June 1981 Sponsored byQueen Elizabeth The Queen Mother Commissioned1 November 1985 Decommissioned11 March 2011[2][3&#...

–Я—А–µ—Б—В–Њ–ї—М–љ—Л–є –њ—А–∞–Ј–і–љ–Є–Ї –Ш. –Ь. –Я—А—П–љ–Є—И–љ–Є–Ї–Њ–≤. –Ю–±—Й–Є–є –ґ–µ—А—В–≤–µ–љ–љ—Л–є –Ї–Њ—В—С–ї –≤ –њ—А–µ—Б—В–Њ–ї—М–љ—Л–є –њ—А–∞–Ј–і–љ–Є–Ї. –Э–∞—З–∞–ї–Њ 1890-—Е –Ґ–Є–њ —Е—А–Є—Б—В–Є–∞–љ—Б–Ї–Є–є / –љ–∞—А–Њ–і–љ–Њ-—Е—А–Є—Б—В–Є–∞–љ—Б–Ї–Є–є –Ш–љ–∞—З–µ —Е—А–∞–Љ–Њ–≤—Л–є, —З–∞—Б–Њ–≤–µ–љ–љ—Л–є, —Б—К–µ–Ј–ґ–Є–є, –≥—Г–ї—С–≤—Л–є –њ—А–∞–Ј–і–љ–Є–Ї –Ч–љ–∞—З–µ–љ–Є–µ –њ—А–∞–Ј–і–љ–Є–Ї —Б–µ–ї–∞ –Є–ї–Є –њ—А–Є—Е–Њ–і–∞ –Ю—В–Љ–µ—З–∞–µ—В—Б—П —Е—А–Є—Б—В–Є–∞–љ–∞–Љ–Є –Ґ—А–∞–і–Є—Ж–Є–Є –Ї—А–µ—Б—В–љ—Л–є пњљ...

SMK Negeri 13 BandungSMT Kimia Bandung Sekolah Analis Kimia ITBInformasiDidirikan 16 September 1938 (Sekolah Analis Kimia ITB) 07 Maret 1988(SMT Kimia Bandung) 07 Maret 1997(SMKN 13 Bandung) JenisKejuruanAkreditasiANomor Pokok Sekolah Nasional20219161Kepala SekolahProf.Dr.Schaeffer M.PdJumlah kelas39Jurusan atau peminatan Analis Kimia Teknik Komputer Jaringan Rekayasa Perangkat Lunak Rentang kelas X AK, TKJ, RPL XI AK, TKJ, RPL XII AK, TKJ, RPL XIII AK KurikulumKurikulum 2013StatusN...

Former French university in Montepllier, founded in 1971, replaced and abolished in 2015 This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: University of Montpellier 1 вАУ news ¬Ј newspapers ¬Ј books ¬Ј scholar ¬Ј JSTOR (July 2015) (Learn how and when to remove this message) Montpellier 1 UniversityUniversit√© Montpellier 1Logo of Mon...
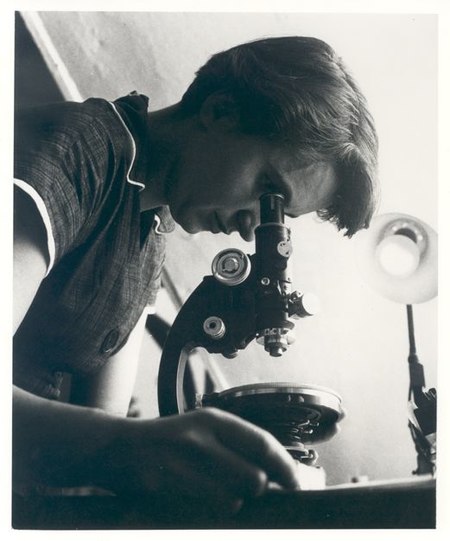
British X-ray crystallographer (1920вАУ1958) This article is about the chemist. For the Mars rover named after her, see Rosalind Franklin (rover). Rosalind FranklinBornRosalind Elsie Franklin(1920-07-25)25 July 1920Notting Hill, London, EnglandDied16 April 1958(1958-04-16) (aged 37)Chelsea, London, EnglandResting placeWillesden United Synagogue Cemetery51¬∞32вА≤41вА≥N 0¬∞14вА≤24вА≥W / 51.5447¬∞N 0.2399¬∞W / 51.5447; -0.2399EducationSt Paul's Girls' SchoolAlma ...

Network Rail A Class 158 diesel multiple unit Diesel multiple units and railcars are trains, usually with passenger accommodation, that do not require a locomotive. Railcars can be single cars, while in multiple units cars are marshalled together with a driving position either end. As of December 2010[update], 23 percent of the rail passenger cars used on Network Rail are part of a diesel multiple unit. Some prototype steam-powered railcars appeared in the mid-19th century, and a...

American politician (born 1956) French HillMember of the U.S. House of Representativesfrom Arkansas's 2nd districtIncumbentAssumed office January 3, 2015Preceded byTim Griffin Personal detailsBornJames French Hill (1956-12-05) December 5, 1956 (age 67)Little Rock, Arkansas, U.S.Political partyRepublicanSpouse Martha McKenzie (m. 1988)Children2EducationVanderbilt University (BA)WebsiteHouse website French Hill's voice French Hill pays tribute...

Part of the LGBT rights seriesLegal status ofsame-sex unions Marriage Andorra Argentina Australia Austria Belgium Brazil Canada Chile Colombia Costa Rica Cuba Denmark Ecuador Estonia Finland France Germany Greece Iceland Ireland Liechtenstein* Luxembourg Malta Mexico Nepal Netherlands1 New Zealand2 Norway Portugal Slovenia South Africa Spain Sweden Switzerland Taiwan United Kingdom3 United States4 Uruguay Recognized Israel5 Civil unions andregistered partnerships Bolivia Croatia Cyprus Czech...

Gondang buhun merupakan salah satu jenis tradisi Gondang berupa seni tetabuhan (tutunggulan) yang berasal dari Kampung Adat Kuta, Ciamis, Jawa Barat yang tidak terdapat pada daerah lain. Dalam pelaksanaannya, seluruh pemain Gondang Buhun ini semuanya harus perempuan[1] sebagai pemukul lesung (gondang) yang juga merangkap sebagai juru kawih (sinden).[2] Instrumen yang mereka gunakan berupa alu yang tingginya mencapai 2 meter, dan lesung yang panjangnya 2,5 meter berisi dua ikat...

Most common stainless steel 18/10 redirects here. For the date, see October 18. Staybrite redirects here. For Zenith Staybrite windows, see Brian Kennedy (businessman) ¬І Business. 304 stainless steel pipes. SAE 304 stainless steel is the most common stainless steel. It is an alloy of iron, carbon, chromium and nickel. It is an austenitic stainless steel, and is therefore not magnetic. It is less electrically and thermally conductive than carbon steel. It has a higher corrosion resistanc...

2019 EuropeanWrestling ChampionshipsFreestyleGreco-RomanWomen57 kg55 kg50 kg61 kg60 kg53 kg65 kg63 kg55 kg70 kg67 kg57 kg74 kg72 kg59 kg79 kg77 kg62 kg86 kg82 kg65 kg92 kg87 kg68 kg97 kg97 kg72 kg125 kg130 kg76 kgvte Main article: 2019 European Wrestling Championships The men's freestyle 86 kg is a competition featured at the 2019 European Wrestling Championships, and was held in Bucharest, Romania on April 9 and April 10. Medalists Gold Vladislav Valiev Russia Silver Piotr Ianulov...

–£ —Н—В–Њ–≥–Њ —В–Њ–њ–Њ–љ–Є–Љ–∞ –µ—Б—В—М –Є –і—А—Г–≥–Є–µ –Ј–љ–∞—З–µ–љ–Є—П, —Б–Љ. –Ч–∞—А–µ—З—М–µ. –Ф–µ—А–µ–≤–љ—П–Ч–∞—А–µ—З—М–µ 56¬∞29вА≤40вА≥ —Б. —И. 35¬∞59вА≤29вА≥ –≤. –і.HG–ѓO –°—В—А–∞–љ–∞ –†–Њ—Б—Б–Є—П –°—Г–±—К–µ–Ї—В –§–µ–і–µ—А–∞—Ж–Є–Є –Ґ–≤–µ—А—Б–Ї–∞—П –Њ–±–ї–∞—Б—В—М –Ь—Г–љ–Є—Ж–Є–њ–∞–ї—М–љ—Л–є —А–∞–є–Њ–љ –Ъ–∞–ї–Є–љ–Є–љ—Б–Ї–Є–є –°–µ–ї—М—Б–Ї–Њ–µ –њ–Њ—Б–µ–ї–µ–љ–Є–µ –Ґ—Г—А–≥–Є–љ–Њ–≤—Б–Ї–Њ–µ –Ш—Б—В–Њ—А–Є—П –Є –≥–µ–Њ–≥—А–∞—Д–Є—П –І–∞—Б–Њ–≤–Њ–є –њ–Њ—П—Б UTC+3:00 –Э–∞—Б–µ–їпњљ...







