Read other articles:

Tonga padaOlimpiadeKode IOCTGAKONKomite Olimpiade Nasional dan Asosiasi Olahraga TongaSitus webwww.oceaniasport.com/tongaMedali 0 1 0 Total 1 Penampilan Musim Panas1984198819921996200020042008201220162020Penampilan Musim Dingin201420182022 Tonga telah berkompetisi dalam delapan edisi Olimpiade Musim Panas dan dua Olimpiade Musim Dingin. Tonga menjadi negara independen terkecil yang memenangkan sebuah medali Olimpiade dalam permainan musim panas saat petinju kelas berat super Paea Wolfgramm me...

AlboinRaja LombardiaSketsa ukiran kayu Alboin pada tahun 1493 Kronik NurembergBerkuasaskt. 560/565 – 572PendahuluHildwinPenerusClefiKelahiran530-anPannoniaKematian28 Juni 572Verona, AustriaKerajaan LombardiaPemakamanVeronaWangsaWangsa GausiAyahHildwinIbuRodelindaPasanganClodosvinta RosamundaAnakAlbsuindaAgamaArianisme Alboin (530an – 28 Juni 572) merupakan raja Lombardia dari sekitar tahun 560 sampai 572. Selama pemerintahannya Lombardia mengakhiri migrasi dengan menetap di Italia, bagian...

Halaman ini berisi artikel tentang sistem abad pertengahan. Untuk sistem abad ke-17 di Kanada, lihat Sistem seigneurial dari Prancis Baru. Les Très Riches Heures du Duc de Berry, s.1410 Manorialisme adalah sebuah unsur esensial dari masyarakat feodal.[1] Ini adalah prinsip penghimpunan ekonomi desa yang bermula dalam sistem vila Romawi dari Kekaisaran Romawi Akhir,[2] dan banyak diterapkan di barat dan sebagian tengah Eropa pada Abad Pertengahan. Ini perlahan digantikan oleh ...

Untuk kegunaan lain, lihat Spitz (disambiguasi). Spitz adalah sebutan untuk berbagai jenis anjing ras yang memiliki ciri khas bulu tebal dan panjang, serta daun telinga yang agak kecil dan berdiri. Ekor berbulu lebat dan melengkung ke arah punggung. Dalam bahasa Jerman, spitz antara lain berarti runcing atau tajam. Anjing spitz cocok hidup di belahan bumi utara yang beriklim dingin. Bulu anjing spitz bagaikan mantel berlapis dua. Lapisan bulu sebelah dalam lebih rapat daripada lapisan bulu ba...

Badan Rumah Tangga Kekaisaran宮内庁Kunai-chōGedung Badan Rumah Tangga Kekaisaran di halaman Istana Kekaisaran di Chiyoda, TokyoInformasi lembagaDibentuk1 Juni 1949 (1949-06-01)Nomenklatur sebelumnyaKantor Rumah Tangga Kekaisaran (1947-1949)Kementerian Rumah Tangga Kekaisaran (701-1947)Wilayah hukum JepangKantor pusat1-1 Chiyoda, Chiyoda-ku, Tokyo 100-8111, JepangPegawai1,053Anggaran tahunan¥17,766M(FY 2007)Pejabat eksekutifYasuhiko Nishimura, Kepala pengurusKenji Ikeda, Wakil k...

Urho Castrén Perdana Menteri FinlandiaMasa jabatan21 September 1944 – 17 November 1944 PendahuluAntti HackzellPenggantiJuho Kusti Paasikivi Informasi pribadiLahir30 Desember 1886JyväskyläMeninggal8 Maret 1965(1965-03-08) (umur 78)Partai politikPartai Koalisi NasionalSunting kotak info • L • B Urho Jonas Castrén (30 Desember 1886, Jyväskylä – 8 Maret 1965) adalah seorang politikus Finlandia dari Partai Koalisi Nasional. Ia menjadi Perdana Menteri Finlandia...

Об экономическом термине см. Первородный грех (экономика). ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Ран�...

1984 film by Dennis Shryack Not to be confused with Flash Point (film). FlashpointTheatrical release posterDirected byWilliam TannenWritten byDennis ShryackMichael ButlerBased onFlashpointby George LaFountaine[1]Starring Kris Kristofferson Treat Williams Rip Torn Tess Harper CinematographyPeter MossEdited byDavid GarfieldMusic byTangerine DreamProductioncompaniesHBO PicturesSilver Screen PartnersDistributed byTri-Star PicturesRelease date August 31, 1984 (1984-08-31) Ru...

Pour un article plus général, voir Tour de France 2021. 6e étape du Tour de France 2021 GénéralitésCourse6e étape، Tour de France 2021Type Étape de plaineDate1 juillet 2021Distance160,6 kmPays FranceLieu de départToursLieu d'arrivéeChâteaurouxPartants177Arrivants177Vitesse moyenne48,765 km/hDénivelé926 mRésultats de l’étape1er Mark Cavendish3 h 17 min 36 s(Deceuninck-Quick Step)2e Jasper Philipsen+ 0 s3e Nacer Bouhanni+ 0 s Greg Van Avermaet(AG2R Citroën Team)Classement g�...

Grafik fungsi dengan asimtot horizontal (y = 0), vertikal (x = 0), dan miring (garis ungu, diberikan oleh y = 2x) Kurva yang memotong suatu asimtot berkali-kali sebanyak takhingga Dalam geometri analitis, asimtot dari sebuah kurva adalah sebuah garis yang sedemikian rupa sehingga jarak antara kurva dan garis tersebut mendekati nol seiring x atau y (salah satu atau keduanya) mendekati takhingga. Beberapa sumber menyertakan persyaratan bahwa kurva mungkin tidak mel...

كونستانتين نوفوسيلوف (بالروسية: Константин Сергеевич Новосёлов)‏    معلومات شخصية الميلاد 23 أغسطس 1974 (50 سنة)[1][2]  نيجني تاجيل  الإقامة سنغافورةنيجني تاجيل (23 أغسطس 1974–1991)دولغوبروندي (1991–1997)تشيرنوغولوفكا (1997–1999)نايميخن (1999–2001)مانشستر (2001–)  مواطنة ال�...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言，清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日（哈薩克蘇維埃社會主義共和國總統） 哈萨克斯坦 哈萨克斯坦政府...

جاك ريتشر: لا عودة مطلقاJack Reacher: Never Go Back (بالإنجليزية) معلومات عامةالصنف الفني حركة، جريمة، إثارةتاريخ الصدور 2016مدة العرض 118 دقيقة اللغة الأصلية الإنجليزيةمأخوذ عن Never Go Back (en) البلد الولايات المتحدةمواقع التصوير Lafayette Square (en) [1] — باتون روج[1] — نيو أورلينز[1] موقع...

For The archaic title for Canada, see Name of Canada. For the New Zealand newspaper, see The Dominion (Wellington). For other uses, see Dominion (disambiguation).This article relies excessively on references to primary sources. Please improve this article by adding secondary or tertiary sources. Find sources: The Dominion Canada – news · newspapers · books · scholar · JSTOR (December 2007) (Learn how and when to remove this message) The DominionTy...

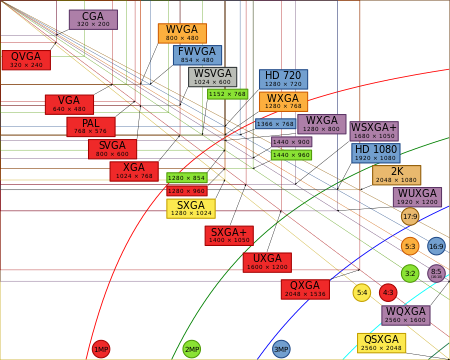
Video of higher resolution than original television For high-definition video in broadcasting, see High-definition television. For other uses, see High definition (disambiguation) and HD (disambiguation). High-definition video (HD video) is video of higher resolution and quality than standard-definition. While there is no standardized meaning for high-definition, generally any video image with considerably more than 480 vertical scan lines (North America) or 576 vertical lines (Europe) is con...

British mathematician Andrew BookerBorn1976NationalityBritishAlma mater University of Virginia Princeton University Scientific careerFieldsMathematicsInstitutionsUniversity of BristolThesis Numerical Tests of Modularity  (2003)Doctoral advisorPeter Sarnak Andrew Richard Booker (born 1976)[1] is a British mathematician who is currently Professor of Pure Mathematics at the University of Bristol.[2] He is an analytic number theorist known for his work on L-functions of ...

أوريسندØresund (بالدنماركية)Öresund (بالسويدية) الموقع الجغرافي / الإداريالإحداثيات 55°45′N 12°45′E / 55.75°N 12.75°E / 55.75; 12.75 جزء من المضائق الدنماركية دول الحوض السويد — الدنمارك هيئة المياهالنوع مضيق مصب الأنهار  القائمة ... Höje River (en) — Kävlinge River (en) — Saxån (en) — Mølleåen (en) — Ni...

Advocacy for exploration and/or colonization of space NASA's artistic poster about the human exploration of Mars: Mars explorers wanted Space advocacy is supporting or advocating human activity in outer space. The advocated purposes range from orbital flight, space exploration, commercialization of space and space settlement, to outright space colonization. There are many different individuals and organizations dedicated to space advocacy. They are usually active in educating the public[1...

Approssimazione della funzione onda quadra attraverso i primi quattro termini della corrispondente trasformata di Fourier In matematica, in particolare in analisi armonica, la serie di Fourier è una rappresentazione di una funzione periodica mediante una combinazione lineare di funzioni sinusoidali. Questo tipo di decomposizione è alla base dell'analisi di Fourier. Indice 1 Storia 2 Definizione 2.1 Forma rettangolare 2.2 Forma complessa 2.3 Forma polare 3 Convergenza delle serie di Fourier ...

グイマツ グイマツの未熟な松かさ 保全状況評価[1] LOWER RISK - Least Concern(IUCN Red List Ver.2.3 (1994))（ダフリアカラマツ Larix gmelinii のカテゴリ） 分類 界 : 植物界 Plantae 門 : 裸子植物門 Pinophyta 綱 : マツ綱 Pinopsida 目 : マツ目 Pinales 科 : マツ科 Pinaceae 属 : カラマツ属 Larix 種 : ダフリアカラマツ L. gmelinii 変種 : グイマツ var. japonica 学名 Larix gmelinii (Rupr.) Kuzen. ver. japonica (Maxi...