Экспонента матрицы
|
Read other articles:

Bantu ethnic group in Namibia OvamboOvambo men in the early 20th centuryTotal population~2 millionRegions with significant populations Namibia~1.3 million (49.5% of Namibia population)[1][2] Angola650,000[2]LanguagesOvambo, English, PortugueseReligionLutheranism, Traditional religion[2]Related ethnic groupsOvimbundu, Herero and other Bantu peoples OvamboPersonOmuwamboPeopleOvamboLanguageOshiwamboCountryOvamboland The Ovambo people (pronounced [ova...

Tenis meja pada Pesta Olahraga Asia 2010LokasiGuangzhou GymnasiumTanggal13 November 2010 (2010-11-13) – 20 November 2010 (2010-11-20)Peserta172 dari 29 negara← 20062014 → Tenis meja pada Pesta Olahraga Asia 2010 adalah cabang olahraga dari Pesta Olahraga Asia 2010 yang diselenggarakan di Guangzhou Gymnasium sejak 13 hingga 20 November 2010.[1] Peraih medali Pertandingan Emas Perak Perunggu Tunggal putradetail Ma Long Tiongkok Wang ...

Census-designated place in Virginia, United StatesChurchvilleCensus-designated placeChurchvilleLocation in the Commonwealth of VirginiaShow map of VirginiaChurchvilleChurchville (the United States)Show map of the United StatesCoordinates: 38°13′34″N 79°09′44″W / 38.22611°N 79.16222°W / 38.22611; -79.16222CountryUnited StatesStateVirginiaCountyAugusta CountyElevation1,424 ft (434 m)Population (2010) • Total194Time zoneUTC−5 (...

Wilayah Operasi ABDAcom American-British-Dutch-Australian (ABDA) Command, nama kode ABDACOM, adalah komando tinggi berumur pendek untuk semua angkatan Sekutu di Asia Tenggara, pada awal tahun 1942, selama Perang Pasifik dalam Perang Dunia II. Tujuan utama komando ini, dipimpin oleh Jenderal Sir Archibald Percival Wavell, adalah memelihara kendali Rintangan Melayu (atau Rintangan Hindia Belanda), sebuah garis khayal yang membentang dari Semenanjung Malaya, melalui Singapura dan pulau paling se...

Irish Sinn Féin politician (born 1958) Pat SheehanMLASheehan in 2023Member of the Legislative Assemblyfor Belfast WestIncumbentAssumed office 7 December 2010Preceded byGerry Adams Personal detailsBorn (1958-05-28) 28 May 1958 (age 65)[1]Belfast, Northern IrelandNationalityIrishPolitical partySinn FéinSpouseSiobhán O'Hanlon (2006; her death)ChildrenCormac SheehanOther organizationsProvisional Irish Republican Army volunteer (formerly) Pat Sheehan (born 28 May 1958) is an Ir...

У этого термина существуют и другие значения, см. Чайки (значения). Чайки Доминиканская чайкаЗападная чайкаКалифорнийская чайкаМорская чайка Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:Вторич...
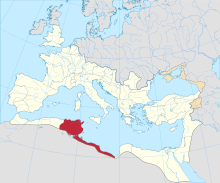
Africa Proconsularis (125 AD) Tagarbala was a Roman–Berber civitas of the province of Byzacena during late antiquity. It was a Roman Catholic diocese. The town is identifiable with stone ruins at Bordj-Tamra,[1] Tamera in modern Tunisia.[2] Roman Tagarbala was also the seat of an ancient Christian episcopal see.[3][4] One bishop is known of this ancient diocese, Fortunatianus, who participated in the synod in Carthage in 484 called by the Vandal king Huneric,...

Approach to restricting system access to authorized users This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the article. (May 2012) In computer systems security, role-based access control (RBAC)[1][2] or role-based security[3] is an approach to restricting system access to authorized users, and to implementing mandatory access control (MAC...

Super Show 2Tur {{{type}}} oleh Super JuniorPoster promosi untuk Super Show 2Sorry, SorryMulai17 Juli 2009 (2009-07-17)Berakhir10 April 2010 (2010-04-10)Putaran7Penampilan3 di Korea Selatan1 di Hong Kong5 di Tiongkok2 di Thailand2 di Taiwan1 di Malaysia1 di Filipinatotal 15Situs websuperjunior.smtown.comKronologi konser Super Junior Super Show (2008–09) Super Show 2 (2009–10) Super Show 3 (2010–11) Super Show 2 tur konser Asia kedua yang dis...

Public middle school and high school in Nabbingo, Wakiso District, UgandaTrinity College NabbingoLocationNabbingo, Wakiso DistrictUgandaCoordinates0°17′28″N 32°28′40″E / 0.29111°N 32.47778°E / 0.29111; 32.47778InformationTypePublic Middle School and High SchoolMottoBe TrueEstablished1942; 82 years ago (1942)Faculty65GenderGirlsNumber of students1,010AthleticsSoccer, cricket, track, netball, volleyball, lawn tennis, table tennis, hockeyWebs...

People of South Asian descent in the U.S. South Asian AmericansTotal population6,268,769[1]1.9% of the total U.S. population (2018)Regions with significant populationsCalifornia · New Jersey · New York · Texas · Massachusetts · Illinois · Florida · Georgia · Maryland · Virginia · Washington · Pennsylvania · NevadaLangua...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (يونيو 2019) الدوري البولندي الممتاز 1930 تفاصيل الموسم الدوري البولندي الممتاز النسخة 10 البلد بولندا المنظم �...

Repulsive force in quantum mechanics In astrophysics and condensed matter physics, electron degeneracy pressure is a quantum mechanical effect critical to understanding the stability of white dwarf stars and metal solids. It is a manifestation of the more general phenomenon of quantum degeneracy pressure. In metals and white dwarf stars, electrons can be modeled as a gas of non-interacting electrons confined to a finite volume. In reality, there are strong electromagnetic forces between the n...

Uni Republik Sosialis Soviet Keanggotaan Perserikatan Bangsa-BangsaKeanggotaanBekas anggota penuhTanggal1945 (1945) – 1991 (1991)Kursi DK PBBPermanenDuta Besar Andrei Gromyko 1946–1948 Yakov Malik 1948–1952 Valerian Zorin 1952–1953 Andrey Vyshinsky 1953–1954 Arkady Sobolev 1955–1960 Valerian Zorin 1960–1963 Nikolai Fedorenko 1963–1968 Yakov Malik 1968–1976 Oleg Troyanovsky 1976–1986 Yuri Dubinin 1986 Alexander Belonogov 1986–1990 Yuli Vorontsov 1990–1991 ...
Progress of miniaturisation, and comparison of sizes of semiconductor manufacturing process nodes with some microscopic objects and visible light wavelengths 1970s The first chips that could be considered microprocessors were designed and manufactured in the late 1960s and early 1970s, including the MP944 used in the F-14 Central Air Data Computer.[1] Intel's 4004 of 1971 is widely regarded as the first commercial microprocessor.[2] Designers predominantly used MOSFET transis...

关于与「中国共产党中央委员会宣传部」標題相近或相同的条目页,請見「中央宣传部」。 中国共产党中央委员会宣传部 加挂牌子 国务院新闻办公室国家新闻出版署(国家版权局)国家电影局 主要领导 部长 李书磊(中央政治局委员、书记处书记兼,副国级) 分管日常工作的副部长 胡和平(正部长级) 副部长(7) 慎海雄(兼中央广电总台台长,正部长级)庄荣...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها...

Concept in classical philosophy For other uses, see Nous (disambiguation). This diagram shows the medieval understanding of spheres of the cosmos, derived from Aristotle, and as per the standard explanation by Ptolemy. It came to be understood that at least the outermost sphere (marked Primũ Mobile) has its own intellect, intelligence or nous – a cosmic equivalent to the human mind. Nous (UK: /naʊs/,[1] US: /nuːs/), from Greek: νοῦς, is a concept from classical philosop...

「IGBT」はこの項目へ転送されています。「LGBT」とは異なります。 この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)出典検索?: 絶縁ゲートバイポーラトランジスタ – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib...

Entity responsible for the creation of the universe Part of a series onTheism Types of faith Agnosticism Apatheism Atheism Classical theism Deism Henotheism Ietsism Ignosticism Monotheism Monism Dualism Monolatry Kathenotheism Omnism Pandeism Panentheism Pantheism Polytheism Transtheism Specific conceptions Brahman Creator Demiurge Deus Father Form of the Good God Great Architect Monad Mother Summum bonum Supreme Being Sustainer The Lord Trinity Tawhid Ditheism Monism Personal Unitarianism In...

























































![{\displaystyle A=\left[{\begin{array}{rrr}2&-1&1\\0&3&-1\\2&1&3\end{array}}\right]~,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5a866884769332fa1a366783b9a1d1955f7dc05)







![{\displaystyle {\begin{aligned}\mathbf {y} _{p}'(t)&=(e^{tA})'\mathbf {z} (t)+e^{tA}\mathbf {z} '(t)\\[6pt]&=Ae^{tA}\mathbf {z} (t)+e^{tA}\mathbf {z} '(t)\\[6pt]&=A\mathbf {y} _{p}(t)+e^{tA}\mathbf {z} '(t)~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ade2a91c46e5fb7cec318107f6f7e4c99a7fe943)

![{\displaystyle {\begin{aligned}e^{tA}\mathbf {z} '(t)&=\mathbf {b} (t)\\[6pt]\mathbf {z} '(t)&=(e^{tA})^{-1}\mathbf {b} (t)\\[6pt]\mathbf {z} (t)&=\int _{0}^{t}e^{-uA}\mathbf {b} (u)\,du+\mathbf {c} ~.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28f09b0f45bee4e56ae6c7ecc9200f3d2b5d6953)

