–§—ГћБ–љ–Ї—Ж–Є–Є –С–µћБ—Б—Б–µ–ї—П –≤ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–µ вАФ —Б–µ–Љ–µ–є—Б—В–≤–Њ —Д—Г–љ–Ї—Ж–Є–є , —П–≤–ї—П—О—Й–Є—Е—Б—П –Ї–∞–љ–Њ–љ–Є—З–µ—Б–Ї–Є–Љ–Є —А–µ—И–µ–љ–Є—П–Љ–Є –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П –С–µ—Б—Б–µ–ї—П:
x
2
d
2
y
d
x
2
+
x
d
y
d
x
+
(
x
2
− вИТ -->
α ќ± -->
2
)
y
=
0
,
{\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+x{\frac {dy}{dx}}+(x^{2}-\alpha ^{2})y=0,}
–≥–і–µ
α ќ± -->
{\displaystyle \alpha }
–≤–µ—Й–µ—Б—В–≤–µ–љ–љ–Њ–µ —З–Є—Б–ї–Њ (–≤ –Њ–±—Й–µ–Љ —Б–ї—Г—З–∞–µ –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Њ–µ), –љ–∞–Ј—Л–≤–∞–µ–Љ–Њ–µ –њ–Њ—А—П–і–Ї–Њ–Љ .
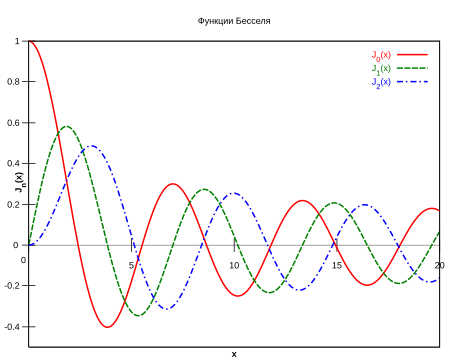
–У—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–є –С–µ—Б—Б–µ–ї—П –њ–µ—А–≤–Њ–≥–Њ —А–Њ–і–∞ –Э–∞–Є–±–Њ–ї–µ–µ —З–∞—Б—В–Њ –Є—Б–њ–Њ–ї—М–Ј—Г–µ–Љ—Л–µ —Д—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П вАФ —Д—Г–љ–Ї—Ж–Є–Є —Ж–µ–ї—Л—Е –њ–Њ—А—П–і–Ї–Њ–≤.
–•–Њ—В—П
α ќ± -->
{\displaystyle \alpha }
(
− вИТ -->
α ќ± -->
)
{\displaystyle (-\alpha )}
–≥–ї–∞–і–Ї–Њ–є –њ–Њ
α ќ± -->
{\displaystyle \alpha }
–§—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П –≤–њ–µ—А–≤—Л–µ –±—Л–ї–Є –Њ–њ—А–µ–і–µ–ї–µ–љ—Л —И–≤–µ–є—Ж–∞—А—Б–Ї–Є–Љ –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Њ–Љ –Ф–∞–љ–Є–Є–ї–Њ–Љ –С–µ—А–љ—Г–ї–ї–Є , –∞ –љ–∞–Ј–≤–∞–љ—Л –≤ —З–µ—Б—В—М –§—А–Є–і—А–Є—Е–∞ –С–µ—Б—Б–µ–ї—П .
–£—А–∞–≤–љ–µ–љ–Є–µ –С–µ—Б—Б–µ–ї—П –≤–Њ–Ј–љ–Є–Ї–∞–µ—В –≤–Њ –≤—А–µ–Љ—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П —А–µ—И–µ–љ–Є–є —Г—А–∞–≤–љ–µ–љ–Є—П –Ы–∞–њ–ї–∞—Б–∞ –Є —Г—А–∞–≤–љ–µ–љ–Є—П –У–µ–ї—М–Љ–≥–Њ–ї—М—Ж–∞ –≤ —Ж–Є–ї–Є–љ–і—А–Є—З–µ—Б–Ї–Є—Е –Є —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е. –Я–Њ—Н—В–Њ–Љ—Г —Д—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П –њ—А–Є–Љ–µ–љ—П—О—В—Б—П –њ—А–Є —А–µ—И–µ–љ–Є–Є –Љ–љ–Њ–≥–Є—Е –Ј–∞–і–∞—З –Њ —А–∞—Б–њ—А–Њ—Б—В—А–∞–љ–µ–љ–Є–Є –≤–Њ–ї–љ, —Б—В–∞—В–Є—З–µ—Б–Ї–Є—Е –њ–Њ—В–µ–љ—Ж–Є–∞–ї–∞—Е –Є —В. –њ., –љ–∞–њ—А–Є–Љ–µ—А:
—Н–ї–µ–Ї—В—А–Њ–Љ–∞–≥–љ–Є—В–љ—Л–µ –≤–Њ–ї–љ—Л –≤ —Ж–Є–ї–Є–љ–і—А–Є—З–µ—Б–Ї–Њ–Љ –≤–Њ–ї–љ–Њ–≤–Њ–і–µ ;—В–µ–њ–ї–Њ–њ—А–Њ–≤–Њ–і–љ–Њ—Б—В—М –≤ —Ж–Є–ї–Є–љ–і—А–Є—З–µ—Б–Ї–Є—Е –Њ–±—К–µ–Ї—В–∞—Е;—Д–Њ—А–Љ—Л –Ї–Њ–ї–µ–±–∞–љ–Є—П —В–Њ–љ–Ї–Њ–є –Ї—А—Г–≥–ї–Њ–є –Љ–µ–Љ–±—А–∞–љ—Л;
—А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–Є–µ –Є–љ—В–µ–љ—Б–Є–≤–љ–Њ—Б—В–Є —Б–≤–µ—В–∞, –і–Є—Д—А–∞–≥–Є—А–Њ–≤–∞–љ–љ–Њ–≥–Њ –љ–∞ –Ї—А—Г–≥–ї–Њ–Љ –Њ—В–≤–µ—А—Б—В–Є–Є;
—Б–Ї–Њ—А–Њ—Б—В—М —З–∞—Б—В–Є—Ж –≤ —Ж–Є–ї–Є–љ–і—А–µ, –Ј–∞–њ–Њ–ї–љ–µ–љ–љ–Њ–Љ –ґ–Є–і–Ї–Њ—Б—В—М—О –Є –≤—А–∞—Й–∞—О—Й–µ–Љ—Б—П –≤–Њ–Ї—А—Г–≥ —Б–≤–Њ–µ–є –Њ—Б–Є;
–≤–Њ–ї–љ–Њ–≤—Л–µ —Д—Г–љ–Ї—Ж–Є–Є –≤ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є —Б–Є–Љ–Љ–µ—В—А–Є—З–љ–Њ–Љ –њ–Њ—В–µ–љ—Ж–Є–∞–ї—М–љ–Њ–Љ —П—Й–Є–Ї–µ. –§—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П –њ—А–Є–Љ–µ–љ—П—О—В—Б—П –Є –≤ —А–µ—И–µ–љ–Є–Є –і—А—Г–≥–Є—Е –Ј–∞–і–∞—З, –љ–∞–њ—А–Є–Љ–µ—А, –њ—А–Є –Њ–±—А–∞–±–Њ—В–Ї–µ —Б–Є–≥–љ–∞–ї–Њ–≤.
–§—Г–љ–Ї—Ж–Є—П –С–µ—Б—Б–µ–ї—П —П–≤–ї—П–µ—В—Б—П –Њ–±–Њ–±—Й–µ–љ–Є–µ–Љ —Д—Г–љ–Ї—Ж–Є–Є —Б–Є–љ—Г—Б–∞. –Х–µ –Љ–Њ–ґ–љ–Њ —В—А–∞–Ї—В–Њ–≤–∞—В—М –Ї–∞–Ї –Ї–Њ–ї–µ–±–∞–љ–Є–µ —Б—В—А—Г–љ—Л —Б –њ–µ—А–µ–Љ–µ–љ–љ–Њ–є —В–Њ–ї—Й–Є–љ–Њ–є, –њ–µ—А–µ–Љ–µ–љ–љ—Л–Љ –љ–∞—В—П–ґ–µ–љ–Є–µ–Љ (–Є–ї–Є –Њ–і–љ–Њ–≤—А–µ–Љ–µ–љ–љ–Њ –Њ–±–Њ–Є–Љ–Є —Г—Б–ї–Њ–≤–Є—П–Љ–Є); –Ї–Њ–ї–µ–±–∞–љ–Є—П–Љ–Є –≤ —Б—А–µ–і–µ —Б –њ–µ—А–µ–Љ–µ–љ–љ—Л–Љ–Є —Б–≤–Њ–є—Б—В–≤–∞–Љ–Є; –Ї–Њ–ї–µ–±–∞–љ–Є—П–Љ–Є –і–Є—Б–Ї–Њ–≤–Њ–є –Љ–µ–Љ–±—А–∞–љ—Л –Є —В. –і.
–Я–Њ—Б–Ї–Њ–ї—М–Ї—Г –њ—А–Є–≤–µ–і—С–љ–љ–Њ–µ —Г—А–∞–≤–љ–µ–љ–Є–µ —П–≤–ї—П–µ—В—Б—П –ї–Є–љ–µ–є–љ—Л–Љ –і–Є—Д—Д–µ—А–µ–љ—Ж–Є–∞–ї—М–љ—Л–Љ —Г—А–∞–≤–љ–µ–љ–Є–µ–Љ –≤—В–Њ—А–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞, —Г –љ–µ–≥–Њ –і–Њ–ї–ґ–љ–Њ –±—Л—В—М –і–≤–∞ –ї–Є–љ–µ–є–љ–Њ –љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л—Е —А–µ—И–µ–љ–Є—П. –Ю–і–љ–∞–Ї–Њ –≤ –Ј–∞–≤–Є—Б–Є–Љ–Њ—Б—В–Є –Њ—В –Њ–±—Б—В–Њ—П—В–µ–ї—М—Б—В–≤ –≤—Л–±–Є—А–∞—О—В—Б—П —А–∞–Ј–љ—Л–µ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є—П —Н—В–Є—Е —А–µ—И–µ–љ–Є–є. –Э–Є–ґ–µ –њ—А–Є–≤–µ–і–µ–љ—Л –љ–µ–Ї–Њ—В–Њ—А—Л–µ –Є–Ј –љ–Є—Е.
–§—Г–љ–Ї—Ж–Є—П–Љ–Є –С–µ—Б—Б–µ–ї—П –њ–µ—А–≤–Њ–≥–Њ —А–Њ–і–∞, –Њ–±–Њ–Ј–љ–∞—З–∞–µ–Љ—Л–Љ–Є
J
α ќ± -->
(
x
)
{\displaystyle J_{\alpha }(x)}
x
=
0
{\displaystyle x=0}
α ќ± -->
{\displaystyle \alpha }
—А—П–і –Ґ–µ–є–ї–Њ—А–∞ –Њ–Ї–Њ–ї–Њ –љ—Г–ї—П (–Є–ї–Є –≤ –±–Њ–ї–µ–µ –Њ–±—Й–Є–є —Б—В–µ–њ–µ–љ–љ–Њ–є —А—П–і –њ—А–Є –љ–µ—Ж–µ–ї—Л—Е
α ќ± -->
{\displaystyle \alpha }
J
α ќ± -->
(
x
)
=
∑ вИС -->
m
=
0
∞ вИЮ -->
(
− вИТ -->
1
)
m
m
!
Γ ќУ -->
(
m
+
α ќ± -->
+
1
)
(
x
2
)
2
m
+
α ќ± -->
.
{\displaystyle J_{\alpha }(x)=\sum _{m=0}^{\infty }{\frac {(-1)^{m}}{m!\,\Gamma (m+\alpha +1)}}{\left({\frac {x}{2}}\right)}^{2m+\alpha }.}
–Ч–і–µ—Б—М
Γ ќУ -->
(
z
)
{\displaystyle \Gamma (z)}
–≥–∞–Љ–Љ–∞-—Д—Г–љ–Ї—Ж–Є—П –≠–є–ї–µ—А–∞ , –Њ–±–Њ–±—Й–µ–љ–Є–µ —Д–∞–Ї—В–Њ—А–Є–∞–ї–∞ –љ–∞ –љ–µ—Ж–µ–ї—Л–µ –Ј–љ–∞—З–µ–љ–Є—П. –У—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П –њ–Њ—Е–Њ–ґ –љ–∞ —Б–Є–љ—Г—Б–Њ–Є–і—Г , –Ї–Њ–ї–µ–±–∞–љ–Є—П –Ї–Њ—В–Њ—А–Њ–є –Ј–∞—В—Г—Е–∞—О—В –њ—А–Њ–њ–Њ—А—Ж–Є–Њ–љ–∞–ї—М–љ–Њ
1
x
{\displaystyle {\frac {1}{\sqrt {x}}}}
–љ—Г–ї–Є —Д—Г–љ–Ї—Ж–Є–Є —А–∞—Б–њ–Њ–ї–Њ–ґ–µ–љ—Л –љ–µ –њ–µ—А–Є–Њ–і–Є—З–љ–Њ (–Њ–і–љ–∞–Ї–Њ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Љ–µ–ґ–і—Г –і–≤—Г–Љ—П –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ—Л–Љ–Є –љ—Г–ї—П–Љ–Є —Б—В—А–µ–Љ–Є—В—Б—П –Ї
π ѕА -->
{\displaystyle \pi }
x
→ вЖТ -->
∞ вИЮ -->
{\displaystyle x\to \infty }
[ 1]
–Э–Є–ґ–µ –њ—А–Є–≤–µ–і–µ–љ—Л –≥—А–∞—Д–Є–Ї–Є
J
α ќ± -->
(
x
)
{\displaystyle J_{\alpha }(x)}
α ќ± -->
=
0
,
1
,
2
{\displaystyle \alpha =0,1,2}
–У—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П –њ–µ—А–≤–Њ–≥–Њ —А–Њ–і–∞ J –Х—Б–ї–Є
α ќ± -->
{\displaystyle \alpha }
J
α ќ± -->
(
x
)
{\displaystyle J_{\alpha }(x)}
J
− вИТ -->
α ќ± -->
(
x
)
{\displaystyle J_{-\alpha }(x)}
α ќ± -->
{\displaystyle \alpha }
J
− вИТ -->
α ќ± -->
(
x
)
=
(
− вИТ -->
1
)
α ќ± -->
J
α ќ± -->
(
x
)
.
{\displaystyle J_{-\alpha }(x)=(-1)^{\alpha }J_{\alpha }(x).}
–Ю–љ–Њ –Њ–Ј–љ–∞—З–∞–µ—В, —З—В–Њ –≤ —Н—В–Њ–Љ —Б–ї—Г—З–∞–µ —Д—Г–љ–Ї—Ж–Є–Є –ї–Є–љ–µ–є–љ–Њ –Ј–∞–≤–Є—Б–Є–Љ—Л. –Ґ–Њ–≥–і–∞ –≤—В–Њ—А—Л–Љ —А–µ—И–µ–љ–Є–µ–Љ —Г—А–∞–≤–љ–µ–љ–Є—П —Б—В–∞–љ–µ—В —Д—Г–љ–Ї—Ж–Є—П –С–µ—Б—Б–µ–ї—П –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞ (—Б–Љ. –љ–Є–ґ–µ).
–Ь–Њ–ґ–љ–Њ –і–∞—В—М –і—А—Г–≥–Њ–µ –Њ–њ—А–µ–і–µ–ї–µ–љ–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П –і–ї—П —Ж–µ–ї—Л—Е –Ј–љ–∞—З–µ–љ–Є–є
α ќ± -->
{\displaystyle \alpha }
J
α ќ± -->
(
x
)
=
1
π ѕА -->
∫ вИЂ -->
0
π ѕА -->
cos
вБ° -->
(
α ќ± -->
τ ѕД -->
− вИТ -->
x
sin
вБ° -->
τ ѕД -->
)
d
τ ѕД -->
.
{\displaystyle J_{\alpha }(x)={\frac {1}{\pi }}\int \limits _{0}^{\pi }\!\cos(\alpha \tau -x\sin \tau )\,d\tau .}
–≠—В–Њ—В –њ–Њ–і—Е–Њ–і –Є—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–ї –С–µ—Б—Б–µ–ї—М, –Є–Ј—Г—З–Є–≤ —Б –µ–≥–Њ –њ–Њ–Љ–Њ—Й—М—О –љ–µ–Ї–Њ—В–Њ—А—Л–µ —Б–≤–Њ–є—Б—В–≤–∞ —Д—Г–љ–Ї—Ж–Є–є. –Т–Њ–Ј–Љ–Њ–ґ–љ–Њ –Є –і—А—Г–≥–Њ–µ –Є–љ—В–µ–≥—А–∞–ї—М–љ–Њ–µ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ:
J
α ќ± -->
(
x
)
=
1
2
π ѕА -->
∫ вИЂ -->
− вИТ -->
π ѕА -->
π ѕА -->
e
i
(
α ќ± -->
τ ѕД -->
− вИТ -->
x
sin
вБ° -->
τ ѕД -->
)
d
τ ѕД -->
.
{\displaystyle J_{\alpha }(x)={\frac {1}{2\pi }}\int \limits _{-\pi }^{\pi }\!e^{i(\alpha \tau -x\sin \tau )}\,d\tau .}
[ 2] –Ф–ї—П –љ–∞—Е–Њ–ґ–і–µ–љ–Є—П –Є–љ—В–µ–≥—А–∞–ї—М–љ–Њ–≥–Њ –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є—П —Д—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П –≤ —Б–ї—Г—З–∞–µ –љ–µ—Ж–µ–ї—Л—Е
α ќ± -->
{\displaystyle \alpha }
2
π ѕА -->
{\displaystyle 2\pi }
− вИТ -->
∞ вИЮ -->
{\displaystyle -\infty }
1
{\displaystyle 1}
φ ѕЖ -->
=
− вИТ -->
π ѕА -->
{\textstyle \varphi =-\pi }
1
{\displaystyle 1}
+
∞ вИЮ -->
{\displaystyle +\infty }
φ ѕЖ -->
=
π ѕА -->
{\textstyle \varphi =\pi }
J
α ќ± -->
(
x
)
=
1
2
π ѕА -->
∫ вИЂ -->
− вИТ -->
π ѕА -->
π ѕА -->
e
i
(
x
sin
вБ° -->
(
φ ѕЖ -->
)
− вИТ -->
α ќ± -->
φ ѕЖ -->
)
d
φ ѕЖ -->
− вИТ -->
sin
вБ° -->
(
α ќ± -->
π ѕА -->
)
π ѕА -->
∫ вИЂ -->
1
∞ вИЮ -->
e
− вИТ -->
1
2
x
(
r
− вИТ -->
1
r
)
r
α ќ± -->
+
1
d
r
.
{\displaystyle J_{\alpha }(x)={\frac {1}{2\pi }}\int \limits _{-\pi }^{\pi }\!e^{i(x\sin(\varphi )-\alpha \varphi )}d\varphi -{\frac {\sin(\alpha \pi )}{\pi }}\int \limits _{1}^{\infty }{\frac {e^{-{\frac {1}{2}}x(r-{\frac {1}{r}})}}{{}r^{\alpha +1}}}dr.}
–Э–µ—В—А—Г–і–љ–Њ —Г–±–µ–і–Є—В—М—Б—П, —З—В–Њ –њ—А–Є —Ж–µ–ї—Л—Е
α ќ± -->
{\displaystyle \alpha }
–§—Г–љ–Ї—Ж–Є–Є –Э–µ–є–Љ–∞–љ–∞ вАФ —А–µ—И–µ–љ–Є—П
Y
α ќ± -->
(
x
)
{\displaystyle Y_{\alpha }(x)}
x
=
0
{\displaystyle x=0}
–≠—В–∞ —Д—Г–љ–Ї—Ж–Є—П —Б–≤—П–Ј–∞–љ–∞ —Б
J
α ќ± -->
(
x
)
{\displaystyle J_{\alpha }(x)}
Y
α ќ± -->
(
x
)
=
J
α ќ± -->
(
x
)
cos
вБ° -->
(
α ќ± -->
π ѕА -->
)
− вИТ -->
J
− вИТ -->
α ќ± -->
(
x
)
sin
вБ° -->
(
α ќ± -->
π ѕА -->
)
,
{\displaystyle Y_{\alpha }(x)={\frac {J_{\alpha }(x)\cos(\alpha \pi )-J_{-\alpha }(x)}{\sin(\alpha \pi )}},}
–≥–і–µ –≤ —Б–ї—Г—З–∞–µ —Ж–µ–ї–Њ–≥–Њ
α ќ± -->
{\displaystyle \alpha }
–њ—А–µ–і–µ–ї –њ–Њ
α ќ± -->
{\displaystyle \alpha }
–њ—А–∞–≤–Є–ї–∞ –Ы–Њ–њ–Є—В–∞–ї—П .
–§—Г–љ–Ї—Ж–Є–Є –Э–µ–є–Љ–∞–љ–∞ —В–∞–Ї–ґ–µ –љ–∞–Ј—Л–≤–∞—О—В—Б—П —Д—Г–љ–Ї—Ж–Є—П–Љ–Є –С–µ—Б—Б–µ–ї—П –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞. –Ы–Є–љ–µ–є–љ–∞—П –Ї–Њ–Љ–±–Є–љ–∞—Ж–Є—П —Д—Г–љ–Ї—Ж–Є–є –С–µ—Б—Б–µ–ї—П –њ–µ—А–≤–Њ–≥–Њ –Є –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–Њ–≤ —П–≤–ї—П–µ—В —Б–Њ–±–Њ–є –њ–Њ–ї–љ–Њ–µ —А–µ—И–µ–љ–Є–µ —Г—А–∞–≤–љ–µ–љ–Є—П –С–µ—Б—Б–µ–ї—П:
y
(
x
)
=
C
1
J
α ќ± -->
(
x
)
+
C
2
Y
α ќ± -->
(
x
)
.
{\displaystyle y(x)=C_{1}J_{\alpha }(x)+C_{2}Y_{\alpha }(x).}
–Э–Є–ґ–µ –њ—А–Є–≤–µ–і—С–љ –≥—А–∞—Д–Є–Ї
Y
α ќ± -->
(
x
)
{\displaystyle Y_{\alpha }(x)}
α ќ± -->
=
0
,
1
,
2
{\displaystyle \alpha =0,1,2}
–У—А–∞—Д–Є–Ї —Д—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞ N –Т —А—П–і–µ –Ї–љ–Є–≥ —Д—Г–љ–Ї—Ж–Є–Є –Э–µ–є–Љ–∞–љ–∞ –Њ–±–Њ–Ј–љ–∞—З–∞—О—В—Б—П
N
α ќ± -->
(
x
)
{\displaystyle N_{\alpha }(x)}
–°—Д–µ—А–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П –њ–µ—А–≤–Њ–≥–Њ —А–Њ–і–∞, jn (x )n = 0, 1, 2 –°—Д–µ—А–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞, yn (x )n = 0, 1, 2 –Я—А–Є —А–µ—И–µ–љ–Є–Є —Г—А–∞–≤–љ–µ–љ–Є—П –У–µ–ї—М–Љ–≥–Њ–ї—М—Ж–∞ –≤ —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е –Ї–Њ–Њ—А–і–Є–љ–∞—В–∞—Е –Љ–µ—В–Њ–і–Њ–Љ —А–∞–Ј–і–µ–ї–µ–љ–Є—П –њ–µ—А–µ–Љ–µ–љ–љ—Л—Е —Г—А–∞–≤–љ–µ–љ–Є–µ –љ–∞ —А–∞–і–Є–∞–ї—М–љ—Г—О —З–∞—Б—В—М –Є–Љ–µ–µ—В –≤–Є–і
x
2
d
2
y
d
x
2
+
2
x
d
y
d
x
+
(
x
2
− вИТ -->
n
(
n
+
1
)
)
y
=
0.
{\displaystyle x^{2}{\frac {d^{2}y}{dx^{2}}}+2x{\frac {dy}{dx}}+\left(x^{2}-n(n+1)\right)y=0.}
–Ф–≤–∞ –ї–Є–љ–µ–є–љ–Њ-–љ–µ–Ј–∞–≤–Є—Б–Є–Љ—Л—Е —А–µ—И–µ–љ–Є—П –љ–∞–Ј—Л–≤–∞—О—В—Б—П —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–Љ–Є —Д—Г–љ–Ї—Ж–Є—П–Љ–Є –С–µ—Б—Б–µ–ї—П jn –Є yn , –Є —Б–≤—П–Ј–∞–љ—Л —Б –Њ–±—Л—З–љ—Л–Љ–Є —Д—Г–љ–Ї—Ж–Є—П–Љ–Є –С–µ—Б—Б–µ–ї—П Jn –Є –Э–µ–є–Љ–∞–љ–∞ Yn —Б –њ–Њ–Љ–Њ—Й—М—О[ 3]
j
n
(
x
)
=
π ѕА -->
2
x
J
n
+
1
2
(
x
)
,
y
n
(
x
)
=
π ѕА -->
2
x
Y
n
+
1
2
(
x
)
=
(
− вИТ -->
1
)
n
+
1
π ѕА -->
2
x
J
− вИТ -->
n
− вИТ -->
1
2
(
x
)
.
{\displaystyle {\begin{aligned}j_{n}(x)&={\sqrt {\frac {\pi }{2x}}}J_{n+{\frac {1}{2}}}(x),\\y_{n}(x)&={\sqrt {\frac {\pi }{2x}}}Y_{n+{\frac {1}{2}}}(x)=(-1)^{n+1}{\sqrt {\frac {\pi }{2x}}}J_{-n-{\frac {1}{2}}}(x).\end{aligned}}}
yn —В–∞–Ї–ґ–µ –Њ–±–Њ–Ј–љ–∞—З–∞–µ—В—Б—П nn –Є–ї–Є ќЈn ; –љ–µ–Ї–Њ—В–Њ—А—Л–µ –∞–≤—В–Њ—А—Л –љ–∞–Ј—Л–≤–∞—О—В —Н—В–Є —Д—Г–љ–Ї—Ж–Є–Є —Б—Д–µ—А–Є—З–µ—Б–Ї–Є–Љ–Є —Д—Г–љ–Ї—Ж–Є—П–Љ–Є –Э–µ–є–Љ–∞–љ–∞ .
–°—Д–µ—А–Є—З–µ—Б–Ї–Є–µ —Д—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П —В–∞–Ї–ґ–µ –Љ–Њ–≥—Г—В –±—Л—В—М –Ј–∞–њ–Є—Б–∞–љ—Л –Ї–∞–Ї (—Д–Њ—А–Љ—Г–ї–∞ –†–µ–ї–µ—П )[ 4]
j
n
(
x
)
=
(
− вИТ -->
x
)
n
(
1
x
d
d
x
)
n
sin
вБ° -->
x
x
,
y
n
(
x
)
=
− вИТ -->
(
− вИТ -->
x
)
n
(
1
x
d
d
x
)
n
cos
вБ° -->
x
x
.
{\displaystyle {\begin{aligned}j_{n}(x)&=(-x)^{n}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{n}{\frac {\sin x}{x}},\\y_{n}(x)&=-(-x)^{n}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{n}{\frac {\cos x}{x}}.\end{aligned}}}
–Э–µ—Б–Ї–Њ–ї—М–Ї–Њ –њ–µ—А–≤—Л—Е —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є –С–µ—Б—Б–µ–ї—П[ 5]
j
0
(
x
)
=
sin
вБ° -->
x
x
,
j
1
(
x
)
=
sin
вБ° -->
x
x
2
− вИТ -->
cos
вБ° -->
x
x
,
j
2
(
x
)
=
(
3
x
2
− вИТ -->
1
)
sin
вБ° -->
x
x
− вИТ -->
3
cos
вБ° -->
x
x
2
,
j
3
(
x
)
=
(
15
x
3
− вИТ -->
6
x
)
sin
вБ° -->
x
x
− вИТ -->
(
15
x
2
− вИТ -->
1
)
cos
вБ° -->
x
x
{\displaystyle {\begin{aligned}j_{0}(x)&={\frac {\sin x}{x}},\\j_{1}(x)&={\frac {\sin x}{x^{2}}}-{\frac {\cos x}{x}},\\j_{2}(x)&=\left({\frac {3}{x^{2}}}-1\right){\frac {\sin x}{x}}-{\frac {3\cos x}{x^{2}}},\\j_{3}(x)&=\left({\frac {15}{x^{3}}}-{\frac {6}{x}}\right){\frac {\sin x}{x}}-\left({\frac {15}{x^{2}}}-1\right){\frac {\cos x}{x}}\end{aligned}}}
–Є –Э–µ–є–Љ–∞–љ–∞[ 6]
y
0
(
x
)
=
− вИТ -->
j
− вИТ -->
1
(
x
)
=
− вИТ -->
cos
вБ° -->
x
x
,
y
1
(
x
)
=
j
− вИТ -->
2
(
x
)
=
− вИТ -->
cos
вБ° -->
x
x
2
− вИТ -->
sin
вБ° -->
x
x
,
y
2
(
x
)
=
− вИТ -->
j
− вИТ -->
3
(
x
)
=
(
− вИТ -->
3
x
2
+
1
)
cos
вБ° -->
x
x
− вИТ -->
3
sin
вБ° -->
x
x
2
,
y
3
(
x
)
=
j
− вИТ -->
4
(
x
)
=
(
− вИТ -->
15
x
3
+
6
x
)
cos
вБ° -->
x
x
− вИТ -->
(
15
x
2
− вИТ -->
1
)
sin
вБ° -->
x
x
.
{\displaystyle {\begin{aligned}y_{0}(x)&=-j_{-1}(x)=-{\frac {\cos x}{x}},\\y_{1}(x)&=j_{-2}(x)=-{\frac {\cos x}{x^{2}}}-{\frac {\sin x}{x}},\\y_{2}(x)&=-j_{-3}(x)=\left(-{\frac {3}{x^{2}}}+1\right){\frac {\cos x}{x}}-{\frac {3\sin x}{x^{2}}},\\y_{3}(x)&=j_{-4}(x)=\left(-{\frac {15}{x^{3}}}+{\frac {6}{x}}\right){\frac {\cos x}{x}}-\left({\frac {15}{x^{2}}}-1\right){\frac {\sin x}{x}}.\end{aligned}}}
–Я—А–Њ–Є–Ј–≤–Њ–і—П—Й–Є–µ —Д—Г–љ–Ї—Ж–Є–Є —Б—Д–µ—А–Є—З–µ—Б–Ї–Є—Е —Д—Г–љ–Ї—Ж–Є–є –С–µ—Б—Б–µ–ї—П[ 7]
1
z
cos
вБ° -->
(
z
2
− вИТ -->
2
z
t
)
=
∑ вИС -->
n
=
0
∞ вИЮ -->
t
n
n
!
j
n
− вИТ -->
1
(
z
)
,
1
z
sin
вБ° -->
(
z
2
− вИТ -->
2
z
t
)
=
∑ вИС -->
n
=
0
∞ вИЮ -->
t
n
n
!
y
n
− вИТ -->
1
(
z
)
.
{\displaystyle {\begin{aligned}{\frac {1}{z}}\cos \left({\sqrt {z^{2}-2zt}}\right)&=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}j_{n-1}(z),\\{\frac {1}{z}}\sin \left({\sqrt {z^{2}-2zt}}\right)&=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}y_{n-1}(z).\end{aligned}}}
–Т —Б–ї–µ–і—Г—О—Й–Є—Е —Д–Њ—А–Љ—Г–ї–∞—Е fn –Љ–Њ–ґ–µ—В –±—Л—В—М –Ј–∞–Љ–µ–љ–µ–љ–Њ –љ–∞ jn , yn , h (1)n h (2)n h (1)n h (2)n n = 0, ¬±1, ¬±2, ...[ 8]
(
1
z
d
d
z
)
m
(
z
n
+
1
f
n
(
z
)
)
=
z
n
− вИТ -->
m
+
1
f
n
− вИТ -->
m
(
z
)
,
(
1
z
d
d
z
)
m
(
z
− вИТ -->
n
f
n
(
z
)
)
=
(
− вИТ -->
1
)
m
z
− вИТ -->
n
− вИТ -->
m
f
n
+
m
(
z
)
.
{\displaystyle {\begin{aligned}\left({\frac {1}{z}}{\frac {d}{dz}}\right)^{m}\left(z^{n+1}f_{n}(z)\right)&=z^{n-m+1}f_{n-m}(z),\\\left({\frac {1}{z}}{\frac {d}{dz}}\right)^{m}\left(z^{-n}f_{n}(z)\right)&=(-1)^{m}z^{-n-m}f_{n+m}(z).\end{aligned}}}
–Я—Г—Б—В—М
μ ќЉ -->
1
,
μ ќЉ -->
2
{\displaystyle \mu _{1},\mu _{2}}
J
α ќ± -->
(
x
)
{\displaystyle J_{\alpha }(x)}
[ 1]
∫ вИЂ -->
0
1
x
J
α ќ± -->
(
μ ќЉ -->
1
x
)
J
α ќ± -->
(
μ ќЉ -->
2
x
)
d
x
=
{
0
;
μ ќЉ -->
1
≠ вЙ† -->
μ ќЉ -->
2
1
2
(
J
α ќ± -->
′
(
μ ќЉ -->
1
)
)
2
;
μ ќЉ -->
1
=
μ ќЉ -->
2
{\displaystyle \int _{0}^{1}{xJ_{\alpha }(\mu _{1}x)J_{\alpha }(\mu _{2}x)dx}=\left\{{\begin{matrix}0&{\mbox{;}}\quad \mu _{1}\neq \mu _{2}\\\\{\frac {1}{2}}(J'_{\alpha }(\mu _{1}))^{2}&{\mbox{;}}\quad \mu _{1}=\mu _{2}\end{matrix}}\right.}
–Ф–ї—П —Д—Г–љ–Ї—Ж–Є–є –С–µ—Б—Б–µ–ї—П –њ–µ—А–≤–Њ–≥–Њ –Є –≤—В–Њ—А–Њ–≥–Њ —А–Њ–і–∞ –Є–Ј–≤–µ—Б—В–љ—Л –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Є–µ —Д–Њ—А–Љ—Г–ї—Л. –Я—А–Є –Љ–∞–ї—Л—Е –∞—А–≥—Г–Љ–µ–љ—В–∞—Е
(
0
<
x
≪ вЙ™ -->
α ќ± -->
+
1
)
{\displaystyle (0<x\ll {\sqrt {\alpha +1}})}
α ќ± -->
{\displaystyle \alpha }
[ 9]
J
α ќ± -->
(
x
)
→ вЖТ -->
1
Γ ќУ -->
(
α ќ± -->
+
1
)
(
x
2
)
α ќ± -->
,
{\displaystyle J_{\alpha }(x)\rightarrow {\frac {1}{\Gamma (\alpha +1)}}\left({\frac {x}{2}}\right)^{\alpha },}
Y
α ќ± -->
(
x
)
→ вЖТ -->
{
2
π ѕА -->
[
ln
вБ° -->
(
x
/
2
)
+
γ ќ≥ -->
]
;
α ќ± -->
=
0
− вИТ -->
Γ ќУ -->
(
α ќ± -->
)
π ѕА -->
(
2
x
)
α ќ± -->
;
α ќ± -->
>
0
{\displaystyle Y_{\alpha }(x)\rightarrow \left\{{\begin{matrix}{\frac {2}{\pi }}\left[\ln(x/2)+\gamma \right]&{\mbox{;}}\quad \alpha =0\\\\-{\frac {\Gamma (\alpha )}{\pi }}\left({\frac {2}{x}}\right)^{\alpha }&{\mbox{;}}\quad \alpha >0\end{matrix}}\right.}
–≥–і–µ
γ ќ≥ -->
{\displaystyle \gamma }
–њ–Њ—Б—В–Њ—П–љ–љ–∞—П –≠–є–ї–µ—А–∞ вАФ –Ь–∞—Б–Ї–µ—А–Њ–љ–Є (0,5772вА¶), –∞
Γ ќУ -->
{\displaystyle \Gamma }
–≥–∞–Љ–Љ–∞-—Д—Г–љ–Ї—Ж–Є—П –≠–є–ї–µ—А–∞ . –Ф–ї—П –±–Њ–ї—М—И–Є—Е –∞—А–≥—Г–Љ–µ–љ—В–Њ–≤ (
x
≫ вЙЂ -->
|
α ќ± -->
2
− вИТ -->
1
/
4
|
{\displaystyle x\gg |\alpha ^{2}-1/4|}
J
α ќ± -->
(
x
)
→ вЖТ -->
2
π ѕА -->
x
cos
вБ° -->
(
x
− вИТ -->
α ќ± -->
π ѕА -->
2
− вИТ -->
π ѕА -->
4
)
,
{\displaystyle J_{\alpha }(x)\rightarrow {\sqrt {\frac {2}{\pi x}}}\cos \left(x-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right),}
Y
α ќ± -->
(
x
)
→ вЖТ -->
2
π ѕА -->
x
sin
вБ° -->
(
x
− вИТ -->
α ќ± -->
π ѕА -->
2
− вИТ -->
π ѕА -->
4
)
.
{\displaystyle Y_{\alpha }(x)\rightarrow {\sqrt {\frac {2}{\pi x}}}\sin \left(x-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right).}
–Ш—Б–њ–Њ–ї—М–Ј–Њ–≤–∞–љ–Є–µ —Б–ї–µ–і—Г—О—Й–µ–≥–Њ —З–ї–µ–љ–∞ –∞—Б–Є–Љ–њ—В–Њ—В–Є—З–µ—Б–Ї–Њ–≥–Њ —А–∞–Ј–ї–Њ–ґ–µ–љ–Є—П –њ–Њ–Ј–≤–Њ–ї—П–µ—В –Ј–љ–∞—З–Є—В–µ–ї—М–љ–Њ —Г—В–Њ—З–љ–Є—В—М —А–µ–Ј—Г–ї—М—В–∞—В. –Ф–ї—П —Д—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П –љ—Г–ї–µ–≤–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞ –Њ–љ –≤—Л–≥–ї—П–і–Є—В —Б–ї–µ–і—Г—О—Й–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ:
J
0
→ вЖТ -->
2
π ѕА -->
x
cos
вБ° -->
(
x
− вИТ -->
π ѕА -->
4
)
+
1
4
x
2
π ѕА -->
x
sin
вБ° -->
(
x
− вИТ -->
π ѕА -->
4
)
.
{\displaystyle J_{0}\rightarrow {\sqrt {\frac {2}{\pi x}}}\cos(x-{\frac {\pi }{4}})+{\frac {1}{4x{\sqrt {2\pi x}}}}\sin(x-{\frac {\pi }{4}}).}
–§—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П –Љ–Њ–≥—Г—В –±—Л—В—М –≤—Л—А–∞–ґ–µ–љ—Л —З–µ—А–µ–Ј –≥–Є–њ–µ—А–≥–µ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї—Г—О —Д—Г–љ–Ї—Ж–Є—О :
J
α ќ± -->
(
z
)
=
(
z
/
2
)
α ќ± -->
Γ ќУ -->
(
α ќ± -->
+
1
)
0
F
1
(
α ќ± -->
+
1
;
− вИТ -->
z
2
/
4
)
.
{\displaystyle J_{\alpha }(z)={\frac {(z/2)^{\alpha }}{\Gamma (\alpha +1)}}{}_{0}F_{1}(\alpha +1;-z^{2}/4).}
–Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –њ—А–Є —Ж–µ–ї—Л—Е
α ќ± -->
{\displaystyle \alpha }
–Њ–і–љ–Њ–Ј–љ–∞—З–љ–∞—П –∞–љ–∞–ї–Є—В–Є—З–µ—Б–Ї–∞—П , –∞ –њ—А–Є –љ–µ—Ж–µ–ї—Л—Е вАФ –Љ–љ–Њ–≥–Њ–Ј–љ–∞—З–љ–∞—П –∞–љ–∞–ї–Є—В–Є—З–µ—Б–Ї–∞—П .
–°—Г—Й–µ—Б—В–≤—Г–µ—В –њ—А–µ–і—Б—В–∞–≤–ї–µ–љ–Є–µ –і–ї—П —Д—Г–љ–Ї—Ж–Є–є –С–µ—Б—Б–µ–ї—П –њ–µ—А–≤–Њ–≥–Њ —А–Њ–і–∞ –Є —Ж–µ–ї–Њ–≥–Њ –њ–Њ—А—П–і–Ї–∞ —З–µ—А–µ–Ј –Ї–Њ—Н—Д—Д–Є—Ж–Є–µ–љ—В—Л —А—П–і–∞ –Ы–Њ—А–∞–љ–∞ —Д—Г–љ–Ї—Ж–Є–Є –Њ–њ—А–µ–і–µ–ї—С–љ–љ–Њ–≥–Њ –≤–Є–і–∞, –∞ –Є–Љ–µ–љ–љ–Њ
e
z
2
(
w
− вИТ -->
1
w
)
=
∑ вИС -->
n
=
− вИТ -->
∞ вИЮ -->
+
∞ вИЮ -->
J
n
(
z
)
w
n
.
{\displaystyle e^{{\frac {z}{2}}\left(w-{\frac {1}{w}}\right)}=\sum _{n=-\infty }^{+\infty }J_{n}(z)w^{n}.}
–Я–Њ–ї—Г—З–∞–µ—В—Б—П –Є–Ј –≤—Л—А–∞–ґ–µ–љ–Є—П –і–ї—П –њ—А–Њ–Є–Ј–≤–Њ–і—П—Й–µ–є —Д—Г–љ–Ї—Ж–Є–Є –њ—А–Є
a
=
1
{\displaystyle a=1}
w
=
e
i
ϕ ѕХ -->
{\displaystyle w=e^{i\phi }}
[ 10]
e
i
z
sin
вБ° -->
ϕ ѕХ -->
=
J
0
(
z
)
+
2
∑ вИС -->
n
=
1
∞ вИЮ -->
J
2
n
(
z
)
cos
вБ° -->
(
2
n
ϕ ѕХ -->
)
+
2
i
∑ вИС -->
n
=
1
∞ вИЮ -->
J
2
n
− вИТ -->
1
(
z
)
sin
вБ° -->
(
2
n
− вИТ -->
1
)
ϕ ѕХ -->
.
{\displaystyle e^{iz\sin \phi }=J_{0}(z)+2\sum _{n=1}^{\infty }J_{2n}(z)\cos(2n\phi )+2i\sum _{n=1}^{\infty }J_{2n-1}(z)\sin(2n-1)\phi .}
–Я—А–Є
a
=
1
{\displaystyle a=1}
t
=
i
e
i
ϕ ѕХ -->
{\displaystyle t=ie^{i\phi }}
[ 10]
e
i
z
cos
вБ° -->
ϕ ѕХ -->
=
J
0
(
z
)
+
2
∑ вИС -->
n
=
1
∞ вИЮ -->
i
n
J
n
(
z
)
cos
вБ° -->
(
n
ϕ ѕХ -->
)
.
{\displaystyle e^{iz\cos \phi }=J_{0}(z)+2\sum _{n=1}^{\infty }i^{n}J_{n}(z)\cos(n\phi ).}
–Ф–ї—П —Д—Г–љ–Ї—Ж–Є–є –С–µ—Б—Б–µ–ї—П —Б—Г—Й–µ—Б—В–≤—Г–µ—В —А—П–і —А–µ–Ї—Г—А—А–µ–љ—В–љ—Л—Е —Б–Њ–Њ—В–љ–Њ—И–µ–љ–Є–є. –Я—А–Є–≤–µ–і—С–Љ –Ј–і–µ—Б—М –љ–µ–Ї–Њ—В–Њ—А—Л–µ –Є–Ј –љ–Є—Е:
J
α ќ± -->
+
1
=
α ќ± -->
x
J
α ќ± -->
− вИТ -->
J
α ќ± -->
′
(
x
)
;
{\displaystyle J_{\alpha +1}={\frac {\alpha }{x}}J_{\alpha }-J'_{\alpha }(x);}
J
α ќ± -->
+
1
(
x
)
+
J
α ќ± -->
− вИТ -->
1
(
x
)
=
2
α ќ± -->
x
J
α ќ± -->
(
x
)
;
{\displaystyle J_{\alpha +1}(x)+J_{\alpha -1}(x)={\frac {2\alpha }{x}}J_{\alpha }(x);}
J
α ќ± -->
+
1
(
x
)
− вИТ -->
J
α ќ± -->
− вИТ -->
1
(
x
)
=
− вИТ -->
2
J
α ќ± -->
′
(
x
)
{\displaystyle J_{\alpha +1}(x)-J_{\alpha -1}(x)=-2J'_{\alpha }(x)}
[ 11]
–Ф–ї—П –ї—О–±–Њ–≥–Њ —Ж–µ–ї–Њ–≥–Њ n –Є –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ—Л—Е
z
1
{\displaystyle z_{1}}
z
2
{\displaystyle z_{2}}
[ 12]
J
n
(
z
1
+
z
2
)
=
∑ вИС -->
k
=
− вИТ -->
∞ вИЮ -->
∞ вИЮ -->
J
k
(
z
1
)
J
n
− вИТ -->
k
(
z
2
)
.
{\displaystyle J_{n}(z_{1}+z_{2})=\sum _{k=-\infty }^{\infty }J_{k}(z_{1})J_{n-k}(z_{2}).}
–Ф–ї—П –ї—О–±—Л—Е
a
{\displaystyle a}
b
{\displaystyle b}
[ 13]
∫ вИЂ -->
0
∞ вИЮ -->
e
− вИТ -->
a
t
J
n
(
b
t
)
d
t
=
b
n
a
2
+
b
2
(
a
2
+
b
2
+
a
)
n
.
{\displaystyle \int _{0}^{\infty }e^{-at}J_{n}(bt)\mathrm {d} t={\frac {b^{n}}{{\sqrt {a^{2}+b^{2}}}({\sqrt {a^{2}+b^{2}}}+a)^{n}}}.}
–І–∞—Б—В–љ—Л–Љ —Б–ї—Г—З–∞–µ–Љ –њ–Њ—Б–ї–µ–і–љ–µ–є —Д–Њ—А–Љ—Г–ї—Л —П–≤–ї—П–µ—В—Б—П –≤—Л—А–∞–ґ–µ–љ–Є–µ
∫ вИЂ -->
0
∞ вИЮ -->
e
− вИТ -->
a
t
J
0
(
b
t
)
d
t
=
1
a
2
+
b
2
.
{\displaystyle \int _{0}^{\infty }e^{-at}J_{0}(bt)\mathrm {d} t={\frac {1}{\sqrt {a^{2}+b^{2}}}}.}
вЖС 1 2 –Ч—Г–±–Њ–≤ –Т. –Ш. . –§—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П . вАФ –Ь. : –Ь–§–Ґ–Ш, 2007. –Р—А—Е–Є–≤–Є—А–Њ–≤–∞–љ–Њ 24 –Є—О–љ—П 2016 –≥–Њ–і–∞.вЖС –°–Є–љ—Г—Б –≤ —Б—В–µ–њ–µ–љ–Є —Г —Н–Ї—Б–њ–Њ–љ–µ–љ—В—Л. –Ш—Б–њ—А–∞–≤–Є—В—М?
вЖС Abramowitz and Stegun, p. 437, 10.1.1 –Р—А—Е–Є–≤–љ–∞—П –Ї–Њ–њ–Є—П –Њ—В 2 —Б–µ–љ—В—П–±—А—П 2006 –љ–∞ Wayback Machine .
вЖС Abramowitz and Stegun, p. 439, 10.1.25, 10.1.26 –Р—А—Е–Є–≤–љ–∞—П –Ї–Њ–њ–Є—П –Њ—В 21 –і–µ–Ї–∞–±—А—П 2009 –љ–∞ Wayback Machine .
вЖС Abramowitz and Stegun, p. 438, 10.1.11 –Р—А—Е–Є–≤–љ–∞—П –Ї–Њ–њ–Є—П –Њ—В 30 –∞–њ—А–µ–ї—П 2009 –љ–∞ Wayback Machine .
вЖС Abramowitz and Stegun, p. 438, 10.1.12 –Р—А—Е–Є–≤–љ–∞—П –Ї–Њ–њ–Є—П –Њ—В 30 –∞–њ—А–µ–ї—П 2009 –љ–∞ Wayback Machine .
вЖС Abramowitz and Stegun, p. 439, 10.1.39 –Р—А—Е–Є–≤–љ–∞—П –Ї–Њ–њ–Є—П –Њ—В 21 –і–µ–Ї–∞–±—А—П 2009 –љ–∞ Wayback Machine .
вЖС Abramowitz and Stegun, p. 439, 10.1.23, 10.1.24 –Р—А—Е–Є–≤–љ–∞—П –Ї–Њ–њ–Є—П –Њ—В 22 –і–µ–Ї–∞–±—А—П 2019 –љ–∞ Wayback Machine .
вЖС Arfken G. B., Hans J. W. . Mathematical Methods for Physicists. 6th ed. вАФ San Diego: Harcourt, 2005. вАФ ISBN 0-12-059876-0 .вЖС 1 2 –С–µ–є—В–Љ–µ–љ, –≠—А–і–µ–є–Є, 1974 , —Б. 15.вЖС –Т. –°. –У–∞–≤—А–Є–ї–Њ–≤ –Є –і—А. –§—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П –≤ –Ј–∞–і–∞—З–∞—Е –Љ–∞—В–µ–Љ–∞—В–Є—З–µ—Б–Ї–Њ–є —Д–Є–Ј–Є–Ї–Є –Р—А—Е–Є–≤–љ–∞—П –Ї–Њ–њ–Є—П –Њ—В 26 –љ–Њ—П–±—А—П 2019 –љ–∞ Wayback Machine , —Б—В—А. 7
вЖС –Ы–∞–≤—А–µ–љ—В—М–µ–≤, –®–∞–±–∞—В, 1973 , —Б. 670.вЖС –Ы–∞–≤—А–µ–љ—В—М–µ–≤, –®–∞–±–∞—В, 1973 , —Б. 671.
–Т–∞—В—Б–Њ–љ –У. . –Ґ–µ–Њ—А–Є—П –±–µ—Б—Б–µ–ї–µ–≤—Л—Е —Д—Г–љ–Ї—Ж–Є–є. вАФ –Ь. : –Ш–Ы , 1949.–С–µ–є—В–Љ–µ–љ –У., –≠—А–і–µ–є–Є –Р. . –§—Г–љ–Ї—Ж–Є–Є –С–µ—Б—Б–µ–ї—П, —Д—Г–љ–Ї—Ж–Є–Є –њ–∞—А–∞–±–Њ–ї–Є—З–µ—Б–Ї–Њ–≥–Њ —Ж–Є–ї–Є–љ–і—А–∞, –Њ—А—В–Њ–≥–Њ–љ–∞–ї—М–љ—Л–µ –Љ–љ–Њ–≥–Њ—З–ї–µ–љ—Л // –Т—Л—Б—И–Є–µ —В—А–∞–љ—Б—Ж–µ–љ–і–µ–љ—В–љ—Л–µ —Д—Г–љ–Ї—Ж–Є–Є. –Ґ. 2. 2-–µ –Є–Ј–і / –Я–µ—А. —Б –∞–љ–≥–ї. –Э. –ѓ. –Т–Є–ї–µ–љ–Ї–Є–љ–∞. вАФ –Ь. : –Э–∞—Г–Ї–∞ , 1974. вАФ 296 —Б.–Ы–∞–≤—А–µ–љ—В—М–µ–≤ –Ь. –Р., –®–∞–±–∞—В –С. –Т. . –Ь–µ—В–Њ–і—Л —В–µ–Њ—А–Є–Є —Д—Г–љ–Ї—Ж–Є–є –Ї–Њ–Љ–њ–ї–µ–Ї—Б–љ–Њ–≥–Њ –њ–µ—А–µ–Љ–µ–љ–љ–Њ–≥–Њ. вАФ –Ь. : –Э–∞—Г–Ї–∞ , 1973. вАФ 736 —Б.




























































![{\displaystyle Y_{\alpha }(x)\rightarrow \left\{{\begin{matrix}{\frac {2}{\pi }}\left[\ln(x/2)+\gamma \right]&{\mbox{;}}\quad \alpha =0\\\\-{\frac {\Gamma (\alpha )}{\pi }}\left({\frac {2}{x}}\right)^{\alpha }&{\mbox{;}}\quad \alpha >0\end{matrix}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1eb6771d58e00f185086b14f2e686fe00e9aedc3)






















