аЃбаАаВаНаЕаНаИаЕ ааАаПаЛаАбаА
|
Read other articles:

Ryusuke Kawasaki (хЗхД щОфЛcode: ja is deprecated , Kawasaki RyХЋsuke, lahir 16 Juli 1953) adalah penyanyi dan aktor asal Jepang. Dia dikenal dengan peran-perannya dalam serial tokusatsu dan drama: sebagai Toyotomi Hideyori dalam Sarutobi Sasuke, dan sebagai Ryuusuke Oowashi / Vul Eagle I dalam serial Super Sentai Taiyou Sentai Sun Vulcan. Diskografi Singel Summer Blues (уЕууМуЛууЋуМуЙ) (Warner Pioneer, 1978) Kokoro ni Umi wo (ууууЋцЕЗу) (Warner Pioneer, 1979) Soyo Kaze...

PolychaetaRentang fosil: 530т0 jtyl Preа а O S D C P T J K Pg N Kambrium (atau sebelumnya?) - sekarang A variety of marine worms: plate from Das Meer by M.J. Schleiden (1804т1881). Klasifikasi ilmiah Kerajaan: Animalia Filum: Annelida Kelas: PolychaetaGrube, 1850 Kelompok yang termasuk Echiura Palpata Scolecida Kelompok yang tidak termasuk Chaetopteridae[1] Polychaeta adalah kelas cacing annelida yang umumnya hidup di laut, sebagian juga ditemukan di sungai dan danau (air ...

School in Pechersk Raion, Kyiv, UkraineNatural Science Lyceum 145Address46 Shota Rustaveli StreetPechersk Raion, Kyiv, 01033UkraineCoordinates50ТА26тВ4тГN 30ТА31тВ3тГE / 50.43444ТАN 30.51750ТАE / 50.43444; 30.51750InformationTypeComprehensive school, Lyceum, Public, Specialized schoolEstablishedSeptember 1, 1962 (1962-09-01)PrincipalLevtyk Mykola MykolayovychGrades8т11Websitewww.lic145.kiev.ua The 145th Natural Science Lyceum, officially known as K...
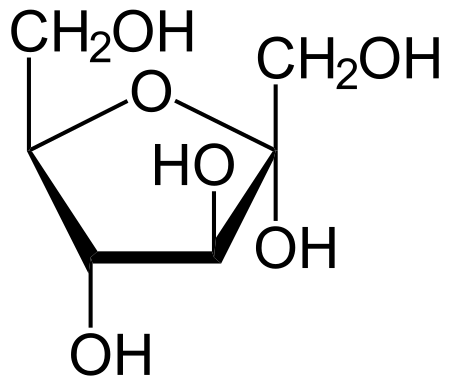
Fruktosa, salah satu jenis monosakarida. Monosakarida (dari Bahasa Yunani mono: satu, sacchar: gula) adalah senyawa karbohidrat dalam bentuk gula yang paling sederhana.[1][2].Gugus fungsi yang menyusun monosakarida adalah satu unit aldehid atau keton. Dalam bentuk stereoisomer, monosakarida memiliki sedikitnya satu atom karbon asimetrik.[3] Monosakarida terbentuk dari hasil sintesis senyawa sederhana melalui proses glukoneogenesis. Pembentukan monosakarida juga dapat d...

Untuk salmon sebagai makanan, lihat Salmon (makanan). Untuk tokoh Alkitab yang bernama Salmon, lihat Salmon (tokoh Alkitab). Ilustrasi salmon pejantan dari beberapa spesies utama salmon Pasifik ketika musim kawin atau bertelur (gambar tidak proporsional dengan perbandingan sesungguhnya) Daging salmon alaska putih Salmon atau salem adalah jenis ikan dari famili Salmonidae. Ikan lain yang berada dalam satu famili dengan salmon adalah Trout. Perbedaan kedua jenis ikan tersebut antara lain: salmo...

2015 video gameBroforceDeveloper(s)Free LivesPublisher(s)Devolver DigitalDirector(s)Evan GreenwoodProducer(s)Shaz GreenwoodDesigner(s)Evan GreenwoodDorian DutrieuxProgrammer(s)Evan GreenwoodRuan RothmannRichard PieterseArtist(s)Jarred LuntDawid StraussFilip OrekhovJonathan Hau-YoonDorian DutrieuxDuncan GreenwoodPhilipe RiosComposer(s)Deon van HeerdenEngineUnityPlatform(s)Microsoft WindowsOS XLinuxPlayStation 4Nintendo SwitchXbox OneReleaseWindows, OS X15 October 2015Linux17 October 2015PlayS...

Japanese University in Nishihara, Okinawa, Japan University of the RyukyusччхЄЇхІTypePublic (national)EstablishedMay 22, 1950PresidentMutsumi NishidaAdministrative staff1,265Students8,079Undergraduates7,140Postgraduates860Doctoral students330Other students8LocationNishihara, Nakagami District, Okinawa Prefecture, JapanCampusUrbanAffiliationsASAIHLWebsitewww.u-ryukyu.ac.jp The University of the Ryukyus (ччхЄЇхІ, RyХЋkyХЋ Daigaku), abbreviated to RyХЋdai (чхЄЇ), is a Japanese nation...

Papuan language spoken in Solomon Islands BiluaNative toSolomon IslandsRegionVella Lavella Island, Western Province.Native speakers(8,700 cited 1999)[1]Language familyCentral Solomon BiluaLanguage codesISO 639-3blbGlottologbilu1245ELPBiluaBilua is not endangered according to the classification system of the UNESCO Atlas of the World's Languages in Danger 7ТА55тВS 156ТА40тВE / 7.92ТАS 156.66ТАE / -7.92; 156.66Bilua (also known as Mbilua or Vella Lavella)&...

ContaultcomuneContault т Veduta LocalizzazioneStato Francia RegioneGrand Est Dipartimento Marna ArrondissementSainte-Menehould CantoneArgonne Suippe et Vesle TerritorioCoordinate48ТА54тВ45тГN 4ТА47тВ27тГE / 48.9125ТАN 4.790833ТАE48.9125; 4.790833яЛП (Contault)Coordinate: 48ТА54тВ45тГN 4ТА47тВ27тГE / 48.9125ТАN 4.790833ТАE48.9125; 4.790833яЛП (Contault) Altitudine150 m s.l.m. Superficie9,33 kmТВ Abitanti74[1] (2009) Densi...

Russian footballer In this name that follows Eastern Slavic naming customs, the patronymic is Nailevich and the family name is Izmailov. Marat Izmailov Izmailov with Krasnodar in 2015Personal informationFull name Marat Nailevich IzmailovDate of birth (1982-09-21) 21 September 1982 (age 41)Place of birth Moscow, Soviet UnionHeight 1.72 m (5 ft 7+1⁄2 in)Position(s) MidfielderSenior career*Years Team Apps (Gls)2000 Lokomotiv B 18 (1)2001т2008 Lokomotiv Moscow 124 ...

Union Army general For other people named Joseph Carr, see Joseph Carr (disambiguation). Joseph Bradford CarrJoseph Bradford CarrSecretary of State of New YorkIn office1880т1885GovernorAlonzo B. Cornell Grover ClevelandDavid B. HillPreceded byAllen C. BeachSucceeded byFrederick Cook Personal detailsBorn(1828-08-16)August 16, 1828Albany, New YorkDiedFebruary 24, 1895(1895-02-24) (aged 66)Troy, New YorkMilitary serviceAllegianceUnited States of AmericaUnionBranch/serviceUnited States Arm...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Results of the 2000 Canadian federal election т news ТЗ newspapers ТЗ books ТЗ scholar ТЗ JSTOR (January 2024)...

абаЛаИбб ааОаНаИббаКаОаГаОабаВбаВ абббаЕаВбббб аІаЕаНбба аАаЙаОаН ааИбаАаКбаВббаКаИаЙааАаЗаВаА аНаА баЕббб ааЛаЕаКбаАаНаДбаА ааОаНаИббаКаОаГаОааОаЛаИбаНб аНаАаЗаВаИ ааЕаКаАбббаКаА аНаИаЖбаА, ааО аЁаАаКбаАаМаЕаНбаОаК, аб аОбаОаНаОаК, ааАаМаМаЕбаВаЕв, аб аОбаОаНаОаК, ааЕаМ'баНаА абаДаНаОаГаОаАаВббббаЙббаКаОаГаО аПаЕббаОаДб (баКбаАбаНббаКаОб) ааЕаКаАбббаКаА аНаИаЖбаАаАаВббббаЙббаКаОаГаО аПаЕббаОаДб (аНбаМаЕб...

ууЎщ чЎуЇуЏуцчцА 1/7 уЋуЄууІшЊЌцууІууОууцЅчБГхМуЎццЅуЋуЄууІуЏу1ц7цЅуууцЌЇхЗхМуЎццЅуЋуЄууІуЏу7ц1цЅууушІЇуу ууу ууЎщ чЎуЋуЏуфИщЈуЎуГуГууЅуМуПущВшІЇуНуууЇшЁЈчЄКуЇууЊуцхяМUnicode5.2уЇшЁЈчОууARIBхЄхяМухЋуОууІууОуяМшЉГчДАяМу 1/7яМ7хуЎ1ууЊуЊуЖууЎууЁуууЁуЖууЎууЁяМуЏу0 уЈ 1 уЎщуЋууцчцАуЇууу 1⁄7=...

Marcus William RobertsonLahir(1870-02-12)12 Februari 1870Flintville, WisconsinMeninggal24 Mei 1948(1948-05-24) (umur 78)Portland, OregonTempat pemakamanPine Grove Cemetery, Hood River, OregonPengabdianAmerika SerikatDinas/cabangAngkatan Darat Amerika SerikatPangkatSersanKesatuanYoung's Scouts, 2nd Oregon Volunteer Infantry RegimentPerang/pertempuranPerang Filipina-AmerikaPerang Dunia IPenghargaanMedal of Honor Marcus William Robertson (12 Februari 1870 – 24 Mei 1948) adal...
Women's 800 metres at the 2022 World ChampionshipsThe finish of the final.VenueHayward FieldDates21 July (heats)22 July (semi-finals)24 July (final)Competitors48 from 29 nationsWinning time1:56.30Medalists Athing Mu United States Keely Hodgkinson Great Britain Mary Moraa Kenya← 20192023 → Video on YouTubeOfficial Video Events at the2022 World ChampionshipsTrack events100 mmenwomen200 mmenwomen4...

йиЈиЇиЁ иЊййиЈйй (иЈиЇййиЇиЈиЇййиЉ:хЄЉхЙГуЎчЋч хЄЇцЕшЁ)и иЃй йиЈиЇиЁ иЇйиЌиЏиБй иЇййиЇиЈиЇййи йй иЃйиЈиБ йиЈиЇиЁ иЌиЏиБй ииЕй йй иЇййиЇиЈиЇй йй йиЊиБиЉ иЊййиЈйй [иЇйиЅйиЌййиВйиЉ] иЈйй иЙиЇй й 735-737й иЃиЕиЇиЈ иЙиЏиЏ йиЈйиБ й й иГйиЇй иЇйиЈйиЇиЏ йиЊиГиЈиЈ иЈййиЇиЉ й иЇ ййиЇиБиЈ иЋйиЋ иДиЙиЈ иЇййиЇиЈиЇй йй иЊйй иЇййиЊиБиЉи йй иЇ иЃиЏй иЅйй иЊиЏиЇиЙйиЇиЊ иЅиЌиЊй иЇиЙйиЉ йиЅйиЊиЕиЇиЏйиЉ йиЏйййиЉ йиЈйиБиЉ иЙ...

йиАй й йиЇйиЉ иКйиБ й иБиЇиЌиЙиЉ. ййиЈиКй иЃй йиВиЇй йиАиЇ иЇййиЇйиЈ иЈиЙиЏ иЃй йиБиЇиЌиЙйиЇ й ииБиБи иЅиАиЇ йиВй иЇйиЃй иБ ййиЌиЈ иЃй иЊйиГй иЇйй йиЇйиЉ иЈййиЇйиЈ иЇйиЕйиЇйиЉ иЇйй йиЇиГиЈиЉ. йй йй иЃйиЖиЇй иЊйиЏйй иЗйиЈ йй иБиЇиЌиЙиЉ иЇйй йиЇйиЉ йй иЇйиЕйииЉ иЇйй иЎиЕиЕиЉ йиАйй. (ййиЇйиБ 2021) йиАй иЇйй йиЇйиЉ йиЊйй иЉ иЅиА иЊиЕй иЅйййиЇ й йиЇйиЇиЊ иЃиЎиБй ййййиЉ иЌиЏйиЇ. йиЖййиЇи иГиЇиЙиЏ иЈиЅиЖиЇйиЉ йяПН...

Nikki Haley Duta Besar Amerika Serikat untuk Perserikatan Bangsa-Bangsa ke-29Masa jabatan25 Januari 2017 т 31 Desember 2018PresidenDonald TrumpWakilMichele J. SisonKelley Eckels Currie (acting)Jonathan CohenPendahuluSamantha PowerPenggantiKelly CraftGubernur South Carolina ke-116Masa jabatan12 Januari 2011 т 24 Januari 2017WakilKen ArdGlenn F. McConnellYancey McGillHenry McMasterPendahuluMark SanfordPenggantiHenry McMasterAnggota Dewan Perwakilan Rakyat South...

хАчНфМЏчЙТЗхЂхЁцЏ Robert Emerson Lucas Jr.хКч(1937-09-15)1937хЙД9ц15цЅ чОхНшЏчщ хЗщ хКщІЌщфИ2023хЙД5ц15цЅ(2023цВт05т15)яМ85цВяМ чОхНфМхЉшЋОфМхЗшх хЅхНчБ чОхНщ хЖRita CohenяМ1959хЙДчЛхЉяМхЗВщЂхЉяМххИТЗцЏцхКяМшБшЏяМNancy StokeyяМхПхЅГ2ч чЉЖцКцхЁх ЇхКчОщхЄЇхИшх хЅхЄЇхИч чЉЖщЂхчИНщЋчЖцПхИхІцДОцАшхЄх ИчЖцПхИцДОцЏц Ёшх хЅхЄЇхИяМBAуMAуPhDяМххЃЋхАхИЋHТЗц МщЗц МТЗхц...

















