![]() –ď–į—Ä–ľ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ł–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł
–ď–į—Ä–ľ–ĺ–Ĺ–ł—á–Ķ—Ā–ļ–ł–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł
–°—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź—é—ā —Ā–ĺ–Ī–ĺ–Ļ —É–≥–Ľ–ĺ–≤—É—é —á–į—Ā—ā—Ć —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į –ĺ—Ä—ā–ĺ–≥–ĺ–Ĺ–į–Ľ—Ć–Ĺ—č—Ö —Ä–Ķ—ą–Ķ–Ĺ–ł–Ļ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –õ–į–Ņ–Ľ–į—Ā–į, –∑–į–Ņ–ł—Ā–į–Ĺ–Ĺ—É—é –≤ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł—Ö –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į—Ö. –ě–Ĺ–ł —ą–ł—Ä–ĺ–ļ–ĺ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑—É—é—ā—Ā—Ź –ī–Ľ—Ź –ł–∑—É—á–Ķ–Ĺ–ł—Ź —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł—Ö
—Ź–≤–Ľ–Ķ–Ĺ–ł–Ļ –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č—Ö –ĺ–Ī–Ľ–į—Ā—ā—Ź—Ö, –ĺ–≥—Ä–į–Ĺ–ł—á–Ķ–Ĺ–Ĺ—č—Ö —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–ľ–ł
–Ņ–ĺ–≤–Ķ—Ä—Ö–Ĺ–ĺ—Ā—ā—Ź–ľ–ł –ł –Ņ—Ä–ł —Ä–Ķ—ą–Ķ–Ĺ–ł–ł —Ą–ł–∑–ł—á–Ķ—Ā–ļ–ł—Ö –∑–į–ī–į—á, –ĺ–Ī–Ľ–į–ī–į—é—Č–ł—Ö
—Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł–ľ–ľ–Ķ—ā—Ä–ł–Ķ–Ļ.
–°—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –ł–ľ–Ķ—é—ā –Ī–ĺ–Ľ—Ć—ą–ĺ–Ķ –∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ –≤ —ā–Ķ–ĺ—Ä–ł–ł –ī–ł—Ą—Ą–Ķ—Ä–Ķ–Ĺ—Ü–ł–į–Ľ—Ć–Ĺ—č—Ö —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł–Ļ –≤ —á–į—Ā—ā–Ĺ—č—Ö –Ņ—Ä–ĺ–ł–∑–≤–ĺ–ī–Ĺ—č—Ö –ł —ā–Ķ–ĺ—Ä–Ķ—ā–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą–ł–∑–ł–ļ–Ķ, –≤ —á–į—Ā—ā–Ĺ–ĺ—Ā—ā–ł –≤ –∑–į–ī–į—á–į—Ö —Ä–į—Ā—á—Ď—ā–į —ć–Ľ–Ķ–ļ—ā—Ä–ĺ–Ĺ–Ĺ—č—Ö –ĺ—Ä–Ī–ł—ā–į–Ľ–Ķ–Ļ –≤ –į—ā–ĺ–ľ–Ķ, –≥—Ä–į–≤–ł—ā–į—Ü–ł–ĺ–Ĺ–Ĺ–ĺ–≥–ĺ –Ņ–ĺ–Ľ—Ź –≥–Ķ–ĺ–ł–ī–į, –ľ–į–≥–Ĺ–ł—ā–Ĺ–ĺ–≥–ĺ –Ņ–ĺ–Ľ—Ź –Ņ–Ľ–į–Ĺ–Ķ—ā –ł –ł–Ĺ—ā–Ķ–Ĺ—Ā–ł–≤–Ĺ–ĺ—Ā—ā–ł —Ä–Ķ–Ľ–ł–ļ—ā–ĺ–≤–ĺ–≥–ĺ –ł–∑–Ľ—É—á–Ķ–Ĺ–ł—Ź.
–ě–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł–Ķ
 –í–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł Ylm, l=0‚Ķ4 (—Ā–≤–Ķ—Ä—Ö—É –≤–Ĺ–ł–∑), m=0‚Ķ4 (—Ā–Ľ–Ķ–≤–į –Ĺ–į–Ņ—Ä–į–≤–ĺ). –§—É–Ĺ–ļ—Ü–ł–ł –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ–į Yl-m –Ņ–ĺ–≤—Ď—Ä–Ĺ—É—ā—č –≤–ĺ–ļ—Ä—É–≥ –ĺ—Ā–ł Z –Ĺ–į 90/m –≥—Ä–į–ī—É—Ā–ĺ–≤ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ —Ą—É–Ĺ–ļ—Ü–ł–Ļ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ–į.
–í–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł Ylm, l=0‚Ķ4 (—Ā–≤–Ķ—Ä—Ö—É –≤–Ĺ–ł–∑), m=0‚Ķ4 (—Ā–Ľ–Ķ–≤–į –Ĺ–į–Ņ—Ä–į–≤–ĺ). –§—É–Ĺ–ļ—Ü–ł–ł –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ–į Yl-m –Ņ–ĺ–≤—Ď—Ä–Ĺ—É—ā—č –≤–ĺ–ļ—Ä—É–≥ –ĺ—Ā–ł Z –Ĺ–į 90/m –≥—Ä–į–ī—É—Ā–ĺ–≤ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ —Ą—É–Ĺ–ļ—Ü–ł–Ļ –Ņ–ĺ–Ľ–ĺ–∂–ł—ā–Ķ–Ľ—Ć–Ĺ–ĺ–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ–į.
–°—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —Ā–ĺ–Ī—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–ľ–ł —Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ–ł –ĺ–Ņ–Ķ—Ä–į—ā–ĺ—Ä–į –õ–į–Ņ–Ľ–į—Ā–į –≤ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā (–ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł–Ķ  ). –ě–Ĺ–ł –ĺ–Ī—Ä–į–∑—É—é—ā –ĺ—Ä—ā–ĺ–Ĺ–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—É—é —Ā–ł—Ā—ā–Ķ–ľ—É –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ —Ą—É–Ĺ–ļ—Ü–ł–Ļ –Ĺ–į —Ā—Ą–Ķ—Ä–Ķ
). –ě–Ĺ–ł –ĺ–Ī—Ä–į–∑—É—é—ā –ĺ—Ä—ā–ĺ–Ĺ–ĺ—Ä–ľ–ł—Ä–ĺ–≤–į–Ĺ–Ĺ—É—é —Ā–ł—Ā—ā–Ķ–ľ—É –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ —Ą—É–Ĺ–ļ—Ü–ł–Ļ –Ĺ–į —Ā—Ą–Ķ—Ä–Ķ  –≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ:
–≤ —ā—Ä—Ď—Ö–ľ–Ķ—Ä–Ĺ–ĺ–ľ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ:

 ,
,
–≥–ī–Ķ * –ĺ–Ī–ĺ–∑–Ĺ–į—á–į–Ķ—ā –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ–Ķ —Ā–ĺ–Ņ—Ä—Ź–∂–Ķ–Ĺ–ł–Ķ,  ‚ÄĒ —Ā–ł–ľ–≤–ĺ–Ľ –ö—Ä–ĺ–Ĺ–Ķ–ļ–Ķ—Ä–į.
‚ÄĒ —Ā–ł–ľ–≤–ĺ–Ľ –ö—Ä–ĺ–Ĺ–Ķ–ļ–Ķ—Ä–į.
–°—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –ł–ľ–Ķ—é—ā –≤–ł–ī
 ,
,
–≥–ī–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł  —Ź–≤–Ľ—Ź—é—ā—Ā—Ź —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź–ľ–ł —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź
—Ź–≤–Ľ—Ź—é—ā—Ā—Ź —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź–ľ–ł —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź

–ł –ł–ľ–Ķ—é—ā –≤–ł–ī

–ó–ī–Ķ—Ā—Ć  ‚ÄĒ –Ņ—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ď–Ĺ–Ĺ—č–Ķ –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ—č –õ–Ķ–∂–į–Ĺ–ī—Ä–į, –į
‚ÄĒ –Ņ—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ď–Ĺ–Ĺ—č–Ķ –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ—č –õ–Ķ–∂–į–Ĺ–ī—Ä–į, –į  ‚ÄĒ —Ą–į–ļ—ā–ĺ—Ä–ł–į–Ľ.
‚ÄĒ —Ą–į–ļ—ā–ĺ—Ä–ł–į–Ľ.
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ–Ķ–Ĺ–Ĺ—č–Ķ –ľ–Ĺ–ĺ–≥–ĺ—á–Ľ–Ķ–Ĺ—č –õ–Ķ–∂–į–Ĺ–ī—Ä–į —Ā –ĺ—ā—Ä–ł—Ü–į—ā–Ķ–Ľ—Ć–Ĺ—č–ľ  –∑–ī–Ķ—Ā—Ć –≤–≤–ĺ–ī—Ź—ā—Ā—Ź –ļ–į–ļ
–∑–ī–Ķ—Ā—Ć –≤–≤–ĺ–ī—Ź—ā—Ā—Ź –ļ–į–ļ

–†–Ķ—ą–Ķ–Ĺ–ł–Ķ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź –õ–į–Ņ–Ľ–į—Ā–į –≤ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł—Ö –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā–į—Ö –Ķ—Ā—ā—Ć —ā–į–ļ –Ĺ–į–∑—č–≤–į–Ķ–ľ–į—Ź —ą–į—Ä–ĺ–≤–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź, –Ņ–ĺ–Ľ—É—á–į–Ķ–ľ–į—Ź —É–ľ–Ĺ–ĺ–∂–Ķ–Ĺ–ł–Ķ–ľ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł –Ĺ–į —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ —Ä–į–ī–ł–į–Ľ—Ć–Ĺ–ĺ–≥–ĺ —É—Ä–į–≤–Ĺ–Ķ–Ĺ–ł—Ź.
–í–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–į—Ź —Ą–ĺ—Ä–ľ–į
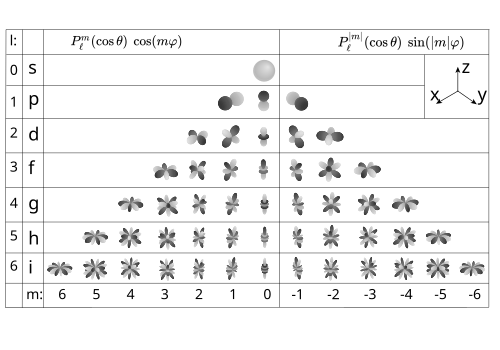 –í–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –ī–ĺ —ą–Ķ—Ā—ā–ĺ–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ–į
–í–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –ī–ĺ —ą–Ķ—Ā—ā–ĺ–≥–ĺ –Ņ–ĺ—Ä—Ź–ī–ļ–į
–Ē–Ľ—Ź —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ —Ą–ĺ—Ä–ľ–į –∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ĺ—ā —É–≥–Ľ–į  ‚ÄĒ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–į—Ź —ć–ļ—Ā–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā–į. –ė—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź —Ą–ĺ—Ä–ľ—É–Ľ—É –≠–Ļ–Ľ–Ķ—Ä–į, –ľ–ĺ–∂–Ĺ–ĺ –≤–≤–Ķ—Ā—ā–ł –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł. –ė–Ĺ–ĺ–≥–ī–į –ł—Ö —É–ī–ĺ–Ī–Ĺ–Ķ–Ķ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć –≤ —Ā–≤—Ź–∑–ł —Ā —ā–Ķ–ľ, —á—ā–ĺ –ĺ–Ĺ–ł –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –Ĺ–į–≥–Ľ—Ź–ī–Ĺ–ĺ –Ņ–ĺ–ļ–į–∑–į–Ĺ—č –Ĺ–į –ł–Ľ–Ľ—é—Ā—ā—Ä–į—Ü–ł—Ź—Ö, –≤ –ĺ—ā–Ľ–ł—á–ł–Ķ –ĺ—ā –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č—Ö. –ě–ī–Ĺ–į–ļ–ĺ –∑–Ĺ–į—á–ł–ľ–ĺ–Ķ —É–ī–ĺ–Ī—Ā—ā–≤–ĺ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ (—É—ā—Ä–į—á–ł–≤–į–Ķ–ľ–ĺ–Ķ –Ņ—Ä–ł –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–Ķ –ļ –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–ľ) —Ā–ĺ—Ā—ā–ĺ–ł—ā –≤ –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ļ–≤–į–ī—Ä–į—ā–į –ł—Ö –ľ–ĺ–ī—É–Ľ—Ź
‚ÄĒ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–į—Ź —ć–ļ—Ā–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā–į. –ė—Ā–Ņ–ĺ–Ľ—Ć–∑—É—Ź —Ą–ĺ—Ä–ľ—É–Ľ—É –≠–Ļ–Ľ–Ķ—Ä–į, –ľ–ĺ–∂–Ĺ–ĺ –≤–≤–Ķ—Ā—ā–ł –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł. –ė–Ĺ–ĺ–≥–ī–į –ł—Ö —É–ī–ĺ–Ī–Ĺ–Ķ–Ķ –ł—Ā–Ņ–ĺ–Ľ—Ć–∑–ĺ–≤–į—ā—Ć –≤ —Ā–≤—Ź–∑–ł —Ā —ā–Ķ–ľ, —á—ā–ĺ –ĺ–Ĺ–ł –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –Ĺ–į–≥–Ľ—Ź–ī–Ĺ–ĺ –Ņ–ĺ–ļ–į–∑–į–Ĺ—č –Ĺ–į –ł–Ľ–Ľ—é—Ā—ā—Ä–į—Ü–ł—Ź—Ö, –≤ –ĺ—ā–Ľ–ł—á–ł–Ķ –ĺ—ā –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č—Ö. –ě–ī–Ĺ–į–ļ–ĺ –∑–Ĺ–į—á–ł–ľ–ĺ–Ķ —É–ī–ĺ–Ī—Ā—ā–≤–ĺ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ (—É—ā—Ä–į—á–ł–≤–į–Ķ–ľ–ĺ–Ķ –Ņ—Ä–ł –Ņ–Ķ—Ä–Ķ—Ö–ĺ–ī–Ķ –ļ –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–ľ) —Ā–ĺ—Ā—ā–ĺ–ł—ā –≤ –Ĺ–Ķ–∑–į–≤–ł—Ā–ł–ľ–ĺ—Ā—ā–ł –ļ–≤–į–ī—Ä–į—ā–į –ł—Ö –ľ–ĺ–ī—É–Ľ—Ź  –ĺ—ā —É–≥–Ľ–į
–ĺ—ā —É–≥–Ľ–į  .
.
![{\displaystyle {\begin{aligned}Y_{\ell m}&={\begin{cases}\displaystyle {i \over {\sqrt {2}}}\left(Y_{\ell }^{m}-(-1)^{m}\,Y_{\ell }^{-m}\right)&{\text{ }}\ m<0\\\displaystyle Y_{\ell }^{0}&{\text{ }}\ m=0\\\displaystyle {1 \over {\sqrt {2}}}\left(Y_{\ell }^{-m}+(-1)^{m}\,Y_{\ell }^{m}\right)&{\text{ }}\ m>0.\end{cases}}\\&={\begin{cases}\displaystyle {\sqrt {2}}\,(-1)^{m}\,\operatorname {Im} [{Y_{\ell }^{|m|}}]&{\text{ }}\ m<0\\\displaystyle Y_{\ell }^{0}&{\text{ }}\ m=0\\\displaystyle {\sqrt {2}}\,(-1)^{m}\,\operatorname {Re} [{Y_{\ell }^{m}}]&{\text{ }}\ m>0.\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35f77a55bfe53007193bf360c5fb1f53c55011f9)
–ě–Ī—Ä–į—ā–Ĺ–ĺ–Ķ –Ņ—Ä–Ķ–ĺ–Ī—Ä–į–∑–ĺ–≤–į–Ĺ–ł–Ķ:

–ė–Ĺ–ĺ–≥–ī–į –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł –Ĺ–į–∑—č–≤–į—é—ā –∑–ĺ–Ĺ–į–Ľ—Ć–Ĺ—č–ľ–ł, —ā–Ķ—Ā—Ā–Ķ—Ä–į–Ľ—Ć–Ĺ—č–ľ–ł –ł —Ā–Ķ–ļ—ā–ĺ—Ä–ł–į–Ľ—Ć–Ĺ—č–ľ–ł[1].
–§—É–Ĺ–ļ—Ü–ł–ł —Ā m > 0 –∑–į–≤–ł—Ā—Ź—ā –ĺ—ā —É–≥–Ľ–į –ļ–į–ļ –ļ–ĺ—Ā–ł–Ĺ—É—Ā, –į —Ā m < 0 ‚ÄĒ –ļ–į–ļ —Ā–ł–Ĺ—É—Ā.

–ü–ĺ–≤–ĺ—Ä–ĺ—ā—č
 –ü–ĺ–≤–ĺ—Ä–ĺ—ā –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł —Ā m=0 –ł l=3. –ö–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā—č –Ĺ–Ķ —Ä–į–≤–Ĺ—č D-–ľ–į—ā—Ä–ł—Ü–į–ľ –í–ł–≥–Ĺ–Ķ—Ä–į, –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –Ņ–ĺ–ļ–į–∑–į–Ĺ—č –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł, –Ĺ–ĺ –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ—č –Ņ—Ä–ł –Ņ–Ķ—Ä–Ķ—Ä–į–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł–ł –Ņ–ĺ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č–ľ —Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ
–ü–ĺ–≤–ĺ—Ä–ĺ—ā –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ–Ļ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ĺ–Ļ —Ą—É–Ĺ–ļ—Ü–ł–ł —Ā m=0 –ł l=3. –ö–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā—č –Ĺ–Ķ —Ä–į–≤–Ĺ—č D-–ľ–į—ā—Ä–ł—Ü–į–ľ –í–ł–≥–Ĺ–Ķ—Ä–į, –Ņ–ĺ—Ā–ļ–ĺ–Ľ—Ć–ļ—É –Ņ–ĺ–ļ–į–∑–į–Ĺ—č –≤–Ķ—Č–Ķ—Ā—ā–≤–Ķ–Ĺ–Ĺ—č–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł, –Ĺ–ĺ –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –Ņ–ĺ–Ľ—É—á–Ķ–Ĺ—č –Ņ—Ä–ł –Ņ–Ķ—Ä–Ķ—Ä–į–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł–ł –Ņ–ĺ –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ—č–ľ —Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ –Ņ–ĺ–≤–ĺ—Ä–ĺ—ā —Ā–ł—Ā—ā–Ķ–ľ—č –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā  , –Ĺ–į –£–≥–Ľ—č –≠–Ļ–Ľ–Ķ—Ä–į
, –Ĺ–į –£–≥–Ľ—č –≠–Ļ–Ľ–Ķ—Ä–į  –ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ņ—Ä–Ķ–ĺ–Ī—Äa–∑—É–Ķ—ā –Ķ–ī–ł–Ĺ–ł—á–Ĺ—č–Ļ –≤–Ķ–ļ—ā–ĺ—Ä
–ļ–ĺ—ā–ĺ—Ä—č–Ļ –Ņ—Ä–Ķ–ĺ–Ī—Äa–∑—É–Ķ—ā –Ķ–ī–ł–Ĺ–ł—á–Ĺ—č–Ļ –≤–Ķ–ļ—ā–ĺ—Ä  –≤ –≤–Ķ–ļ—ā–ĺ—Ä
–≤ –≤–Ķ–ļ—ā–ĺ—Ä  .
–ü—Ä–ł —ć—ā–ĺ–ľ —É–≥–Ľ—č
.
–ü—Ä–ł —ć—ā–ĺ–ľ —É–≥–Ľ—č  –≤–Ķ–ļ—ā–ĺ—Ä–į
–≤–Ķ–ļ—ā–ĺ—Ä–į  –≤ –Ĺ–ĺ–≤–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –≤—č—Ä–į–∂–į—é—ā—Ā—Ź —á–Ķ—Ä–Ķ–∑ —É–≥–Ľ—č –≤ —Ā—ā–į—Ä–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ
–≤ –Ĺ–ĺ–≤–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā –≤—č—Ä–į–∂–į—é—ā—Ā—Ź —á–Ķ—Ä–Ķ–∑ —É–≥–Ľ—č –≤ —Ā—ā–į—Ä–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ


–í –Ĺ–ĺ–≤–ĺ–Ļ —Ā–ł—Ā—ā–Ķ–ľ–Ķ –ļ–ĺ–ĺ—Ä–ī–ł–Ĺ–į—ā —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź —Ā –ł–Ĺ–ī–Ķ–ļ—Ā–į–ľ–ł  –ł
–ł  –Ī—É–ī–Ķ—ā –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł–ľ–į –≤ –≤–ł–ī–Ķ –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ļ –ļ–ĺ–ľ–Ī–ł–Ĺ–į—Ü–ł–ł –≤—Ā–Ķ—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ —Ā —ā–Ķ–ľ –∂–Ķ –Ĺ–ĺ–ľ–Ķ—Ä–ĺ–ľ
–Ī—É–ī–Ķ—ā –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł–ľ–į –≤ –≤–ł–ī–Ķ –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ļ –ļ–ĺ–ľ–Ī–ł–Ĺ–į—Ü–ł–ł –≤—Ā–Ķ—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ —Ā —ā–Ķ–ľ –∂–Ķ –Ĺ–ĺ–ľ–Ķ—Ä–ĺ–ľ  –ł —Ä–į–∑–Ľ–ł—á–Ĺ—č–ľ–ł
–ł —Ä–į–∑–Ľ–ł—á–Ĺ—č–ľ–ł  . –ö–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā–į–ľ–ł –≤ –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ļ –ļ–ĺ–ľ–Ī–ł–Ĺ–į—Ü–ł–ł —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ- —Ā–ĺ–Ņ—Ä—Ź–∂–Ķ–Ĺ–Ĺ—č–Ķ D-–ľ–į—ā—Ä–ł—Ü—č –í–ł–≥–Ĺ–Ķ—Ä–į[2]
. –ö–ĺ—ć—Ą—Ą–ł—Ü–ł–Ķ–Ĺ—ā–į–ľ–ł –≤ –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ĺ–Ļ –ļ–ĺ–ľ–Ī–ł–Ĺ–į—Ü–ł–ł —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –ļ–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–ĺ- —Ā–ĺ–Ņ—Ä—Ź–∂–Ķ–Ĺ–Ĺ—č–Ķ D-–ľ–į—ā—Ä–ł—Ü—č –í–ł–≥–Ĺ–Ķ—Ä–į[2]
![{\displaystyle {\hat {D}}(\alpha ,\beta ,\gamma )Y_{l}^{m}(\theta ,\varphi )=Y_{\ell }^{m}(\theta ',\varphi ')=\sum _{m'=-\ell }^{\ell }[D_{mm'}^{(\ell )}(\alpha ,\beta ,\gamma )]^{*}Y_{\ell }^{m'}(\theta ,\varphi ),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b4af9fcca20b758b54bfd7755fd70c1232a8854)
–°—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–Ķ —Ą—É–Ĺ–ļ—Ü–ł–ł —Ā –Ĺ–ĺ–ľ–Ķ—Ä–ĺ–ľ  –ĺ–Ī—Ä–į–∑—É—é—ā –Ī–į–∑–ł—Ā –Ĺ–Ķ–Ņ—Ä–ł–≤–ĺ–ī–ł–ľ–ĺ–≥–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł—Ź —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł
–ĺ–Ī—Ä–į–∑—É—é—ā –Ī–į–∑–ł—Ā –Ĺ–Ķ–Ņ—Ä–ł–≤–ĺ–ī–ł–ľ–ĺ–≥–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–ł—Ź —Ä–į–∑–ľ–Ķ—Ä–Ĺ–ĺ—Ā—ā–ł  –≥—Ä—É–Ņ–Ņ—č –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ SO(3).
–≥—Ä—É–Ņ–Ņ—č –≤—Ä–į—Č–Ķ–Ĺ–ł–Ļ SO(3).
–†–į–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –Ņ–Ľ–ĺ—Ā–ļ–ĺ–Ļ –≤–ĺ–Ľ–Ĺ—č –Ņ–ĺ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–ľ —Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ
–ö–ĺ–ľ–Ņ–Ľ–Ķ–ļ—Ā–Ĺ–į—Ź —ć–ļ—Ā–Ņ–ĺ–Ĺ–Ķ–Ĺ—ā–į –ľ–ĺ–∂–Ķ—ā –Ī—č—ā—Ć –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ–Ķ–Ĺ–į –≤ –≤–ł–ī–Ķ —Ä–į–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –Ņ–ĺ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł–ľ —Ą—É–Ĺ–ļ—Ü–ł—Ź–ľ

–ó–ī–Ķ—Ā—Ć  ‚ÄĒ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź –Ď–Ķ—Ā—Ā–Ķ–Ľ—Ź
‚ÄĒ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–į—Ź —Ą—É–Ĺ–ļ—Ü–ł—Ź –Ď–Ķ—Ā—Ā–Ķ–Ľ—Ź
–†–į–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ļ —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ
–†–į–∑–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź –ö–Ľ–Ķ–Ī—ą–į-–ď–ĺ—Ä–ī–į–Ĺ–į –ī–Ľ—Ź –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ļ –ī–≤—É—Ö —Ā—Ą–Ķ—Ä–ł—á–Ķ—Ā–ļ–ł—Ö —Ą—É–Ĺ–ļ—Ü–ł–Ļ –≤—č–≥–Ľ—Ź–ī—Ź—ā —Ā–Ľ–Ķ–ī—É—é—Č–ł–ľ –ĺ–Ī—Ä–į–∑–ĺ–ľ [3]:

–°–ľ. —ā–į–ļ–∂–Ķ
–ü—Ä–ł–ľ–Ķ—á–į–Ĺ–ł—Ź
–õ–ł—ā–Ķ—Ä–į—ā—É—Ä–į
–ü—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–ł—Ź
–°—Ā—č–Ľ–ļ–ł
 –°—Ā—č–Ľ–ļ–ł –Ĺ–į –≤–Ĺ–Ķ—ą–Ĺ–ł–Ķ —Ä–Ķ—Ā—É—Ä—Ā—č |
|---|
–Ę–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł–Ķ —Ā–į–Ļ—ā—č | |
|---|
| –°–Ľ–ĺ–≤–į—Ä–ł –ł —ć–Ĺ—Ü–ł–ļ–Ľ–ĺ–Ņ–Ķ–ī–ł–ł | |
|---|