Фридрих, Томас (математик)
| |||||||||||||||||||||||||||
Read other articles:

Fan Li Fan Li (Hanzi: 范蠡) (hidup sekitar tahun 400an SM) adalah seorang tokoh legendaris yang hidup pada zaman musim semi dan gugur (春秋時代), Dinasti Zhou sebuah masa dimana Tiongkok terpecah atas beberapa negara feodal yang saling berperang. Dia dikenal sebagai politikus penuh visi, ahli strategi perang, penasihat yang baik dan negarawan ulung yang mengabdi pada Raja Goujian dari Yue (越王勾践) untuk bangkit dari kehancuran dan menjadi penguasa di daratan tengah. Setelah mengun...

This article is about mass. For radius, see List of largest known stars. This is a list of the most massive stars that have been discovered, in solar mass units (M☉). Uncertainties and caveats Most of the masses listed below are contested and, being the subject of current research, remain under review and subject to constant revision of their masses and other characteristics. Indeed, many of the masses listed in the table below are inferred from theory, using difficult measurements of...

Election 1954 South Carolina Democratic gubernatorial primary ← 1950 Summer 1954 1958 → Nominee George Timmerman Lester L. Bates Party Democratic Democratic Popular vote 185,541 116,942 Percentage 61.3% 38.7% County resultsTimmerman: 50-60% 60-70% 70-80% 80-90%Bates: 50-60% 80-90% G...

Group of higher educational institution in India Institutes of EminenceFormation2016TypeHigher-education recognition schemeRegion served Republic of IndiaMembership Universities and institutes of higher educationWebsiteioe.ugc.ac.in Institutes of Eminence (IoE) is a recognition scheme for higher education institutes in India, set by the University Grants Commission in 2017. The plan encompasses twenty institutions, twelve of which have already been declared Institutes of Eminence as of April&...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Pretty Little Head song – news · newspapers · books · scholar · JSTOR (April 2018) (Learn how and when to remove this message) 1986 single by Paul McCartneyPretty Little HeadUK front coverSingle by Paul McCartneyfrom the album Press to Play B-sideWrite Awa...

Defunct Czechoslovak newspaper Not to be confused with Právo. Rudé právoProletáři všech zemí, spojte se!First edition of Rudé právo from 21 September 1920TypeDaily newspaperFormatBroadsheetOwner(s)Communist Party of CzechoslovakiaFoundedSeptember 21, 1920 (1920-09-21)Political alignmentCommunistLanguageCzechCeased publicationSeptember 1995HeadquartersPrague, CzechoslovakiaCountryCzechoslovakiaISSN0032-6569 Rudé právo (Czech for Red Justice or The Red Right) was ...

Mel Brooks alla cerimonia in cui ricevette la stella della Hollywood Walk of Fame nel 2010 Oscar alla migliore sceneggiatura originale 1969 Oscar alla carriera 2024 Mel Brooks, pseudonimo di Melvin James Brooks (nato Melvin James Kaminsky[1]; New York, 28 giugno 1926), è un regista, sceneggiatore, comico, compositore, produttore cinematografico, teatrale, televisivo e attore statunitense. È noto per le sue parodie e le sue commedie farsesche. Fa parte dei 19 artisti che hanno conseg...

Political party in France Parts of this article (those related to elected officials, events in recent years) need to be updated. Please help update this article to reflect recent events or newly available information. (March 2021) VIA | The Way of the People VIA | la voie du peupleFounded27 February 2001Split fromUnion for French DemocracyHeadquartersParisIdeologyChristian democracySocial conservatismChristian rightSoft EuroscepticismPolitical positionRight-wing[1]National a...

Political news talk show hosted by Dave Rubin The Rubin ReportGenrePolitical commentaryCreated byDave RubinDavid JanetPresented byDave RubinCountry of originUnited StatesOriginal languageEnglishProductionExecutive producerDavid Janet[1]Production locationLos Angeles, CaliforniaCamera setupMulti-CameraProduction companiesThe Young Turks 2013–2015RYOT 2015Ora TV 2015–2016Independently Produced 2016–presentOriginal releaseReleaseFebruary 16, 2013 (2013-02-16) –present T...

Shopping mall in California, United StatesJapan CenterExterior of Japan Center East, Hotel Kabuki visible in backgroundLocationSan Francisco, California, United StatesCoordinates37°47′06″N 122°25′48″W / 37.785°N 122.430°W / 37.785; -122.430Opening date1968DeveloperNational-BraemarKinki Nippon RailwayPublic transit accessSF Muni #2 Clement, #3 Jackson, 22 Fillmore, 38 Geary/38R Geary RapidWebsitejapancentersf.com The Japan Center is a shopping...

RiverBois de Sioux RiverThe Bois de Sioux River below the dam of Lake Traverse. Roberts County, South Dakota is at left, and Traverse County, Minnesota is at right.Red River drainage basin, with Bois de Sioux River highlightedPhysical characteristicsSource • locationDam at the foot of Lake Traverse, South Dakota • coordinates45°51′42″N 96°34′23″W / 45.8616667°N 96.5730556°W / 45.8616667; -96.5730556 (Bois d...

War crimes court This article needs to be updated. Please help update this article to reflect recent events or newly available information. (December 2017) Kosovo Specialist ChambersDhomat e Specializuara të Kosovës (Albanian)Специјализована већа Косова (Serbian)Seat of the Specialist ChambersEstablished2017LocationThe Hague, NetherlandsAuthorized byConstitution of KosovoWebsitehttps://www.scp-ks.org/PresidentCurrentlyEkaterina TrendafilovaSince12 January 2017Prosec...
Family of mammals belonging to even-toed ungulates Not to be confused with Capridae. AntilocapridaeTemporal range: Early Miocene–recent PreꞒ Ꞓ O S D C P T J K Pg N Pronghorns in Fort Keogh, Montana Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Mammalia Order: Artiodactyla Suborder: Ruminantia Infraorder: Pecora Family: AntilocapridaeJ. E. Gray, 1866 Type genus AntilocapraOrd, 1815 Genera See text The Antilocapridae are a family of ruminant artioda...

Royal Navy Fleet Air Arm Reserve Squadron This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: 1840 Naval Air Squadron – news · newspapers · books · scholar · JSTOR (March 2022) 1840 Naval Air SquadronActive1944-451951-57[1]Country United KingdomBranch Royal NavyPart ofFleet Air A...

Disambiguazione – Se stai cercando altri significati, vedi Tuono (disambigua). Fulmine nube-suolo a Piracicaba (Brasile) Il tuono è un'onda di pressione provocata dal fulmine che, a seconda della natura del fulmine e della distanza dall'osservatore, può manifestarsi come un colpo secco e forte oppure come un rombo basso e prolungato. Il fulmine causa un forte aumento di pressione e temperatura che a sua volta provoca la rapida espansione del canale ionizzato prodotto dal fulmine stesso: ...

Este artículo o sección necesita referencias que aparezcan en una publicación acreditada. Busca fuentes: «Planeador» – noticias · libros · académico · imágenesEste aviso fue puesto el 24 de mayo de 2019. Para otros usos de este término, véase Planeador (desambiguación). PlaneadorTipo Aerodino sin motor de ala fijaDiseñado por Otto Lilienthal en 1877Primer vuelo 1891[editar datos en Wikidata] Planeador Grob Astir. Un velero planeador, o simplemente...

Основная статья: Футбольное поле Футбольные ворота Футбольные ворота — ворота, используемые при игре в футбол; состоят из двух вертикальных стоек (штанги), находящихся на равном расстоянии от угловых флагштоков (то есть ворота должны размещаться по центру линии ворот...

King of Kakheti Constantine IIKing of Kakheti (more...) Reign1722–1732PredecessorDavid II of KakhetiSuccessorTeimuraz II of KakhetiBornIsfahan, Safavid IranDiedDecember 28, 1732DynastyBagrationi dynastyFatherHeraclius I of KakhetiReligionIslam Constantine II (Georgian: კონსტანტინე II) (died December 28, 1732), also known as Mahmād Qulī Khān (მაჰმად ყული-ხანი) in Iran, was a king (mepe) of Kakheti in eastern Georgia of the Bagrationi d...
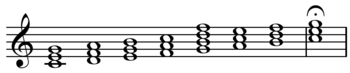
Chordal accompaniment to a line or melody This article is about harmonization in music. For other uses, see Harmonization (disambiguation). Two harmonizations of Yankee DoodleOne harmonization[1] Playⓘ.Another harmonization Playⓘ. Harmonized C major scale Playⓘ: I, ii, iii, IV, V7, vi, viio. In music, harmonization is the chordal accompaniment to a line or melody: Using chords and melodies together, making harmony by stacking scale tones as triads.[2] A harmonized scale ...

American professional society for medical doctors This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Pennsylvania Medical Society – news · newspapers · books · scholar · JSTOR (March 2009) (Learn how and when to remove this message) Pennsylvania Medical SocietyFormation1848FounderSamuel Humes, MDTypeProfessiona...






