Соответствие Галуа
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Ante Vokić Menteri Angkatan Bersenjata Negara Independen KroasiaMasa jabatan29 Januari 1944 – 8 Agustus 1944Perdana MenteriNikola Mandić PendahuluMiroslav NavratilPenggantiNikola SteinflMenteri Perhubungan Negara Independen KroasiaMasa ja...

Jessie MullerMuller in 2013LahirJessica Ruth Muller20 Februari 1983 (umur 41)Evanston, IllinoisPekerjaanAktris/Penyanyi Jessica Ruth Jessie Muller (lahir 20 Februari 1983)[1] adalah seorang aktris dan penyanyi. Dia memulai kariernya di Chicago dan memenangkan Joseph Jefferson Award pada tahun 2008 untuk perannya sebagai Carrie Pipperidge dalam Carousel. Pada tahun 2011, ia mempindahkan bakatnya ke New York City untuk membintangi revival Broadway dari On a Clear Day You Can See F...

Untuk tokoh Alkitab yang menjadi nama dari kitab ini, lihat Ayub (tokoh Alkitab). Untuk kegunaan lain, lihat Ayub (disambiguasi). Yosua 1:1 pada Kodeks Aleppo Perjanjian Lama (Kristen) Taurat Kejadian Keluaran Imamat Bilangan Ulangan Sejarah Yosua Hakim-hakim Rut 1 Samuel 2 Samuel 1 Raja-raja 2 Raja-raja 1 Tawarikh 2 Tawarikh Ezra Nehemia Ester Puisi Ayub Mazmur Amsal Pengkhotbah Kidung Agung Kenabian Besar Yesaya Yeremia Ratapan Yehezkiel Daniel Kecil Hosea Yoël Amos Obaja Yunus Mikha Nahum...
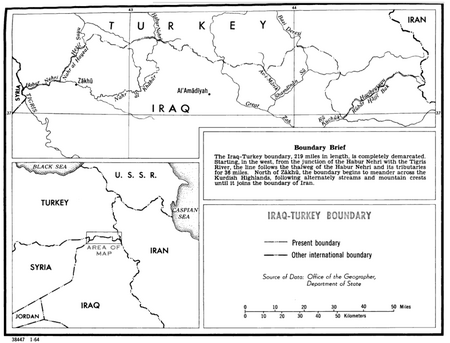
International border Between the Republic Of Turkey And The Republic Of Iraq Iraq-Turkey borderالحدود العراقية التركيةIrak–Türkiye sınırıCharacteristicsEntities Iraq TurkeyLength378 km (235 mi)[1] Map of the Iraq–Turkey border The Iraq–Turkey border (Kurdish: Sînorê Îraqê–Tirkiye, Arabic: الحدود العراقية التركية, romanized: alhudud aleiraqiat alturkia, Turkish: Irak–Türkiye sınırı) is 367 km...

Dev AnandPenyambutan Dev Anand oleh Perhimpunan Indo-AmerikaLahirDharam Devdutt Pishorimal Anand(1923-09-26)26 September 1923Shakargarh, Wilayah Punjab, India BritaniaMeninggal3 Desember 2011(2011-12-03) (umur 88)London, InggrisTempat tinggalMumbai, Maharashtra, IndiaKebangsaanIndiaNama lainDev SahaabPekerjaanAktor, produser, sutradara, pendiri Navketan Films (1949)Tahun aktif1946–2011Suami/istriKalpana Kartik (1954–2011 kematiannya)AnakSuneil AnandDevina AnandTanda tangan...

Pertempuran UjiBagian dari Perang GenpeiTanggalJuni 23, 1180LokasiUji, KyotoHasil Kemenangan Klan Taira, komandan Minamoto dan Pangeran Mochihito tewasPihak terlibat Klan Minamoto Klan TairaTokoh dan pemimpin Minamoto no Yorimasa Taira no TomomoriTaira no ShigehiraTemplat:Campaignbox Genpei War Pada awal 1180, Pangeran Mochihito, dari Klan Minamoto penerus tahta Kekaisaran, dikejar oleh pasukan Taira ke Mii-dera, sebuah kuil di luar Kyoto. Karena campur tangan dengan seorang biksu Mii-dera de...

العلاقات الأوزبكستانية الجورجية أوزبكستان جورجيا أوزبكستان جورجيا تعديل مصدري - تعديل العلاقات الأوزبكستانية الجورجية هي العلاقات الثنائية التي تجمع بين أوزبكستان وجورجيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدول�...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Rank comparison chart of Non-commissioned officer and enlisted ranks for navies of Anglophone states. Officers Rank group Senior NCOs Junior NCOs Enlisted Antigua and Barbuda Coast Guard[1]vte Master chief petty officer class 1 Master chief petty officer class 2 Chief petty officer Petty officer Leading seaman Able seaman Royal Australian Navy[2]vte Warrant Officer of the Navy Warrant officer Chief petty officer Petty officer Leading seaman Able seaman Seaman ...

Questa voce o sezione sull'argomento competizioni calcistiche non è ancora formattata secondo gli standard. Commento: Molte pagine di campionati regionali come queste vanno corrette con il nuovo modello di voce perché questa pagina è stata realizzata con modelli vecchi ed è obsoleta.In questa pagina sono da correggere:->le squadre partecipanti, con la tabellina in cui non è più possibile linkare le squadre non enciclopediche alle città, la città va scritta nella riga inferior...

Highest mountain in Turkey This article is about the place in Turkey. For other uses, see Mount Ararat (disambiguation). Not to be confused with Mount Arayat, Mount Arafat, or Mount Aragats. Mount Ararat Little Ararat (left) and Greater Ararat (right); View from Yerevan, ArmeniaHighest pointElevation5,137 m (16,854 ft)See Elevation sectionProminence3,611 m (11,847 ft)[1]Ranked 48thIsolation379.29 km (235.68 mi) ListingCountry high pointUltraVolc...

Disambiguazione – Se stai cercando il pittore cinquecentesco soprannominato Il Riccio, vedi Bartolomeo Neroni. Artista anonimo, medaglia di Andrea Briosco detto il Riccio, 1532 circa. Il Riccio, Satiro con calamaio, Metropolitan Museum Andrea Briosco, detto il Riccio e Crispo (Crispus) per la sua capigliatura folta e riccia (Trento, 1º aprile 1470 – Padova, 8 luglio 1532), è stato uno scultore italiano.[1] Indice 1 Biografia 2 Note 3 Bibliografia 4 Altri progetti 5 Collegamenti...

Голубянки Самец голубянки икар Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ПервичноротыеБез ранга:ЛиняющиеБез ранга:PanarthropodaТип:ЧленистоногиеПодтип:ТрахейнодышащиеНадкласс:ШестиногиеКласс...

Voce principale: Associazione Calcio Milan. Nereo Rocco (a sinistra) e Carlo Ancelotti (a destra) sono i due allenatori con più presenze e vittorie in assoluto nella storia del club. Qui di seguito sono riportati gli allenatori dell'Associazione Calcio Milan, società calcistica italiana per azioni con sede a Milano. Indice 1 Storia 2 Elenco cronologico degli allenatori 3 Statistiche 4 Titoli vinti 5 Record 5.1 Presenze in partite ufficiali 5.2 Vittorie in partite ufficiali 6 Riconoscimenti...

Den här artikeln behöver källhänvisningar för att kunna verifieras. (2023-08) Åtgärda genom att lägga till pålitliga källor (gärna som fotnoter). Uppgifter utan källhänvisning kan ifrågasättas och tas bort utan att det behöver diskuteras på diskussionssidan. Sana Duri är en årlig musikfestival i Göteborg. Den grundades år 2021 av festivalarrangören All Things Live i samarbete med Shuffle Group. På festivalen spelas mestadels hardstyle samt närbesläktade genrer som ha...

Il massacro di ScioAutoreEugène Delacroix Data1824 Tecnicaolio su tela Dimensioni417×354 cm UbicazioneMuseo del Louvre, Parigi Il massacro di Scio è un dipinto a olio su tela (417x354 cm) del pittore francese Eugène Delacroix, realizzato nel 1824 e conservato al museo del Louvre di Parigi. Indice 1 Storia 2 Descrizione 3 Note 4 Altri progetti 5 Collegamenti esterni Storia Eugène Delacroix, Studio di una testa di una donna anziana (1824); olio su tela, Musée des Beaux-Arts, Orléans...

ابن طيفور معلومات شخصية الميلاد سنة 819 بغداد الوفاة أغسطس 893 (73–74 سنة) بغداد مواطنة الدولة العباسية الحياة العملية المهنة لغوي، وشاعر، ومؤرخ، وجغرافي، وكاتب اللغات الفارسية، والعربية مؤلف:ابن طيفور - ويكي مصدر تعديل مصدري...

Para otros usos de este término, véase Montaje (desambiguación). Mesa de montaje convencional. El montaje o edición audiovisual es el proceso consistente en unir trozos de película para crear distintas secuencias, generalmente siguiendo un guion cinematográfico o idea del director de cine que termina en una producción final. En vídeo la palabra equivalente es edición, asegurarse de que cada uno de los detalles necesarios para una puesta en escena estén bien. Ya que de cada escena s...

Cognitive process to choose a course of action or belief This article is about decision-making as analyzed in psychology. For a broader discipline, see Decision theory. For decision-making in groups, see Group decision-making. Sample flowchart representing a decision process when confronted with a lamp that fails to light In psychology, decision-making (also spelled decision making and decisionmaking) is regarded as the cognitive process resulting in the selection of a belief or a course of a...

中国人民武装警察部队广东省总队中国人民武装警察部队旗存在時期1996年至今國家或地區 中华人民共和国種類武警内卫部队省级总队功能维护国家政治安全和社会稳定直屬武警总部[1]駐軍/總部广东省广州市專用顏色 橄榄绿指挥官司令员赵继东 武警少将政治委员王亞東 武警少将 中国人民武装警察部队广东省总队,简称武警广东省总队,是中国人民武装警察�...


























































