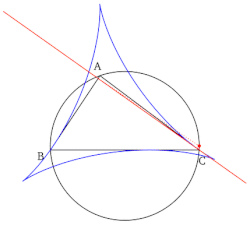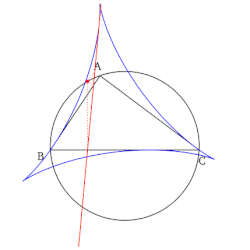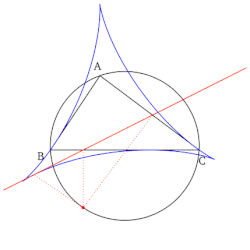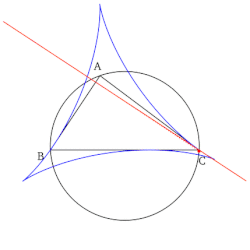
Прямая Симсона
|
Read other articles:

مقاطعة البندقية علم شعار الإحداثيات 45°27′N 12°24′E / 45.45°N 12.4°E / 45.45; 12.4 تاريخ التأسيس 23 ديسمبر 1866 تقسيم إداري البلد إيطاليا[1] التقسيم الأعلى فِنيتة العاصمة البندقية تاريخ الإلغاء 31 أغسطس 2015 التقسيمات الإدارية أنونيه فينيت...

География Узбекистана Часть света Азия Регион Средняя Азия Координаты 41°00 с. ш., 64°00 в. д. Площадь 56-я в мире 448 900 км² вода: 10 % суша: 90 % Береговая линия 0 км Границы всего: 6221 кмАфганистан (137 км)Казахстан (2203 км)Кыргызстан (1099 км)Таджикистан (1161 км)Туркменистан (1621 км) Вы�...

Catholic religious order Order of Preachers redirects here. For the Anglican religious order, see Anglican Order of Preachers. Order of PreachersOrdo Praedicatorum (Latin)Coat of arms of the orderAbbreviationOPFormation1206 (for women)1215 (for men)December 22, 1216 (December 22, 1216) (of pontifical right)FounderDominic de GuzmánFounded atProuille, France (for women)Toulouse, France (for men)HeadquartersConvento Santa Sabina, Piazza Pietro d'Illiria 1, Rome, Italy[1]Member...
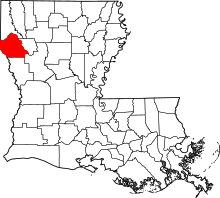
Location of DeSoto Parish in Louisiana This is a list of the National Register of Historic Places listings in DeSoto Parish, Louisiana. This is intended to be a complete list of the properties and districts on the National Register of Historic Places in DeSoto Parish, Louisiana, United States. The locations of National Register properties and districts for which the latitude and longitude coordinates are included below, may be seen in a map.[1] There are 28 properties and districts l...

Kereta api uap JaladaraKereta api uap Jaladara.IkhtisarJenisKereta api wisataStatusBeroperasiLokasiDaop 6 YogyakartaTerminusPurwosariSolo KotaOperasiDibukaca. 1920-2007PemilikPT Kereta Api IndonesiaOperatorKAI WisataPemerintah Kota SurakartaDepoPurwosari (PWS)RangkaianC 12 18 D 14 10Data teknisPanjang lintas6 kmLebar sepur1.067 mmKecepatan operasi20 km/jam C 12 18, lokomotif khas penarik KA Jaladara Kereta api uap Jaladara (Hanacaraka: ꦱꦼꦥꦸꦂꦏ꧀ꦭꦸꦛꦸꦏ꧀ꦗꦭꦢꦫ...

Kerusuhan KozaSeorang prajurit militer AS berdiri di dekat Volkswagen Karmann Ghia yang terbakar di Koza, beberapa jam setelah kerusuhan.Tanggal20 Desember 1970LokasiKoza, OkinawaPartisipanPenduduk Okinawa;prajurit AmerikaHasil56–60 prajurit Amerika terluka; 21 warga Okinawa ditangkap Situs kerusuhan sekitar 15 tahun sebelumnya, c. 1955. Kerusuhan Koza (コザ暴動code: ja is deprecated , Koza bōdō) adalah protes keras dan spontan terhadap kehadiran militer AS di Okinawa, yang terjadi pa...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (mai 2022). Si vous disposez d'ouvrages ou d'articles de référence ou si vous connaissez des sites web de qualité traitant du thème abordé ici, merci de compléter l'article en donnant les références utiles à sa vérifiabilité et en les liant à la section « Notes et références ». En pratique : Quelles sources sont attendues ? Comme...

لمعانٍ أخرى، طالع انتفاضة (توضيح). الانتفاضة هي حركة شعبية واسعة لمقاومة الاحتلال أو الظلم ، وقد اصطلح على تسمية الحركات الشعبية الفلسطينية المقاومة للاحتلال الإسرائيلي بالانتفاضة.[1][2] الانتفاضة الفلسطينية ينظر إلى تاريخ النضال الفلسطيني ضد الاحتلال الإس�...

Peta infrastruktur dan tata guna lahan di Komune Fouchécourt. = Kawasan perkotaan = Lahan subur = Padang rumput = Lahan pertanaman campuran = Hutan = Vegetasi perdu = Lahan basah = Anak sungaiFouchécourt merupakan sebuah komune di departemen Vosges yang terletak pada sebelah timur laut Prancis. Lihat pula Komune di departemen Vosges Referensi INSEE Diarsipkan 2007-11-24 di Wayback Machine. lbsKomune di departemen Vosges Les Ableuvenettes Ahév...

Untuk kegunaan lain, lihat Abdul Latief. Kolonel Inf.Abdul Latief Informasi pribadiLahir(1926-07-27)27 Juli 1926[1]Surabaya, Jawa TimurMeninggal6 April 2005(2005-04-06) (umur 78)Sebab kematianPenyakit paru-paru[1]Alma mater● KNIL (wamil) – 1942● Seinendan – 1943● SSKAD – 1957[1]Karier militerPihakIndonesiaMasa dinas1942–1965Pangkat KolonelNRP10685[1]SatuanInfanteriSunting kotak info • L • B Kolonel Inf. Abdul Latief (2...

Concept of non-human beings disguised as human For the first time Psyche sees the true form of her lover Eros; darkness had hidden his wings A human disguise (also human guise and sometimes human form)[1] is a concept in fantasy, folklore, mythology, religion, literature, iconography, and science fiction whereby non-human beings such as gods, angels, monsters, extraterrestrials, or robots are disguised to seem human.[2][3] Stories have depicted the deception as a means...

Genus of millipedes Julus Mating pair of Julus carpathicus Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Arthropoda Subphylum: Myriapoda Class: Diplopoda Order: Julida Family: Julidae Tribe: Julini Genus: JulusLinnaeus, 1758 Species[1] See text Julus (alternately written as Iulus) is a genus of millipedes in the family Julidae, containing the following species: Julus abbreviatus Mikan, 1834 Julus acriculus Karsch, 1881 Julus adensameri Verhoeff, 1897 Julus affi...

2024 war drama miniseries Masters of the AirGenreWar dramaCreated by John Shiban John Orloff Based onMasters of the Airby Donald L. MillerDeveloped byJohn OrloffDirected by Cary Joji Fukunaga Dee Rees Anna BodenRyan Fleck Tim Van Patten Starring Austin Butler Callum Turner Anthony Boyle Barry Keoghan Nikolai Kinski Stephen Campbell Moore Sawyer Spielberg Isabel May James Murray Nate Mann Kai Alexander Laurie Davidson Joanna Kulig Louis Hofmann Jamie Parker Bel Powley Sam Hazeldine Josiah Cros...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

Argentine swimmer Luis NicolaoNicola c. 1960Personal informationFull nameLuis Alberto Nicolao YanuzziNicknameNicoNationalityArgentineBorn (1944-06-28) June 28, 1944 (age 79)Buenos Aires, ArgentinaHeight1.82 m (6 ft 0 in)Weight74 kg (163 lb)SportSportSwimmingStrokesFreestyle, ButterflyClubAteneo de la JuventudCoachAlberto Profe Carranza Medal record Men's swimming Representing Argentina Pan American Games 1963 São Paulo 4x100 m medley 1963 São Paulo 2...

Article principal : 1907. Article connexe : Décès en 1907. Chronologies Données clés 1904 1905 1906 1907 1908 1909 1910Décennies :1870 1880 1890 1900 1910 1920 1930Siècles :XVIIIe XIXe XXe XXIe XXIIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, République centrafricaine, Comores, République du Cong...

Makam Michel Drach di Pemakaman Père-Lachaise, Paris (divisi 7) Michel Drach (Paris 18 Oktober 1930 – 15 Februari 1990) merupakan seorang sutradara Prancis, penulis, produser dan pemeran. Setelah belajar melukis di Académie des Beaux-Arts, ia terlibat dalam perfilman sebagai asisten sepupunya Jean-Pierre Melville.[1] Dia menyutradarai tiga film pendek dengan perusahaan produksinya Port Royal Films, termasuk Les Soliloques du pauvre (1951) dan Auditorium (1957), kemudian membuat de...

Music genre Alternative metalStylistic origins Heavy metal alternative rock Cultural originsMid-1980s, United StatesDerivative formsGrungeSubgenres Funk metal nu metal rap metal Fusion genres Neue Deutsche Härte[1] Regional scenesCaliforniaLocal scenesLos Angeles, California[2][3] Alternative metal (also known as alt-metal)[4] is a genre of heavy metal music that combines heavy metal with influences from alternative rock and other genres not normally associate...

Dorand AR Dorand AR.1 Tipo Avión de reconocimientoFabricante Section Technique de l'AéronautiquePrimer vuelo 1916Introducido 1917Usuario principal Fuerza Aérea FrancesaFuerza Expedicionaria EstadounidenseAviación Serbia[editar datos en Wikidata] El Dorand AR fue un avión biplano de observación francés de dos asientos de la Primera Guerra Mundial utilizado por la Fuerza Aérea Francesa, la Fuerza Expedicionaria Americana y, en menor medida, por la Aviación Serbia.[1][2...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Grimmiaceae Grimmia ovalis Klasifikasi ilmiah Kerajaan: Plantae Divisi: Bryophyta Kelas: Bryopsida Subkelas: Dicranidae Ordo: Grimmiales Famili: GrimmiaceaeArn.[1] Genera Lihat teks Grimmiaceae adalah famili lumut daun yang termasuk dalam ordo...