–ú–Ķ–ī–ł–į–Ĺ–į (—Ā—ā–į—ā–ł—Ā—ā–ł–ļ–į)
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Heiko Butscher Informasi pribadiTanggal lahir 28 Juli 1980 (umur 43)Tempat lahir Leutkirch, Jerman BaratTinggi 1,89 m (6 ft 2+1⁄2 in)Posisi bermain Bek tengahInformasi klubKlub saat ini VfL BochumNomor 5Karier junior SV Dietm...

Artikel ini perlu diwikifikasi agar memenuhi standar kualitas Wikipedia. Anda dapat memberikan bantuan berupa penambahan pranala dalam, atau dengan merapikan tata letak dari artikel ini. Untuk keterangan lebih lanjut, klik [tampil] di bagian kanan. Mengganti markah HTML dengan markah wiki bila dimungkinkan. Tambahkan pranala wiki. Bila dirasa perlu, buatlah pautan ke artikel wiki lainnya dengan cara menambahkan [[ dan ]] pada kata yang bersangkutan (lihat WP:LINK untuk keterangan lebih lanjut...

Kabupaten MadiunLambang Kabupaten MadiunPetahanaTontro Pahlawanto (Pj.)sejak 24 September 2023KediamanPendopo Bupati Madiun, CarubanDibentuk8 Juli 1568Pejabat pertamaPangeran TimoerSitus webmadiunkab.go.id Berikut adalah artikel tentang Daftar Bupati Madiun, provinsi Jawa Timur, Indonesia, dari masa ke masa dari tahun 1568. No Bupati Mulai menjabat Akhir menjabat Prd. Ket. Wakil Bupati 1 P. Timoer 1568 1586 1 ‚ÄĒ 2 R.A. Retno Djumilah 1586 1590 2 3 R.M. Rangsang 1590 1591 3 4 R.M. Sumeka...

ŔÖōĪŔÉō≤ ōßŔĄōīŔäōģ ōĻō®ōĮ ōßŔĄŔĄŔá ōßŔĄō≥ōßŔĄŔÖ ōßŔĄōęŔāōßŔĀŔä ōīōĻōßōĪ ŔÖōĪŔÉō≤ ōßŔĄōīŔäōģ ōĻō®ōĮ ōßŔĄŔĄŔá ōßŔĄō≥ōßŔĄŔÖ ōßŔĄōęŔāōßŔĀŔä ō•ō≠ōĮōßōęŔäōßō™ 29¬į20‚Ä≤38‚Ä≥N 48¬į02‚Ä≤29‚Ä≥E / 29.343917¬įN 48.041278¬įE / 29.343917; 48.041278 ŔÖōĻŔĄŔąŔÖōßō™ ōĻōßŔÖō© ŔÜŔąōĻ ōßŔĄŔÖō®ŔÜŔČ ŔÖō™ō≠ŔĀōĆ ō™ōßōĪŔäōģōĆ ŔÖōĻōßōĶōĪ ōßŔĄŔÖŔąŔāōĻ ōßŔĄō≥ōßŔĄŔÖŔäō© ōßŔĄŔāōĪŔäō© ō£Ŕą ōßŔĄŔÖōĮŔäŔÜō© ŔÖŔÜō∑Ŕāō© ōßŔĄōīŔźŔĎōĻŔźō® ōßŔĄōĮŔąŔĄō© ōĮŔąŔĄō© ōßŔĄŔÉŔąŔäō™ ō≥ŔÜō© ōßŔĄō™ō£ō≥ÔŅĹ...

Harold Brown Menteri Pertahanan Amerika Serikat ke-14Masa jabatan21 Januari 1977 ‚Äď 20 Januari 1981PresidenJimmy Carter PendahuluDonald RumsfeldPenggantiCaspar WeinbergerPresiden Institut Teknologi California ke-3Masa jabatan1969‚Äď1977 PendahuluLee Alvin DuBridgePenggantiRobert F. Christy (pelaksana tugas)Menteri Angkatan Udara Amerika Serikat ke-8Masa jabatan1 Oktober 1965 ‚Äď 15 Februari 1969PresidenLyndon B. Johnson PendahuluEugene M. ZuckertPenggantiRobert SeamansDirek...

Explore Scientific LLCCompany typeLLCIndustryImaging/ManufacturingFoundedLaguna Hills, California (2008)HeadquartersSpringdale, ArkansasProductsTelescopes, spotting scopes, binoculars, eyepieces and microscopesOwnerJourneyNorth Inc. (2014‚Äďpresent)Websitewww.explorescientificusa.com Explore Scientific is a company founded by former Meade Instruments Vice President of Brand Community Scott W. Roberts in 2008. Headquartered in Springdale, Arkansas, the company designs and manufactures telescop...

American children's religious television series This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Gerbert TV series ‚Äď news ¬∑ newspapers ¬∑ books ¬∑ scholar ¬∑ JSTOR (July 2016) (Learn how and when to remove this template message) GerbertTitle cardCreated byAndy HolmesCountry of originUnited StatesNo. of seas...

Hong Kong TV series or program With or Without YouOfficial posterAlso known asTung Po's Family AffairsśĚĪŚĚ°Śģ∂šļčGenrePeriod drama, historical fiction, ComedyCreated byHong Kong Television Broadcasts LimitedWritten byAu Yin Yuan, Ngai Hong YeeStarringBobby Au-YeungJoey MengVincent WongJacqueline WongAlice ChanHarriet YeungTheme music composerJin NakamuraOpening themeI Am Not Good Enough śąĎšłćŚ§†Ś•Ĺ by Linda ChungCountry of originHong KongOriginal languagesCantoneseMandarinNo. of episodes30...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne cite pas suffisamment ses sources (juin 2019). Si vous disposez d'ouvrages ou d'articles de r√©f√©rence ou si vous connaissez des sites web de qualit√© traitant du th√®me abord√© ici, merci de compl√©ter l'article en donnant les r√©f√©rences utiles √† sa v√©rifiabilit√© et en les liant √† la section ¬ę Notes et r√©f√©rences ¬Ľ. En pratique : Quelles sources sont attendues ? Comm...

Questa voce o sezione sull'argomento nobili austriaci non cita le fonti necessarie o quelle presenti sono insufficienti. Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Maria Giovanna Gabriella d'Asburgo-LorenaRitratto dell'arciduchessa Maria Giovanna Gabriella d'Asburgo-LorenaArciduchessa d'Austria Nome completoMaria Johanna Gabriela Josepha Antonia TrattamentoSua Altezza Imperiale e Reale Altri titoliPrincipessa ...

American actress (born 1963) Not to be confused with late male actor Anthony Johnson, who went as A.J. Johnson. Adrienne-Joi JohnsonJohnson in 2020Born (1963-01-02) January 2, 1963 (age 61)Orange, New Jersey, U.S.Other namesA.J. JohnsonAlma materSpelman CollegeOccupationsActressdancerfitness trainerlife coachmodelYears active1987–presentWebsitewww.theajzone.com Adrienne-Joi Johnson (born January 2, 1963),[1] also known as A.J. Johnson, is an American actress,...

Leishmania donovani L. donovani pada sel sumsum tulangTaksonomiSuperdomainBiotaSuperkerajaanEukaryotaKerajaanProtozoaSubkerajaanEozoaInfrakerajaanEuglenozoaFilumEuglenozoaSubfilumGlycomonadaKelasKinetoplasteaSubkelasMetakinetoplastinaOrdoTrypanosomatidaFamiliTrypanosomatidaeSubfamiliLeishmaniinaeGenusLeishmaniaSpesiesLeishmania donovani Laveran dan Mesnil, 1903 lbs Leishmania donovani adalah parasit intraseluler yang termasuk genus Leishmania, kelompok hemoflagelata penyebab leishmaniasis. Pa...
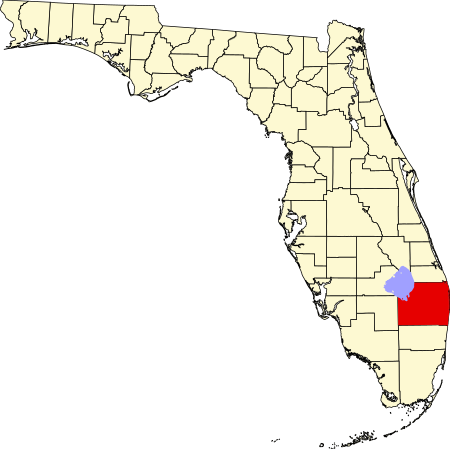
County in Florida, United States CountyPalm Beach CountyCounty Palm Beach FlagSealPalm Beach CountyLocation within the United StatesCoordinates: 26¬į43‚Ä≤N 80¬į03‚Ä≤W / 26.71¬įN 80.05¬įW / 26.71; -80.05[1]FoundedApril 30, 1909County seatWest Palm BeachLargest cityWest Palm BeachArea ‚ÄĘ Total6,170 km2 (2,383 sq mi) ‚ÄĘ Land5,100 km2 (1,970 sq mi) ‚ÄĘ Water1,070 km2 (413 sq mi)Population&...

Ongoing COVID-19 viral pandemic in Manitoba, Canada COVID-19 pandemic in ManitobaDiseaseCOVID-19Virus strainSARS-CoV-2LocationManitoba, CanadaFirst outbreakWuhan, Hubei, ChinaIndex caseWinnipegArrival dateMarch 12, 2020(4 years and 3 months)Confirmed cases56,482Active cases1,022Recovered54309Deaths1,151Fatality rate2.08%Government websiteGovernment of Manitoba The COVID-19 pandemic in Manitoba is a viral pandemic of coronavirus disease 2019 (COVID-19), a novel infectious disease cau...

Overview about the Egyptian pyramid construction techniques The three main pyramids at Giza, together with subsidiary pyramids and the remains of other ancient structures Egyptian pyramid construction techniques are the controversial subject of many hypotheses. These techniques seem to have developed over time; later pyramids were not constructed in the same way as earlier ones. Most of the construction hypotheses are based on the belief that huge stones were carved from quarries with copper ...

ōßŔĄō∑ō®ŔäōĻō© ōĻōĮŔĄ ō®Ŕąōßō®ō© ō∑ō®ŔäōĻō© ōßŔĄō∑ō®ŔäōĻō© ō®ŔÖōĻŔÜōßŔáōß ōßŔĄōĻōßŔÖ .ō™ōĻŔÜŔä ōßŔĄōĻōßŔĄŔÖ ōßŔĄō∑ō®ŔäōĻŔä ō£Ŕą ōßŔĄōĻōßŔĄŔÖ ōßŔĄŔĀŔäō≤Ŕäōßō¶Ŕä ō£Ŕą ōßŔĄōĻōßŔĄŔÖ ōßŔĄŔÖōßōĮŔä. Ŕąō™ōīŔäōĪ ŔÉŔĄŔÖō© ōßŔĄō∑ō®ŔäōĻō© ō•ŔĄŔČ ōłōßŔáōĪō© ōßŔĄōĻōßŔĄŔÖ ōßŔĄŔĀŔäō≤Ŕäōßō¶Ŕäōõ ŔÉŔÖōß ō™ōīŔäōĪ ō•ŔĄŔČ ōßŔĄō≠Ŕäōßō© ōĻŔÖŔąŔÖŔčōß. ŔáŔą ŔÖōĶō∑ŔĄō≠ ōĻōßŔÖ ŔąōīōßŔÖŔĄ Ŕäō¨ŔÖōĻ ō®ŔäŔÜ ōĻōßŔĄŔÖ ōßŔĄŔÖōßōĮō© ŔąōßŔĄŔÉŔąŔÜ ōßŔĄŔĀŔäō≤Ŕäōßō¶Ŕä ŔąŔÖōłōßŔáōĪ ōßŔĄō≠Ŕäōßō© ōßŔĄŔÖōģō™ŔĄŔĀō© ōßŔĄō∑ō®...

XK140 „É™„āĘ„āĻ„āŅ„ā§„Éę Śģ§ŚÜÖ „āł„É£„ā¨„Éľ„ÉĽXK140ÔľąJaguar XK140 ԾȄĀĮ„ā§„āģ„É™„āĻ„ĀģŤá™ŚčēŤĽä„É°„Éľ„āę„Éľ„āł„É£„ā¨„Éľ„ĀĆ1954ŚĻī[1][2]„Āč„āČ1957ŚĻī„Āĺ„Āß[2]ÁĒüÁĒ£„Āó„Ā¶„ĀĄ„Āü„āĻ„ÉĚ„Éľ„ÉĄ„āę„Éľ„Āß„Āā„āč„Äā ś¶āŤ¶Ā 1954ŚĻī„Āģ„É≠„É≥„ÉČ„É≥„ÉĘ„Éľ„āŅ„Éľ„ā∑„Éß„Éľ„Āę„Éě„Éľ„āĮVII M„Ā®ŚźĆśôā„Āę„ÄĀXK120„ĀģŚĺĆÁ∂ôśĒĻŤČĮŚěč„Ā®„Āó„Ā¶ÁôļŤ°®„Āē„āĆ„Āü[2]„ÄāXK140„Ā®„ĀĄ„ĀÜŚźćŚČć„ĀĮśúÄťęėťÄüŚļ¶„ĀĆ140mphÔľąÁīĄ225km/hԾȄĀß„Āā„āč„Āď„Ā®„Āę„āą„āč„Äā Ś§ĖŤ¶≥„ĀĮXK120„Ā®šľľ„Ā¶„ĀĄ„āč[...

Men's 400 metre freestyle at the 2014 FINA World Swimming Championships (25 m)Dates5 December (heats and semifinals)6 December (final)Competitors80 from 63 nationsWinning time3:34.32Medalists P√©ter Bernek Hungary James Guy Great Britain Velimir Stjepanovińá Serbia← 20122016 → 2014 FINA World Swimming ChampionshipsFreestyle50 mmenwomen100 mmenwomen200 mmenwomen400 mmenwomen800 mwomen1500 mmenBa...

City in Missouri, United StatesMarshfield, MissouriCityCity of MarshfieldThe Webster County Courthouse in MarshfieldLocation of Marshfield, MissouriCoordinates: 37¬į20‚Ä≤23‚Ä≥N 92¬į54‚Ä≤26‚Ä≥W / 37.33972¬įN 92.90722¬įW / 37.33972; -92.90722CountryUnited StatesStateMissouriCountyWebsterFounded1855Incorporated1856Named forMarshfield, MassachusettsGovernment ‚ÄĘ MayorNatalie McNish ‚ÄĘ City AdministratorSam RostArea[1] ‚ÄĘ Total5.53&...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2023. Darwin Ramos BiografiKelahiran17 Desember 1994 Pasay Kematian23 September 2012 (17 tahun)Filipina Data pribadiAgamaKatolik Exaltation (en) 2019 - Pelayan Tuhan, ditunjuk oleh Paus Fransiskus (Vatikan) Tanggal perayaan23 September Darwin Ram...





