Квантовая схема
|
Read other articles:

Questa voce o sezione sull'argomento esploratori portoghesi non cita le fonti necessarie o quelle presenti sono insufficienti. Commento: note bibliografiche completamente assenti Puoi migliorare questa voce aggiungendo citazioni da fonti attendibili secondo le linee guida sull'uso delle fonti. Viaggio di Juan Rodríguez Cabrillo Tiponavale Parte diColonizzazione spagnola delle Americhe ObiettivoEsplorare Data di partenza27 giugno 1542 Luogo di partenzaAcapulco Tappe principaliSan Diego,...

Untuk grup musik Indonesia, lihat SHE Band. S.H.E pada tahun 2010 S.H.E adalah grup musik dari Taiwan dan terkenal di beberapa negara Asia seperti Tiongkok, Hong Kong, Taiwan, Malaysia, Filipina dan Singapura. S.H.E terdiri dari tiga penyanyi wanita yaitu: Selina Ren, Hebe Tian, dan Ella Chen. Mereka merupakan salah satu grup Mandopop yang paling terkenal di Asia. S.H.E mengeluarkan album pertamanya yang berjudul Girls Dormitory (Hanzi: 女生宿舍) pada 11 September 2001. Sejak album pe...

A gas-operated oven/stove combination This is a list of cooking appliances that are used for cooking foods. Cooking appliances Using a caramelizer A domestic deep fryer with a wire basket An electric food steamer A microwave oven A hot-air style home popcorn maker A pressure cooker An electric rice cooker Air fryer Bachelor griller Barbecue grill Beehive oven Brasero Brazier Bread machine Burjiko Butane torch Chapati maker Cheesemelter Chocolatera Chorkor oven Clome oven Comal (cookware) Com...

Not to be confused with Inner World.This article is about the album by Mahavishnu Orchestra. For the video game, see Inner Worlds (video game). 1976 studio album by Mahavishnu OrchestraInner WorldsStudio album by Mahavishnu OrchestraReleasedJanuary 1976 (1976-01)[1]RecordedJuly-August 1975StudioChâteau d'Hérouville, FranceGenreJazz fusionLength44:07LabelSonyProducerJohn McLaughlin with Dennis MacKayMahavishnu Orchestra chronology Visions of the Emerald Beyond(1975)...
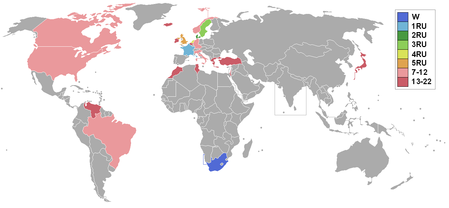
ملكة جمال العالم 1958 بينيلوبي كولين ، حاملة لقب مسابقة ملكة جمال العالم 1958بينيلوبي كولين ، حاملة لقب مسابقة ملكة جمال العالم 1958 تاريخ العرض 13 أكتوبر 1958 مقدم الحفل إيريك مورلي مكان مسرح لايسيوم، لندن، المملكة المتحدة مشاركين 22 ظهر لإول مرة البرازيل إنقطاع عن أسترالياالنمسا...

This article does not cite any sources. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Casa Pia – news · newspapers · books · scholar · JSTOR (September 2010) (Learn how and when to remove this message) The Castle of São Jorge, Casa Pia's first location The Casa Pia is a Portuguese institution founded by Maria I, known as A Pia (Mary the Pious), and organized by ...

Hungarian anthropologist, historian, ethnographer The native form of this personal name is Pócs Éva. This article uses Western name order when mentioning individuals. Éva Pócs, taken at the International Medieval Congress, 2014 Éva Pócs (born 1936[1]) is a Hungarian ethnographer and folklorist. Education and academic career Éva Pócs was born in 1936. She is the younger sister of botanist Tamás Pócs (born 1936). She began her career at the Néprajzi Múzeum where she was ...

لمعانٍ أخرى، طالع ماكس (توضيح). ماكسالشعارمعلومات عامةموقع الويب max.com (الإنجليزية) نوع الموقع خدمة بث الفيديو التأسيس 12 أبريل 2023 أهم الشخصياتالمالك وارنر برذرز. ديسكفري تعديل - تعديل مصدري - تعديل ويكي بيانات ماكس (بالإنجليزية: Max) أو كما كانت تعرف سابقاً إتش بي أو ماك...

American mathematician Bruce Sagan Bruce Eli Sagan (born March 29, 1954) is an American Professor of Mathematics at Michigan State University. He specializes in enumerative, algebraic, and topological combinatorics. He is also known as a musician, playing music from Scandinavia and the Balkans. Early life Sagan is the son of Eugene Benjamin Sagan and Arlene Kaufmann Sagan. He grew up in Berkeley, California. He started playing classical violin at a young age under the influence of his mother ...

American federal transportation program The Renewable Fuel Standard (RFS) is an American federal program that requires transportation fuel sold in the United States to contain a minimum volume of renewable fuels. It originated with the Energy Policy Act of 2005 and was expanded and extended by the Energy Independence and Security Act of 2007. Research published by the Government Accountability Office in November 2016 found the program unlikely to meet its goal of reducing greenhouse gas emiss...

Stage musical Chitty Chitty Bang BangPoster for original Broadway productionMusicRichard M. ShermanRobert B. ShermanLyricsRobert B. ShermanRichard M. ShermanBookJeremy SamsBasis Chitty Chitty Bang Bangby Roald DahlKen HughesRichard Maibaum Chitty-Chitty-Bang-Bangby Ian Fleming PremiereApril 16, 2002: London PalladiumProductions2002 West End2005 Broadway2005 national UK tour2007 Singapore2008/09 national US tour2009 UK & Ireland Tour2012/13 Australian national tour2014 Munich2015 - 2017 na...

American anti-war song from 1915 Cover page to the sheet music Alternate cover illustration I Didn't Raise My Boy to Be a Soldier I Didn't Raise My Boy to Be a Soldier sung by the Peerless Quartet in late 1914 Problems playing this file? See media help. I Didn't Raise My Boy to Be a Soldier is an American anti-war song that was influential within the pacifist movement that existed in the United States before it entered World War I.[1][2] It is one of the first anti-war songs.&...

Part of a series onAnarchism History Outline Schools of thought Feminist Green Primitivist Social ecology Total liberation Individualist Egoist Free-market Naturist Philosophical Mutualism Postcolonial African Black Queer Religious Christian Jewish Social Collectivist Parecon Communist Magonism Without adjectives Methodology Agorism Illegalism Insurrectionary Communization Expropriative Pacifist Platformism Especifismo Relationship Syndicalist Synthesis Theory Practice Anarchy Anarchist Blac...
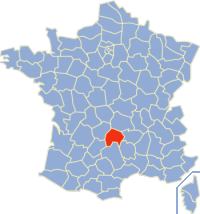
Untuk keju, silakan lihat Cantal (keju) Cantal (15) (dalam bahasa Occitan Cantal / Cantau / Chantal / Chantau) ialah sebuah département di Prancis, terletak di région Auvergne, dan mendapatkan namanya dari pegunungan Cantal. Letak Cantal di Prancis Sejarah Artikel utama: Sejarah Cantal Département ini diciptakan setelah Revolusi Prancis, pada 4 Maret 1790 dan diterapkan hukum pada 22 Desember 1789, dibentuk dari provinsi Auvergne, bekas provinsi yang kemudian bernama Haute-Auvergne. Politi...

Amtrak train station in Indiana For other stations with similar names, see Hammond station (disambiguation). Hammond–Whiting, INHammond–Whiting station building in 2010General informationLocation1135 South Calumet AvenueHammond, IndianaUnited StatesCoordinates41°41′28″N 87°30′24″W / 41.69111°N 87.50667°W / 41.69111; -87.50667Owned byAmtrakLine(s)NS Chicago LinePlatforms1Tracks4ConstructionParking10 short term, 103 long termAccessibleYesOther information...

SirHugh CourtenayKGHugh Courtenay from the Bruges Garter Book, 1430/1440, BL Stowe 594. The Courtenay arms are displayed on his tabard under his Garter robeBorn22 March 1327Diedafter Easter term 1348Noble familyCourtenaySpouse(s)Elizabeth de VereIssueHugh Courtenay (died 1374)FatherHugh Courtenay, 10th Earl of DevonMotherMargaret de Bohun Arms of Sir Hugh de Courtenay (d. circa 1348), KG: Or, three torteaux gules a label of three points azure each point charged with three annulets argent Sir ...

Unlimited or infinite benevolence Part of a series on theAttributes of God in Christianity Core attributes Omnibenevolence Omnipotence Omnipresence Omniscience Eternity Overarching attributes Aseity Oneness Perfection Trinity Miscellaneous Graciousness Holiness Immanence Immutability Impassibility Impeccability Incomprehensibility Incorporeality Kingship Mission Providence Righteousness Simplicity Sovereignty Transcendence Veracity Emotions expressed by God Jealousy Love Mercy Will Wrath vte ...

لمعانٍ أخرى، طالع صواري (توضيح). نادي الصواري السعودي الألوان السماوي و الأبيض تأسس عام 1980 م الملعب جازان السعودية البلد السعودية الدوري دوري الدرجة الثالثة السعودي الإدارة المالك الهيئة العامة للرياضة الطقم الأساسي الطقم الاحتياطي تعديل مصدري - تعديل نا�...

Coin of Anactorium Anactorium or Anaktorion (Ancient Greek: Ἀνακτόριον) was a town in ancient Acarnania, situated on the promontory on the Ambraciot Gulf. On entering the Ambraciot Gulf from the Ionian Sea it was the first town in Acarnania after Actium, from which it was distant 40 stadia, and which was in the territory of Anactorium. This town was for some time one of the most important places in this part of Greece. It was colonized jointly by the Corinthians and Corcyraeans; bu...

Municipality in Tartar, AzerbaijanDəmirçilərMunicipalityDəmirçilərShow map of AzerbaijanDəmirçilərShow map of Karabakh Economic RegionCoordinates: 40°25′36″N 46°53′45″E / 40.42667°N 46.89583°E / 40.42667; 46.89583Country AzerbaijanRayonTartarPopulation[citation needed] • Total1,078Time zoneUTC+4 (AZT) • Summer (DST)UTC+5 (AZT) Dəmirçilər (also, Damirchilyar and Demirchilyar) is a village and municipality in t...





















