Voievodul țiganilor
| |||||||||||||||||||||||||||||||||
Read other articles:

Election in Oklahoma Main article: 1968 United States presidential election 1968 United States presidential election in Oklahoma ← 1964 November 5, 1968 1972 → Nominee Richard Nixon Hubert Humphrey George Wallace Party Republican Democratic American Independent Home state New York[a] Minnesota Alabama Running mate Spiro Agnew Edmund Muskie Curtis LeMay Electoral vote 8 0 0 Popular vote 449,697 301,658 191,731 Percentage 47.68% 31.99% 20...

Voce principale: Athlītikī Enōsis Kōnstantinoupoleōs (pallacanestro). Athlītikī Enōsis KōnstantinoupoleōsStagione 2020-2021Sport pallacanestro Squadra AEK Atene Allenatore Īlias Papatheodōrou(fino al 10 aprile) Vaggelīs Angelou(dal 12 aprile) Assistenti Giōrgos Līmniatīs Dīmītrīs Menoudakos Savvas Symeonidis Presidente Makīs Angelopoulos Basket League4° (14-8) Play-off3° Champions LeaguePlay-Off Supercoppa greca4° Coppa di GreciaQuarti di finale Maggiori presenzeC...

追晉陸軍二級上將趙家驤將軍个人资料出生1910年 大清河南省衛輝府汲縣逝世1958年8月23日(1958歲—08—23)(47—48歲) † 中華民國福建省金門縣国籍 中華民國政党 中國國民黨获奖 青天白日勳章(追贈)军事背景效忠 中華民國服役 國民革命軍 中華民國陸軍服役时间1924年-1958年军衔 二級上將 (追晉)部队四十七師指挥東北剿匪總司令部參謀長陸軍�...

Bistagno commune di Italia Tempat Negara berdaulatItaliaRegion di ItaliaPiedmontProvinsi di ItaliaProvinsi Alessandria NegaraItalia Ibu kotaBistagno PendudukTotal1.748 (2023 )GeografiLuas wilayah17,59 km² [convert: unit tak dikenal]Ketinggian175 m Berbatasan denganCastelletto d'Erro Melazzo Monastero Bormida Montabone Ponti Rocchetta Palafea Sessame Terzo Montechiaro d'Acqui SejarahHari liburpatronal festival Santo pelindungYohanes Pembaptis Informasi tambahanKode pos15012 Zona wa...

Cortandonecomune Cortandone – VedutaPanorama LocalizzazioneStato Italia Regione Piemonte Provincia Asti AmministrazioneSindacoClaudio Stroppiana (lista civica Noi per Cortandone) dall'8-6-2009 (3º mandato dal 26-5-2019) TerritorioCoordinate44°57′36″N 8°03′34″E / 44.96°N 8.059444°E44.96; 8.059444 (Cortandone)Coordinate: 44°57′36″N 8°03′34″E / 44.96°N 8.059444°E44.96; 8.059444 (Cortandone) Altitudine21...

МифологияРитуально-мифологическийкомплекс Система ценностей Сакральное Миф Мономиф Теория основного мифа Ритуал Обряд Праздник Жречество Мифологическое сознание Магическое мышление Низшая мифология Модель мира Цикличность Сотворение мира Мировое яйцо Мифическое �...

هذه المقالة بحاجة لصندوق معلومات. فضلًا ساعد في تحسين هذه المقالة بإضافة صندوق معلومات مخصص إليها.Learn how and when to remove this message التنقيع هي عملية تشريب مواد صلبة في سائل (الماء عادة) وذلك لاستخراج طعماتها أو لتخفيف ذلك.[1] يُعدّ بعض الشاي للشرب عن طريق نقع أوراقه بالماء الساخن ل...

Irving and 8th Avenue9th Avenue and IrvingA westbound train at 9th Avenue and Irving in September 2019General informationLocationIrving Street at 8th Avenue (eastbound)9th Avenue at Irving Street (westbound)San Francisco, CaliforniaCoordinates37°45′51″N 122°27′59″W / 37.76404°N 122.46632°W / 37.76404; -122.46632Platforms2 side platformsTracks2Connections Muni: 44ConstructionAccessibleNoHistoryOpenedOctober 21, 1928 (1928-10-21)[1 ...

The list of shipwrecks in November 1939 includes ships sunk, foundered, grounded, or otherwise lost during November 1939. This is a dynamic list and may never be able to satisfy particular standards for completeness. You can help by adding missing items with reliable sources. November 1939 MonTueWedThuFriSatSun 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 Unknown date References 1 November List of shipwrecks: 1 November 1939 Ship State Description Mervyn &...

白玉刚(蒙古语:ᠪᠠᠢᠢᠤᠢᠭᠠᠩ;1965年8月—)。男,蒙古族,内蒙古达拉特旗人,中华人民共和国政治人物。北京大学中文系中文专业毕业,内蒙古农业大学经济管理学院农业经济专业硕士研究生课程班在职研究生学历。 生平 1984年9月,在北京大学中文系中文专业学习。1988年7月参加工作,任内蒙古自治区伊克昭盟计划委员会干事。1990年2月,任伊克昭盟行政公署干�...

Effort to map CJK characters in Unicode Unihan redirects here. For the historical period, see Chu–Han Contention. For other uses, see Unihan (disambiguation). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.F...

Brazilian musician (1929–2010) Johnny AlfJohnny AlfBackground informationBirth nameAlfredo José da SilvaBorn(1929-05-19)May 19, 1929Rio de JaneiroDiedMarch 4, 2010(2010-03-04) (aged 80)Santo André, BrazilOccupation(s)Musician, teacherMusical artist Alfredo José da Silva (May 19, 1929 – March 4, 2010), popularly known as Johnny Alf, was a Brazilian musician, sometimes known as the Father of Bossa Nova.[1] Alf was born in Vila Isabel, Rio de Janeiro, and began playing piano ...

Academic hospital in San Antonio,Texas, US UT Health San AntonioMottoDisciplina, Praesidium, CivitatisTypePublic academic health science centerEstablished1959Parent institutionUniversity of Texas SystemEndowment$781 million (FY 23)[1]PresidentRobert A. Hromas, MD, FACP (Acting/Interim)Academic staff2,400[1]Total staff8,500Students4,759Undergraduates3,656Postgraduates1,103LocationSan Antonio, Texas, United States29°30'28.2N 98°34'32.3WCampusUrban, 250 acres (100 ha)Websi...
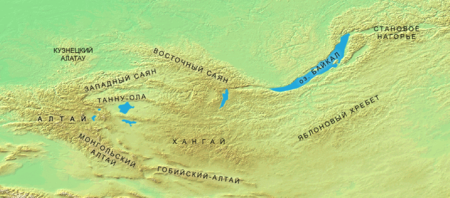
Южная Сибирь регион Страна Россия Западная и центральная части горной страны Ю́жная Сиби́рь — часть Сибири, выделяемая по различным основаниям. 1. По физико-географическим условиям Южная Сибирь, это: горная страна, протянувшаяся с запада на восток от Западно-Сибир�...

ستراثوري كاردوك الإحداثيات 42°54′39″N 81°31′59″W / 42.910833333333°N 81.533055555556°W / 42.910833333333; -81.533055555556 [1] [2] تاريخ التأسيس 1832 تقسيم إداري البلد كندا[3][4] عدد السكان عدد السكان 20867 (2016)[5] معلومات أخرى N7G رمز جيونيمز 6158028 الموقع ال...
この記事で示されている出典について、該当する記述が具体的にその文献の何ページあるいはどの章節にあるのか、特定が求められています。 ご存知の方は加筆をお願いします。(2020年5月) 難波一甫流なんばいっぽりゅう 画像をアップロード発生国 日本創始者 難波一甫斎久永派生流派 不遷流主要技術 捕手術、剣術、杖術、腰廻、捕縄術伝承地 広島県、岡山県テン�...

Military rank This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Colonel general – news · newspapers · books · scholar · JSTOR (July 2021) (Learn how and when to remove this message) Comparative military ranks Armies,air forces (non-Commonwealth) Navies, coast guards Air forces(Commonwealth system)Flag commissi...

Autochthonous group inhabiting the Aegan region according Greek mythology This article provides insufficient context for those unfamiliar with the subject. Please help improve the article by providing more context for the reader. (June 2016) (Learn how and when to remove this message) For other uses, see Minyan (disambiguation). In Greek mythology, the Minyans or Minyae (Greek: Μινύες, Minyes) were a group of legendary people who were the inhabitants of the city Orchomenus in Boeotia, a...

Millennium Prize Problem Flow visualization of a turbulent jet, made by laser-induced fluorescence. The jet exhibits a wide range of length scales, an important characteristic of turbulent flows. Millennium Prize Problems Birch and Swinnerton-Dyer conjecture Hodge conjecture Navier–Stokes existence and smoothness P versus NP problem Poincaré conjecture (solved) Riemann hypothesis Yang–Mills existence and mass gap vte The Navier–Stokes existence and smoothness problem concerns the math...

A hyperreal number that is equal to its own integer part In nonstandard analysis, a hyperinteger n is a hyperreal number that is equal to its own integer part. A hyperinteger may be either finite or infinite. A finite hyperinteger is an ordinary integer. An example of an infinite hyperinteger is given by the class of the sequence (1, 2, 3, ...) in the ultrapower construction of the hyperreals. Discussion The standard integer part function: ⌊ x ⌋ {\displaystyle \lfloor x\rfloor }...


