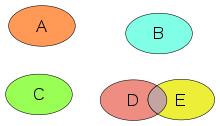
Reuniune (matematică)
|
Read other articles:

Kepangeranan AndorraPrincipat d'Andorra (Catalonia) Bendera Lambang Semboyan: Virtus Unita Fortior (Kekuatan bersatu lebih kuat)Lagu kebangsaan: El Gran Carlemany (Charlemagne yang Gagah) Ibu kota(dan kota terbesar)Andorra la Vella42°30′N 1°31′E / 42.500°N 1.517°E / 42.500; 1.517Bahasa resmiCataloniaKelompok etnik (2021[1]) 48,3% Andorra 24,8% Spanyol 11,2% Portugis 4,5% Prancis 1,4% Argentina 9,8% lainnya Agama (2020)[3] 90,8% Ke...

CoquimatlánKursi munisipal dan kotaCoquimatlan Lambang kebesaranCoquimatlánLetak di MeksikoKoordinat: 19°12′13.6″N 103°48′31″W / 19.203778°N 103.80861°W / 19.203778; -103.80861Koordinat: 19°12′13.6″N 103°48′31″W / 19.203778°N 103.80861°W / 19.203778; -103.80861Negara MeksikoNegara bagianColimaMunisipalitasCoquimatlánPopulasi (2010) • Munisipalitas19.385 • Seat13.358 Coquimatlán adalah...

العلاقات البرتغالية اليمنية البرتغال اليمن البرتغال اليمن تعديل مصدري - تعديل العلاقات البرتغالية اليمنية هي العلاقات الثنائية التي تجمع بين البرتغال واليمن.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدولتين: وجه المقارن...

Semangkuk corn flakes dengan susu. Sereal sarapan (atau sereal) adalah makanan yang umumnya dimakan sebagai sarapan. Makanan ini umumnya dimakan dingin, dan dimakan bersama susu, air atau yoghurt, atau dimakan langsung. Beberapa jenis sereal, seperti havermut, dapat dipanaskan sehingga menjadi seperti bubur. Sereal umumnya dipromosikan sebagai penunjang kesehatan dengan memakan sarapan berserat tinggi. Sereal juga mengandung vitamin dan mineral. Namun ada beberapa sereal yang mengandung kadar...

Greek national poet This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Dionysios Solomos – news · newspapers · books · scholar · JSTOR (May 2021) (Learn how and when to remove this template message) Dionysios SolomosNative nameΔιονύσιος ΣολωμόςBorn(1798-04-08)8 April 1798Zakynthos, Département ...

Pour les articles homonymes, voir Stasi (homonymie). Bernard Stasi Fonctions Médiateur de la République 2 avril 1998 – 13 avril 2004(6 ans et 11 jours) Prédécesseur Jacques Pelletier Successeur Jean-Paul Delevoye Député européen 19 juillet 1994 – 24 avril 1998(3 ans, 8 mois et 25 jours) Élection 12 juin 1994 Député français 23 juin 1988 – 1er avril 1993(4 ans, 9 mois et 9 jours) Élection 12 juin 1988 Circonscription 6e de la Marne Lé...

Call of Duty: Modern Warfare 2 adalah permainan video penembak orang pertama yang dikembangkan oleh Infinity Ward dan diterbitkan oleh Activision. Dirilis di seluruh dunia pada 10 November 2009, itu menimbulkan beberapa kontroversi. Salah satu kontroversi yang paling bisa dibilang terkenal ini ditemukan di level keempat permainan, No Russian, di mana pemain mengontrol agen CIA yang menyamar yang berpartisipasi dalam penembakan massal di bandara Moskow untuk mendapatkan kepercayaan dari kelomp...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Asabri – berita · surat kabar · buku · cendekiawan · JSTOR PT Asabri (Persero)Kantor pusat Asabri di JakartaSebelumnyaPerusahaan Umum Asuransi Sosial Angkatan Bersenjata Republik IndonesiaJenisPerusahaan...

Broadway theater in Manhattan, New York Sam S. Shubert Theatre redirects here. For the theater in Boston, see Shubert Theatre (Boston). Shubert TheatreAddress225 West 44th StreetManhattan, New York CityUnited StatesCoordinates40°45′29″N 73°59′14″W / 40.75806°N 73.98722°W / 40.75806; -73.98722Public transitSubway: Times Square–42nd Street/Port Authority Bus TerminalOwnerShubert and Booth Theatre, LLCOperatorThe Shubert OrganizationTypeBroadwayCapacity1,502...

Portuguese writer (1800–1875) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: António Feliciano de Castilho – news · newspapers · books · scholar · JSTOR (June 2023) (Learn how and when to remove this message) António Feliciano de CastilhoBorn28 January 1800 (1800-01-28)Lisbon, PortugalDied18 June 1...

Akmal TaherLahir27 Juli 1955 (umur 68)Jakarta, IndonesiaKebangsaanIndonesiaPekerjaan- Dirut RSCM, Jakarta- Ketua Ikatan Ahli Urologi Indonesia.Orang tuaTaher dan Rosnalia Akmal Taher (lahir 27 Juli 1955) adalah seorang dokter ahli bedah asal Indonesia. Ia pernah menjabat sebagai direktur utama Rumah Sakit Dr. Cipto Mangunkusumo, Jakarta dan Ketua Ikatan Ahli Urologi Indonesia. Akmal merupakan pemilik hak paten use of inhibitor of phosphodiesterase IV di Jerman, Amerika Serikat, Kanada, ...

Katamachi Station潟町駅Katamachi Station in July 2015Lokasi539-3 Katamachi, Ogata-ku, Jōetsu-shi, Niigata-ken 949-3103JapanKoordinat37°14′04″N 138°20′23″E / 37.2344°N 138.3397°E / 37.2344; 138.3397Koordinat: 37°14′04″N 138°20′23″E / 37.2344°N 138.3397°E / 37.2344; 138.3397Operator JR EastJalur■ Shin'etsu Main LineJumlah peron2 side platformsJumlah jalur2Informasi lainStatusUnstaffedSitus webwww.jreast.co.jp/estation...

Pour les articles homonymes, voir Hauteville. Hauteville-sur-Mer La digue de Hauteville-sur-Mer Plage, promenade longue de 1,7 km. Administration Pays France Région Normandie Département Manche Arrondissement Coutances Intercommunalité Communauté de communes Coutances Mer et Bocage Maire Mandat Jean-René Binet (LR) 2020-2026 Code postal 50590 Code commune 50231 Démographie Gentilé Hautais Populationmunicipale 700 hab. (2021 ) Densité 211 hab./km2 Géographie Coordonné...

UK Parliament constituency in England since 1950 BolsoverCounty constituencyfor the House of CommonsBoundary of Bolsover in Derbyshire for the 2010 general electionLocation of Derbyshire within EnglandCountyDerbyshirePopulation94,473 (2011 census)[1]Electorate72,162 (December 2010)[2]Major settlementsBolsover, Shirebrook, Clowne, South NormantonCurrent constituencyCreated1950Member of ParliamentMark Fletcher (Conservative)SeatsOneCreated fromClay Cross and North East Derby...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

General and politician of the First French Empire (1753–1815) For the American privateer named after him, see Prince de Neufchatel. Marshal of the EmpireLouis-Alexandre BerthierPrince of Neuchâtel and Valangin, Prince of WagramPortrait by Jacques Pajou, 1808Minister of WarIn office11 November 1799 – 2 April 1800Preceded byEdmond Louis Alexis Dubois-CrancéSucceeded byLazare CarnotIn office8 October 1800 – 19 August 1807Preceded byLazare CarnotSucceeded byHenri Guillaume Clarke, Duke of...

National park site The National Park System is well endowed to commemorate Hispanic contributions to American society. Some 20 national parklands represent Hispanic heritage in the United States. Some sites remotely display Hispanic contributions to American culture.[1] The National Park System not only preserves the history and contributions of Hispanic Americans, it is also a part of the nation's history. Over the years, the National Park Service has reflected the nation's social hi...

2010 novel by Eric Flint 1635: The Eastern Front First edition coverAuthorEric FlintCover artistTom KiddLanguageEnglishSeries1632 seriesGenreAlternate History/Science fictionPublisherBaen BooksPublication dateOctober 5, 2010Publication placeUnited StatesMedia typePrint (hardback)Pages369 p.ISBN978-1-4391-3389-7OCLC555638250Dewey Decimal813.6LC ClassPS3556.L548 A61866 2010Preceded by1635: The Tangled Web Followed by1636: The Saxon Uprising 1635: The Eastern ...

Pour les articles homonymes, voir La Chapelle. La Chapelle-Pouilloux L'église Saint-Junien de La Chapelle-Pouilloux. Blason Administration Pays France Région Nouvelle-Aquitaine Département Deux-Sèvres Arrondissement Niort Intercommunalité Communauté de communes Mellois en Poitou Maire Mandat Marie-Emmanuelle Saintier 2020-2026 Code postal 79190 Code commune 79074 Démographie Populationmunicipale 174 hab. (2021 ) Densité 22 hab./km2 Géographie Coordonnées 46° 08′&#...