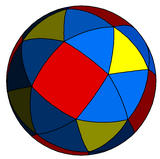
Cub snub
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Artikel ini membutuhkan rujukan tambahan agar kualitasnya dapat dipastikan. Mohon bantu kami mengembangkan artikel ini dengan cara menambahkan rujukan ke sumber tepercaya. Pernyataan tak bersumber bisa saja dipertentangkan dan dihapus.Cari sumber: Branchiopoda – berita · surat kabar · buku · cendekiawan · JSTOR Artikel ini bukan mengenai Brachiopoda. BranchiopodaRentang fosil: Upper Cambrian–Recent PreЄ Є O S D C P T J K Pg N Triops, (Notostraca: T...

Kelinci Paskah adalah makhluk fiktif yang digambarkan sebagai seekor kelinci antropomorfis. Menurut legenda, kelinci Paskah membawa keranjang yang penuh berisi telur, permen, dan mainan yang bewarna-warni ke rumah anak-anak pada malam Paskah. Kelinci Paskah itu akan menaruh keranjang tersebut di suatu tempat atau menyembunyikannya di dalam rumah anak itu agar sang anak keesokan paginya mencarinya. Kelinci Paskah memiliki kemiripan-kemiripan dengan Sinterklas yang membawa hadiah untuk anak-ana...

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Maio de 2012) Parte da série sobre EducaçãoEvolução acadêmica Educação infantil Infantário / Creche / Jardim de infância Educação básica Ensino primário / Ensino fundamental Ensino secundário / Ensino médio Ensino profissio...

Stadion Gelora Madura Ratu Pamelingan Informasi stadionPemilikPemkab PamekasanLokasiLokasiTlanakan, Pamekasan, Jawa TimurKoordinat7°11′40″S 113°28′45″E / 7.1943648°S 113.4790638°E / -7.1943648; 113.4790638KonstruksiDibuka18 November 2016[1]Direnovasi2017[2]Data teknisPermukaanRumput Zoysia matrellaKapasitas13,500 - 14,000PemakaiMadura United FCPamekasan FCPersepam Madura UtamaSunting kotak info • L • BBantuan penggunaan templat...

Artikel ini tentang tahun 1879. 1879MileniumMilenium ke-2AbadAbad ke-18Abad ke-19 Abad ke-20Dasawarsa 1850-an1860-an1870-an1880-an1890-anTahun1876187718781879188018811882 1879 (MDCCCLXXIX) adalah tahun biasa yang diawali hari Rabu dalam kalender Gregorian dan tahun biasa yang diawali hari Senin dalam kalender Julian, tahun ke-1879 dalam sebutan Masehi (CE) dan Anno Domini (AD), tahun ke-879 pada Milenium ke-2, tahun ke-79 pada Abad ke-19, dan tahun ke- 10 dan terakhir pada dekade 18...

Disambiguazione – Lingua rutena rimanda qui. Se stai cercando altri significati, vedi Lingua rutena (disambigua). Russino, RutenoРусиньскый (Rusin'skyj)Parlato in Ucraina Serbia Slovenia Slovacchia Regioni Voivodina LocutoriTotale614.200 Altre informazioniScritturaalfabeto cirillico TipoSVO TassonomiaFilogenesiLingue indoeuropee Lingue slave Lingue slave orientali Lingua russina Statuto ufficialeUfficiale in Voivodina (...

Il mio nome è ThomasTerence Hill in una scena del filmLingua originaleitaliano Paese di produzioneItalia Anno2018 Durata96 min Generedrammatico RegiaTerence Hill SoggettoTerence Hill, Luisa Tonon SceneggiaturaTerence Hill, Luisa Tonon ProduttoreJess Hill Produttore esecutivoAnselmo Parrinello, Paolo Luvisotti Casa di produzionePaloma4 srl, Vivi Film Distribuzione in italianoLux Vide FotografiaRoberta Allegrini MontaggioLuca Benedetti Effetti specialiAlessio Pericò, Giovanni Ermes Vincenti M...

U.S. governor election 1820 Delaware gubernatorial special election ← 1819 October 3, 1820 1822 (special) → Nominee John Collins Jesse Green Party Democratic-Republican Federalist Popular vote 3,970 3,520 Percentage 53.00% 47.00% Governor before election Jacob Stout Federalist Elected Governor John Collins Democratic-Republican Elections in Delaware Federal government Presidential elections 1788-89 1792 1796 1800 1804 1808 1812 1816 1820 1824 1828 1832 1836 1...

Italian businessman Francesco Gaetano CaltagironeCaltagirone with Giorgio Napolitano, President of the Italian RepublicBorn (1943-03-02) 2 March 1943 (age 81)[1]Rome, ItalyOther namesFrancesco Caltagirone, Franco CaltagironeOccupationBusinessmanKnown forOwns more than 50% of Caltagirone S.p.A.[2]SpouseLuisa FarinonChildren3 Francesco Gaetano Caltagirone (Italian pronunciation: [franˈtʃesko ɡa.eˈtaːno kaltadʒiˈroːne]; born 2 March 1943) is an Ital...

Experimental hypersonic glide vehicle Hypersonic Technology Vehicle HTV-2 reentry (artist's impression) Hypersonic Technology Vehicle 2 (HTV-2) is an experimental hypersonic glide vehicle developed as part of the DARPA Falcon Project designed to fly in the Mach 20 range.[1][2][3][4] It is a test bed for technologies to provide the United States with the capability to reach any target in the world within one hour (Prompt Global Strike) using an unmanned hyperson...

У этого термина существуют и другие значения, см. Готы (значения). Готы Готический стиль в одежде Возникновение конец 1970-х Великобритания Годы расцвета 1980-е Направленность музыкальная Распространение ЕвропаАмерикаАзия Австралия Элементы Готическая музыкаГотическая мо...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Частина серії проФілософіяLeft to right: Plato, Kant, Nietzsche, Buddha, Confucius, AverroesПлатонКантНіцшеБуддаКонфуційАверроес Філософи Епістемологи Естетики Етики Логіки Метафізики Соціально-політичні філософи Традиції Аналітична Арістотелівська Африканська Близькосхідна іранська Буддій�...
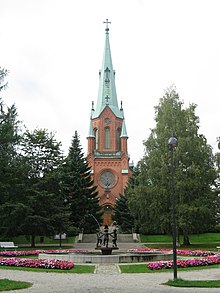
Church in Tampere, Finland Tampere Alexander ChurchTampereen Aleksanterin kirkkoTammerfors AlexanderskyrkanThe Alexander ChurchReligionAffiliationEvangelical Lutheran Church of FinlandEcclesiastical or organizational statusChurch (building)LocationLocationKaakinmaa, Tampere, FinlandGeographic coordinates61°29′50″N 023°44′57″E / 61.49722°N 23.74917°E / 61.49722; 23.74917ArchitectureArchitect(s)Theodor DeckerStyleGothic Revival architectureCompleted1881Specif...

American athlete (born 1978) James CarterCarter before racePersonal informationNationalityAmericanBorn (1978-05-07) May 7, 1978 (age 46)Baltimore, Maryland, United StatesHeight1.83 m (6 ft 0 in)Weight90 kg (198 lb)SportSportAthleticsEvent400 meter hurdlesCollege teamHampton PiratesClubNike Medal record World Championships 2005 Helsinki 400 m hurdles IAAF World Cup 2002 Madrid 400 m hurdles NACAC Championships 2002 San Antonio 4 x 400 m relay 2002 San Antonio 400 ...

American video streaming service go90IndustryOnline videoFoundedOctober 1, 2015 (2015-10-01)DefunctJuly 31, 2018 (2018-07-31)HeadquartersUnited StatesKey peopleBrian Angiolet (SVP Chief Content Officer), Richard Tom (GM and CTO, Verizon Digital Entertainment)ProductsStreaming serviceTelevisionMoviesOwnerVerizon Communications go90 was an American Internet television service and mobile app owned and operated by Verizon Communications. The service was positioned as...

BukharaShahrisabzItchan KalaSamarkandTian Shanclass=notpageimage| Locations of World Heritage Sites in Uzbekistan This is a list of World Heritage Sites in Uzbekistan with properties of cultural and natural heritage in Uzbekistan as inscribed in UNESCO's World Heritage List or as on the country's tentative list. As of 2016, five sites in Uzbekistan are included.[1] In addition to its inscribed sites, Uzbekistan also lists thirty properties on its tentative list.[1] World Heri...

District in Kandal, CambodiaKhsach Kandal ស្រុកខ្សាច់កណ្តាលDistrict (srok)Khsach KandalLocation in CambodiaCoordinates: 11°44′54″N 105°0′41″E / 11.74833°N 105.01139°E / 11.74833; 105.01139Country CambodiaProvinceKandalCommunes18Villages93Population (1998)[1] • Total105,345Time zone+7Geocode0803 This article contains Khmer text. Without proper rendering support, you may see question marks, boxes...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. Prothoma KadambiniGenreDrama BiopikPengembangRajeeb Gangopadhyay Deepanwita GangopadhyaySkenarioSharbari GhoshalBarun ChattopadhyaySutradaraSwornendu SamaddarShamik BoseAnupam HariPresenterSVF EntertainmentPemeranSolanki RoyHoney BafnaNegara asalIndia...

Deutsche Botschaft Maskat Logo Staatliche Ebene Bund Stellung Botschaft Geschäftsbereich Auswärtiges Amt[1] Gründung 1975 Hauptsitz Oman Maskat Botschafter Dirk Lölke Netzauftritt www.maskat.diplo.de Die Deutsche Botschaft Maskat ist die diplomatische Vertretung der Bundesrepublik Deutschland im Sultanat Oman. Inhaltsverzeichnis 1 Lage und Gebäude 2 Auftrag und Organisation 3 Geschichte 4 Siehe auch 5 Weblinks 6 Fußnoten und Einzelnachweise Lage und Gebäude Deutsche Botschaft ...











![{\displaystyle t={\frac {1+{\sqrt[{3}]{19-3{\sqrt {33}}}}+{\sqrt[{3}]{19+3{\sqrt {33}}}}}{3}}\approx 1,839\,286\,755\,21.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffc3b710235dbf4eca4f6a492bd66f787897dce7)






![{\displaystyle {\begin{aligned}\alpha &={\sqrt {{\frac {4}{3}}-{\frac {16}{3\beta }}+{\frac {2\beta }{3}}}}\approx 1,609\,72\\\beta &={\sqrt[{3}]{26+6{\sqrt {33}}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/debe6a11001da1486aed45c37bbc75960a82fc23)