Qui-quadrado
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:
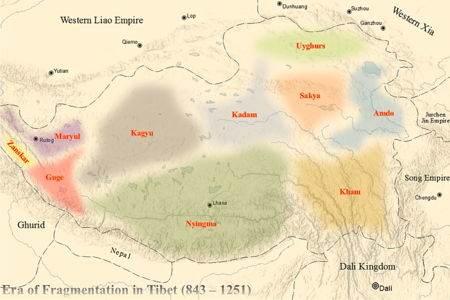
Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Februari 2023. Maryul di Kekaisaran Tibet yang difragmentasi c. 900 Istana Shey, ibu kota Maryul Maryul Ngari (Mar-yul mNgah-ris), berarti dataran rendah Ngari atau dataran rendah Tibet Barat,[1] dahulu adalah suatu kerajaan Tibet Barat di daerah yang ...

Hamza Mendyl Schalke mengadakan sesi latihan sebelum pertandingan dengan Lokomotiv, 2018Informasi pribadiNama lengkap Hamza MendylTanggal lahir 21 Oktober 1997 (umur 26)Tempat lahir Casablanca, MarokoTinggi 179 cm (5 ft 10 in)Posisi bermain BekInformasi klubKlub saat ini LilleNomor 27Karier senior*Tahun Tim Tampil (Gol)2017 – Lille 13 (0)Tim nasional2016 – Maroko 13 (0) * Penampilan dan gol di klub senior hanya dihitung dari liga domestik Hamza Mendyl (lahir 21 Oktobe...

For the 2021 French film, see Between Two Worlds (2021 film). You can help expand this article with text translated from the corresponding article in French. (April 2015) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply...

American professional wrestler The Wrecking Crew (Terminator)Laurinaitis, circa 1988Birth nameMarcus LaurinaitisBorn (1965-02-21) February 21, 1965 (age 59)Philadelphia, PennsylvaniaFamilyJohn Laurinaitis (brother)Road Warrior Animal (brother) James Laurinaitis (nephew)Professional wrestling careerRing name(s)FuryThe TerminatorThe Wrecking CrewBilled height6 ft 1 in (1.85 m)Billed weight270 lb (120 kg; 19 st)Trained byRoad Warrior AnimalJohn LaurinaitisNelso...

Puteri Indonesia 2007Tanggal3 Agustus 2007TempatJakarta Convention Center, Jakarta, IndonesiaPembawa acaraFerdi HasanNadia MulyaPengisi acaraGita GutawaUnguChristopher AbimanyuPenyiaranSCTVPeserta36[1]Tidak tampilNanggroe Aceh DarussalamKalimantan TengahPemenangPutri Raemawasti Jawa Timur← 20062008 →lbs Puteri Indonesia 2007 adalah kontes Puteri Indonesia yang ke-12. Malam grand final pemilihan Puteri Indonesia 2007 diselenggarakan di Jakarta ...

Habit and impulse disorder Compulsive redirects here. For other uses, see Compulsion. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Compulsive behavior – news · newspapers · books · scholar · JSTOR (May 2022) (Learn how and when to remove this template message)Dermatophagia – extreme nail biting / biting...

Opioid antagonist NalmefeneClinical dataTrade namesSelincro, Revex, othersOther namesNalmetrene; 6-Desoxy-6-methylenenaltrexone; CPH-101; JF-1; Lu AA36143; NIH-10365; ORF-11676AHFS/Drugs.comMonographMedlinePlusa605043License data EU EMA: by INN US DailyMed: Nalmefene US FDA: Nalmefene Routes ofadministrationBy mouth, intranasal, intramuscular injection, intravenous injection, subcutaneousDrug classOpioid antagonistATC codeN07BB05 (WHO) Legal statusLegal...

Ne doit pas être confondu avec Lutte ouvrière. Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Cet article ne s'appuie pas, ou pas assez, sur des sources secondaires ou tertiaires (janvier 2021). Pour améliorer la vérifiabilité de l'article ainsi que son intérêt encyclopédique, il est nécessaire, quand des sources primaires sont citées, de les associer à des analyses faites par des sources secondaires. Force ouvrière Cadre Forme juridique Conféd�...
Pembagian administratifJepang Tingkat Prefektur Prefektur Tingkat subprefektur Subprefektur Distrik Tingkat Kotamadya Kota terpilih Kota inti Kota khusus (dihapus) Kota Distrik kota (Tokyo) Kota kecil Desa Tingkat Sub-kotamadya Distrik kota lbs Jepang terbagi menjadi 47 daerah prefektur dan dibagi lagi menjadi daerah sub-prefektur atau langsung menjadi daerah kotamadya yang kemudian dipecah lagi menjadi distrik kota. Susunan struktur Prefektur Sub-prefektur Kotamadya Sub-kotamadya Prefekturpr...

Ne doit pas être confondu avec Locomotive sans foyer. Locomotive 41 018 du Deutsche Reichsbahn Locomotive 242 A 1 de la SNCF. Locomotives, par E. A. Schefer Une locomotive à vapeur est un type de locomotive, c'est un engin moteur pour les chemins de fer, mis en mouvement par une machine à vapeur. Ce type de moteur thermique est le plus couramment utilisé, de la naissance du chemin de fer jusque dans les années 1950. Il reste toujours employé très localement dans certains pays au ...

Tennis Club JuventusTennis Segni distintivi Colori sociali Bianco e nero Simboli zebra Dati societari Città Torino Paese Italia Confederazione ITF Federazione FIT Fondazione 1923 Scioglimento 1949 Presidente Edoardo Agnelli(1923-1935)Enrico Craveri e Giovanni Mazzonis(1935-1936)Emilio de la Forest de Divonne(1936-1941)Piero Dusio(1941-1949) Allenatore informazione sconosciuta Impianto sportivo Campo Juventus(1923-1939)[1]Stadio Tennistico Juventus[2](1942-1949) (5 ...

Questa voce sull'argomento squadre di hockey su ghiaccio è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. MHC MartinHockey su ghiaccio Segni distintivi Uniformi di gara Casa Trasferta Colori sociali bianco-blu Dati societari Città Martin Paese Slovacchia Confederazione IIHF Federazione SZL'H Campionato Extraliga Fondazione 1932 Presidente Jaroslav Zigo Allenatore Ladislav Spišiak e Marian Brúsil Impianto di gioco Zimný Štadión Martin(4.200 ...

American physicist (1926–2023) This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Lewis M. Branscomb – news · newspapers · books · scholar · JSTOR (July 202...

1st DivisionOfficial division logoActive1941–20032005–presentCountry Kingdom of Iraq (1941–58) Republic of Iraq (1958–68) Ba'athist Iraq (1968–2003) Iraq (2005–present)BranchIraqi ArmyTypeMotorised InfantrySizeDivisionPart ofAnbar Operations CommandGarrison/HQCamp FallujahEngagements Anglo-Iraqi War Iran–Iraq War Operation Fath ol-Mobin Second Battle of Al Faw Gulf War Battle of Khafji Iraq War Second Battle of Fallujah Battle of Basra (2008) War in Iraq (2013-17) Nort...

2018 single by Brothers OsborneShoot Me StraightSingle by Brothers Osbornefrom the album Port Saint Joe ReleasedJanuary 16, 2018 (2018-01-16)[1]GenreCountry rock, southern rockLength6:24 (album version)3:27 (radio edit)LabelEMI NashvilleSongwriter(s)John OsborneT.J. OsborneLee Thomas MillerProducer(s)Jay JoyceBrothers Osborne singles chronology It Ain't My Fault (2017) Shoot Me Straight (2018) Burning Man (2018) Shoot Me Straight is a song recorded by American country m...

Red 2Logo ufficiale del filmLingua originaleinglese Paese di produzioneStati Uniti d'America Anno2013 Durata116 min Rapporto2,35:1 Genereazione, commedia RegiaDean Parisot Soggettopersonaggi creati da Warren Ellis e Cully Hamner SceneggiaturaErich Hoeber, Jon Hoeber ProduttoreLorenzo di Bonaventura, Mark Vahradian, Raphaël Benoliel, Alexander Dostal, Cliff Lanning Produttore esecutivoJake Myers, David Ready, John Brooks Klingenbeck Casa di produzioneDC Entertainment, Di Bonaventura Pictu...

ميركوسور الكتلة التجارية هي نوع من اتفاق بين الحكومات، في كثير من الأحيان جزء من منظمة حكومية دولية إقليمية، حيث الحواجز أمام التجارة الإقليمية (التعريفات الجمركية والحواجز غير الجمركية) يتم تخفيضها أو الغائها بين الدول المشاركة.[1][2][3] الوصف واحدة من التكتلات...

Pierre-Simon Laplace Analisis matematika → Analisis kompleksAnalisis kompleks Bilangan kompleks Bilangan real Bilangan imajiner Bidang kompleks Konjugat kompleks Bilangan kompleks satuan Fungsi kompleks Fungsi bernilai kompleks Fungsi analitik Fungsi holomorfik Persamaan Cauchy–Riemann Deret pangkat formal Teori dasar Nol dan kutub Teorema integral Cauchy Primitif lokal Rumus integral Cauchy Bilangan lilitan Deret Laurent Kesingularan terpencil Teorema residu Peta konformal Lema Schwarz F...
Bài này viết về giải thưởng của nữ. Đối với giải thưởng của nam, xem Cầu thủ xuất sắc nhất thế kỷ của FIFA. Cầu thủ nữ xuất sắc nhất thế kỷ của FIFA (tiếng Anh: FIFA Female Player of the Century) là giải thưởng do FIFA tổ chức nhằm tìm ra cầu thủ bóng đá nữ xuất sắc nhất thế kỷ 20. Michelle Akers của Hoa Kỳ và Tôn Văn là những người chiến thắng trong buổi trao thưởng tại Roma...

Stringed instrument playing technique G run in G major variation[1] Playⓘ contains both hammer-ons and a pull-off. A hammer-on is a playing technique performed on a stringed instrument (especially on a fretted string instrument, such as a guitar) by sharply bringing a fretting-hand finger down on to the fingerboard behind a fret, causing a note to sound. This technique is the opposite of the pull-off. Passages in which a large proportion of the notes are performed as hammer-ons and ...












































