Poligonal topográfica
|
Read other articles:

Waterfall in Balochistan, PakistanPir Ghaib Waterfallsپیر غیب کا آبشارPir Ghaib Waterfalls in BolanLocationBolan, Balochistan, PakistanCoordinates29°46′N 67°17′E / 29.76°N 67.29°E / 29.76; 67.29TypeCascadeTotal height50 ft (15 m)Number of drops2 Pir Ghaib Waterfalls are waterfalls situated in the Bolan Valley, 70 kilometres (43 mi) from Quetta, in Balochistan, Pakistan.[1] Here a waterfall cascades down rocky mountain side ma...

Artikel ini tidak memiliki referensi atau sumber tepercaya sehingga isinya tidak bisa dipastikan. Tolong bantu perbaiki artikel ini dengan menambahkan referensi yang layak. Tulisan tanpa sumber dapat dipertanyakan dan dihapus sewaktu-waktu.Cari sumber: Hanif Andarevi – berita · surat kabar · buku · cendekiawan · JSTOR artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu And...
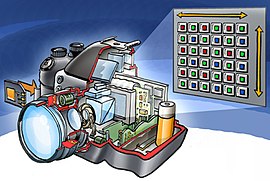
artikel ini perlu dirapikan agar memenuhi standar Wikipedia. Tidak ada alasan yang diberikan. Silakan kembangkan artikel ini semampu Anda. Merapikan artikel dapat dilakukan dengan wikifikasi atau membagi artikel ke paragraf-paragraf. Jika sudah dirapikan, silakan hapus templat ini. (Pelajari cara dan kapan saatnya untuk menghapus pesan templat ini) Sebuah kamera digital SiPix yang didekatkan dengan sebuah kotak korek api untuk membandingkan ukurannya. Kamera digital adalah sebuah perangkat el...

Bronze sculpture by Pete Helzer in Eugene, Oregon, U.S. The StorytellerThe sculpture in 2015ArtistPete HelzerTypeSculptureMediumBronzeSubjectKen KeseyLocationEugene, Oregon, United StatesCoordinates44°02′59″N 123°05′33″W / 44.04980°N 123.09259°W / 44.04980; -123.09259 The Storyteller, also known as the Ken Kesey Memorial,[1] is an outdoor bronze sculpture by Pete Helzer, installed at Kesey Square (located at Broadway and Willamette Street) in Eugene...

Skema Sel Haploid yang Melebur Membentuk Sel Diploid Diploid (serapan dari Belanda: diploïdecode: nl is deprecated ) ialah sebutan untuk sel atau individu yang memiliki sel dengan dua set genom.[1] Setiap genom dalam sel berpasangan dengan homolognya berdasarkan ukuran panjang kromosom.[2] Sel diploid terbentuk dari fertilisasi sel-sel gamet yang haploid.[1] Sel-sel gamet haploid melebur sehingga kromosom-kromosom bercampur dalam satu sel membentuk sel diploid.[3&...

The Revenue Act of 1928 (May 29, 1928, ch. 852, 45 Stat. 791), formerly codified in part at 26 U.S.C. sec. 22(a), is a statute introduced as H.R. 1[1] and enacted by the 70th United States Congress in 1928 regarding tax policy. Section 605 of the Act provides that In case a regulation or Treasury decision relating to the internal revenue laws is amended by a subsequent regulation or Treasury decision, made by the Secretary or by the Commissioner with the approval of the Secretary, suc...

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. La mise en forme de cet article est à améliorer (juin 2021). La mise en forme du texte ne suit pas les recommandations de Wikipédia : il faut le « wikifier ». Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus. Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliogr...

History United States NameJohn Gilpin OwnerPierce & Hunnewell, Boston BuilderSamuel Hall, East Boston LaunchedSeptember 1852 Fate Collided with iceberg 29 January 1858 Abandoned 30 January 1858 NotesDesigned by Samuel Hall General characteristics Class and typeExtreme clipper Length195 ft. ; 205 ft. LOA Beam37 ft. Draft22 ft. Notes2 decks[1][2] John Gilpin was an 1852 clipper in the California trade, named after the literary character John Gilpin. The ship was known ...

Intergovernmental naval operations This section needs to be updated. The reason given is: List of countries presently contributing is out of date. Please help update this article to reflect recent events or newly available information. (December 2021) Ships assigned to Combined Task Force One Five Zero (CTF-150) assemble in a formation in the Gulf of Oman, 6 May 2004 Combined Task Force 150 (CTF-150) is a multinational coalition naval task force working under the 34-nation coalition of Combin...

穆罕默德·达乌德汗سردار محمد داود خان 阿富汗共和國第1任總統任期1973年7月17日—1978年4月28日前任穆罕默德·查希爾·沙阿(阿富汗國王)继任穆罕默德·塔拉基(阿富汗民主共和國革命委員會主席團主席) 阿富汗王國首相任期1953年9月7日—1963年3月10日君主穆罕默德·查希爾·沙阿 个人资料出生(1909-07-18)1909年7月18日 阿富汗王國喀布尔逝世1978年4月28日(...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...
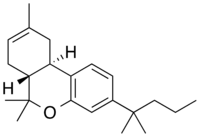
Chemical compound JWH-133Identifiers IUPAC name (6aR,10aR)-3-(1,1-Dimethylbutyl)-6a,7,10,10a-tetrahydro -6,6,9-trimethyl-6H-dibenzo[b,d]pyran CAS Number259869-55-1 NPubChem CID6918505IUPHAR/BPS747ChemSpider5293702 YUNIITDG8048RDAChEBICHEBI:146243ChEMBLChEMBL371214 YCompTox Dashboard (EPA)DTXSID30426077 Chemical and physical dataFormulaC22H32OMolar mass312.497 g·mol−13D model (JSmol)Interactive image SMILES O3c1cc(ccc1[C@@H]2C\C(=C/C[C@H]2C3(C)C)C)C(C)(C)CCC InChI InChI=...

American politician This article is about the U.S. Representative. For other people with the same or similar names, see Charles Cooper. Charles Merian CooperMember of the U.S. House of Representativesfrom Florida's 2nd districtIn officeMarch 4, 1893 – March 3, 1897Preceded byRobert BullockSucceeded byRobert Wyche Davis15th Florida Attorney GeneralIn officeJanuary 13, 1885 – January 8, 1889GovernorEdward A. PerryPreceded byGeorge P. RaneySucceeded byWilliam Ba...

Religion with formalized beliefs and rituals Priests lay their hands on the ordinands during a Roman Catholic rite of ordination. The Catholic Church, the largest Christian denomination, is an example of an organized religion. Organized religion, also known as institutional religion, is religion in which belief systems and rituals are systematically arranged and formally established, typically by an official doctrine (or dogma), a hierarchical or bureaucratic leadership structure, and a codif...

German infantry division This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 19th Waffen Grenadier Division of the SS 2nd Latvian – news · newspapers · books · scholar · JSTOR (February 2016) (Learn how and when to remove this message) 19th Waffen Grenadier Division of the SS (2nd Latvian)Unit insigniaActiv...

العلاقات الإسرائيلية الشمال مقدونية إسرائيل شمال مقدونيا إسرائيل شمال مقدونيا تعديل مصدري - تعديل العلاقات الإسرائيلية الشمال مقدونية هي العلاقات الثنائية التي تجمع بين إسرائيل وشمال مقدونيا.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة ...

German noble and general (1655–1707) Louis WilliamMargrave of Baden-BadenPortrait in 1705Born(1655-04-08)8 April 1655Hôtel de Soissons, Paris, FranceDied4 January 1707(1707-01-04) (aged 51)Schloss Rastatt, Rastatt, Baden, Holy Roman EmpireBurialStiftskirche, Baden-BadenSpouseSibylle of Saxe-LauenburgIssueDetailLouis George, Margrave of Baden-BadenAuguste, Duchess of OrléansAugustus George, Margrave of Baden-BadenHouseHouse of ZähringenFatherFerdinand Maximilian of Baden-BadenMotherL...

Themysciraluogo fittizioThemyscira così come appare in Wonder Woman Altri nomiIsola Paradiso CreazioneUniversoUniverso DC IdeatoreWilliam Moulton MarstonHarry G. Peter 1ª app. inCome Isola Paradiso:All Star Comics n. 8 (dicembre 1941)Come Themyscira:Wonder Woman (vol. 2[1]) n. 1 (febbraio 1987) Caratteristiche immaginarieTipoIsola/Città-Stato PianetaTerra Abitanti Wonder Woman Regina Ippolita Antiope Donna Troy Artemide Wonder Woman di Terra-Due Amazzoni Manuale Themyscira (/ˌθɛ...

Pour les articles homonymes, voir Lozère. Lozère Administration Pays France Région Occitanie Création du département 4 mars 1790 (234 ans) Chef-lieu(Préfecture) Mende Sous-préfectures Florac Trois Rivières Président duconseil départemental Laurent Suau (DVC) Préfet Philippe Castanet[1] Code Insee 48 Code ISO 3166-2 FR-48 Code Eurostat NUTS-3 FR814 Démographie Gentilé Lozérien Population 76 519 hab. (2021) Densité 15 hab./km2 Géographie Coordonn...

Israeli politician (born 1973) Avihai BoaronBoaron in 2021Faction represented in the Knesset2023Likud2024–Likud Personal detailsBorn (1973-07-12) 12 July 1973 (age 51)[1]Netanya, Israel Avihai Avraham Boaron (Hebrew: אביחי בוארון) (born 12 July 1973) is an Israeli settler activist and politician[citation needed] currently serving as a member of the Knesset for Likud since July 2024.[2] He previously held the position from April to October 2023. He fir...




















