Notação de Voigt
|
Read other articles:

Emanuel Melkiades Laka Lena Anggota Dewan Perwakilan Rakyat Republik IndonesiaPetahanaMulai menjabat 1 Oktober 2019PresidenJoko WidodoDaerah pemilihanNusa Tenggara Timur II Informasi pribadiLahir10 Desember 1976 (umur 47)Kupang, Nusa Tenggara TimurPartai politikGolkarSuami/istriMindriyati AstiningsihAnak1Alma materUniversitas Sanata DharmaSunting kotak info • L • B Emanuel Melkiades Laka Lena (lahir 10 Desember 1976) adalah politikus Indonesia yang menjabat sebagai angg...

Lempok durian Bengkulu Lempok durian Bangka Lempok durian, sering disebut juga dodol durian atau lempuk durian, serta dalam bahasa Tionghoa disebut dengan (Hanzi: 榴槤粄; Hakka: Liu-lian-pan), adalah salah satu jenis lempok yang dibuat dengan bahan daging durian. Lempok durian populer sebagai jajanan khas dari beberapa daerah di Indonesia, terutama di Sumatra seperti Bengkulu, Jambi, Bengkalis, Pekanbaru, Palembang, Bangka Belitung, Lampung, serta Kalimantan misalnya Pontianak dan Samarind...

Nigerian-British pharmacist and Professor of Pharmacy Ijeoma UchegbuIjeoma Uchegbu at the Oxford Union Science Debate 2018Alma materUniversity of Benin University of Lagos University of LondonKnown forNanoparticle drug deliveryScientific careerInstitutionsUniversity of Strathclyde University College London Websitehttp://www.nanomerics.com Ijeoma Uchegbu is a Nigerian-British Professor of Pharmacy at University College London where she held the position of Pro-Vice Provost for Africa...

Joseph Bonanno Joseph Bonanno, all'anagrafe Giuseppe Bonanno, e soprannominato Joe Bananas[1] (Castellammare del Golfo, 18 gennaio 1905 – Tucson, 11 maggio 2002), è stato un mafioso italiano naturalizzato statunitense, legato a Cosa nostra statunitense e capo della famiglia mafiosa di New York che porta il suo nome. Indice 1 Biografia 1.1 Morte 2 Boss della famiglia Bonanno 3 Opere 4 Note 5 Voci correlate 6 Altri progetti 7 Collegamenti esterni Biografia Giuseppe Bonanno nacque a C...

Vukovar ВуковарKotaKota VukovarGrad Vukovar BenderaLambang kebesaranJulukan: Grad Heroj (Kota Pahlawan)Lokasi Kotamadya VukovarNegara KroasiaRegionPodunavljeKabupaten Vukovar-SyrmiaPemerintahan • Wali KotaIvan Penava (Independen)Luas • Kota100,26 km2 (3,871 sq mi)Ketinggian108 m (354 ft)Populasi (2011)[1] • Kota27.683 • Kepadatan2,8/km2 (7,2/sq mi) • Perkotaan26.468Demo...

أخلاقيات الإعلام هي قسم فرعي من الأخلاقيات التطبيقية التي تتعلق بالمبادئ والمعايير الأخلاقية الخاصة بالإعلام، وتتضمن الإعلام الإذاعي والأفلام والمسرح والفنون والإعلام المطبوع والإنترنت. ويغطي هذا المجال موضوعات مختلفة وجدلية بصورة كبيرة، بداية من صحافة الحروب إلى بين�...

Ansbach Lambang kebesaranLetak Ansbach NegaraJermanNegara bagianBayernWilayahMittelfrankenKreisDistrik perkotaanPemerintahan • Lord MayorCarda Seidel (BAP/FWG/ödp)Luas • Total99,92 km2 (3,858 sq mi)Ketinggian405 m (1,329 ft)Populasi (2013-12-31)[1] • Total39.839 • Kepadatan4,0/km2 (10/sq mi)Zona waktuWET/WMPET (UTC+1/+2)Kode pos91522Kode area telepon0981Pelat kendaraanANSitus webwww.ansbach.de Untuk me...

Season of television series Winx ClubSeason 5No. of episodes26ReleaseOriginal networkNickelodeon, Rai 2Original release16 October 2012 (2012-10-16)[1] –24 April 2013 (2013-04-24)Season chronology← PreviousSeason 4Next →Season 6List of episodes The fifth season of Winx Club premiered on Nickelodeon in the United States on 26 August 2012 and on Rai 2 in Italy on 16 October 2012. It is the first season produced with Nickelodeon.[2] It is the first ...

Nemanja Rnić Nazionalità Jugoslavia Serbia e Montenegro (dal 2003) Serbia (dal 2006) Altezza 180 cm Peso 74 kg Calcio Ruolo Difensore Squadra Wolfsberger Carriera Squadre di club1 2002-2008 Partizan152 (2)2008-2010 Anderlecht13 (0)2010-2011→ Germinal Beerschot10 (0)2011-2012 Partizan25 (0)2013 Hoverla13 (0)2013-2021 Wolfsberger183 (3) Nazionale 2005 Serbia e Montenegro1 (0)2006 Serbia U-2119 (0)2008 Serbia2 (0) Palmarès Europei ...

Aiguebelette-le-Lac Égouabelètacode: frp is deprecated (Arpitan)KomunePemandangan Aiguebelette-le-Lac Lambang kebesaranAiguebelette-le-Lac Lokasi di Region Auvergne-Rhône-Alpes Aiguebelette-le-Lac Koordinat: 45°32′19″N 5°48′56″E / 45.5386°N 5.8156°E / 45.5386; 5.8156Koordinat: 45°32′19″N 5°48′56″E / 45.5386°N 5.8156°E / 45.5386; 5.8156NegaraPrancisRegionAuvergne-Rhône-AlpesDepartemenSavoieArondisemenChamb�...

Extinct genus of fishes MeridensiaTemporal range: Anisian–Ladinian PreꞒ Ꞓ O S D C P T J K Pg N Meridensia meridensis fossil Scientific classification Kingdom: Animalia Phylum: Chordata Class: Actinopterygii Order: †Perleidiformes Genus: †MeridensiaAndersson, 1916 Binomial name †Meridensia meridensis(de Alessantri, 1910) Meridensia is an extinct genus of prehistoric ray-finned fish that lived during the Anisian and Ladinian ages of the Middle Triassic epoch in what is now southern ...

此條目没有列出任何参考或来源。 (2013年2月8日)維基百科所有的內容都應該可供查證。请协助補充可靠来源以改善这篇条目。无法查证的內容可能會因為異議提出而被移除。 莱奥波尔多·加尔铁里Leopoldo Fortunato Galtieri Castelli 阿根廷总统(實質)任期1981年12月22日—1982年6月18日副总统Víctor Martínez前任卡洛斯·拉科斯特继任阿尔弗雷多·奥斯卡·圣琼 个人资料出生(1926-07-15)1926�...

坐标:43°11′38″N 71°34′21″W / 43.1938516°N 71.5723953°W / 43.1938516; -71.5723953 此條目需要补充更多来源。 (2017年5月21日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:新罕布什尔州 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) الحفيره (مركز ظلم) قرية تقسيم إداري قائمة الدول السعودية مناطق السعودية محافظة الطائف، منطقة م�...

Chinese painter and poet (1470–1524) In this Chinese name, the family name is Tang (唐).Tang YinBorn1470Died1524 (aged 54)EducationProtégé of Wen LinKnown forPoetry, Painting Tang Yin (Chinese: 唐寅; pinyin: Táng Yín; Cantonese Yale: Tong Yan; 1470–1524), courtesy name Bohu (伯虎), was a Chinese painter, calligrapher, and poet of the Ming dynasty period. Even though he was born during the Ming dynasty, many of his paintings, especially those of people, were illus...
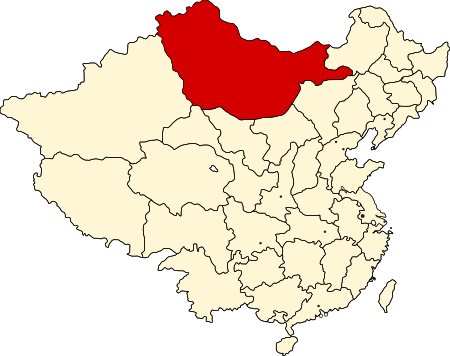
Historical region This article is about a historical region of the Qing dynasty. For the present day country, see Mongolia. For the former communist state often referred to as Outer Mongolia, see Mongolian People's Republic. Outer Mongolia and Inner Mongolia within the Qing dynasty. Location of Mongolia Area as part of the Republic of China (claim only) Map of the Republic of China in 1914 After the Treaty of Kyakhta (North) Mongolia in 1915 This article contains Mongolian script. Without pro...

Reconnaissance unmanned aerial vehicle ScanEagle A ScanEagle flying in 2016 Role Small unmanned surveillance and reconnaissance aerial vehicleType of aircraft National origin United States Manufacturer Insitu First flight 20 June 2002 Introduction 2005 (U.S. Navy) Primary users United States NavyUnited States Marine Corps Royal Australian Navy See Operators section for others Produced 2002–present Developed from Insitu SeaScan Developed into Boeing Insitu RQ-21 Blackjack The Boeing Ins...

This article is an orphan, as no other articles link to it. Please introduce links to this page from related articles; try the Find link tool for suggestions. (August 2016) Paper Reclaim Ltd v Aotearoa International LtdCourtCourt of Appeal of New ZealandFull case namePaper Reclaim Ltd v Aotearoa International Ltd Decided14 March 2006Citations[2006] NZCA 27 (14 March 2006); [2006] 3 NZLR 188; (2006) 8 NZBLC 101,685; (2006) 11 TCLR 544TranscriptjudgmentCourt membershipJudges sittingAnderson P,...

Questa voce o sezione sull'argomento lingue è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti più precisamente. Segui i suggerimenti del progetto di riferimento. CimbroZimbar, zimbar zungParlato in Italia...

ロシアのウクライナ侵攻における戦争犯罪 (英語:War crimes in the Russian invasion of Ukraine、フランス語:Crimes de guerre lors de l'invasion russe de l'Ukraine、スペイン語:Crímenes de guerra en la invasión rusa de Ucrania、ロシア語:Военные преступления в период вторжения России на Украину、中国語:俄罗斯入侵乌克兰的战争罪行、アラビア語:جرائم الحرب خلال الغزو الر�...
![{\displaystyle {\boldsymbol {X}}=\left[{\begin{matrix}x_{11}&x_{12}\\x_{21}&x_{22}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7032923ab43695db652ca35f8d83a8cce7c283ea)

![{\displaystyle {\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{xx}&\sigma _{xy}&\sigma _{xz}\\\sigma _{yx}&\sigma _{yy}&\sigma _{yz}\\\sigma _{zx}&\sigma _{zy}&\sigma _{zz}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3682cc336516f2025f50067199b9414439f9b384)

![{\displaystyle {\boldsymbol {\epsilon }}=\left[{\begin{matrix}\epsilon _{xx}&\epsilon _{xy}&\epsilon _{xz}\\\epsilon _{yx}&\epsilon _{yy}&\epsilon _{yz}\\\epsilon _{zx}&\epsilon _{zy}&\epsilon _{zz}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0921328114e178f074d4509a81a9c9001f2bf58e)






![{\displaystyle {\boldsymbol {\sigma }}=\left[{\begin{matrix}\sigma _{11}&\sigma _{12}&\sigma _{13}\\\sigma _{21}&\sigma _{22}&\sigma _{23}\\\sigma _{31}&\sigma _{32}&\sigma _{33}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6013e0552a56a7a266e368145fb181089da6838)




