Geometria euclidiana
|
Read other articles:
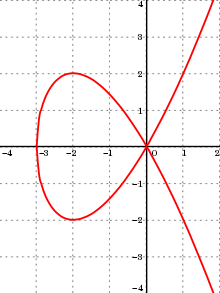
Curve defined as zeros of polynomials The Tschirnhausen cubic is an algebraic curve of degree three.This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (August 2023) (Learn how and when to remove this template message) In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero se...

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada Desember 2022. Lexy KolkerKolker, 2018LahirAlexa Rose Kolker17 Agustus 2009 (umur 14)Los Angeles, CaliforniaPekerjaanAktrisTahun aktif2015–sekarang Alexa Rose Lexy Kolker (lahir 17 Agustus 2009),[1] lebih dikenal sebagai Lexy Kolker, adalah seora...

Experimental solid-fuel research rocket X-17 redirects here. For other uses, see X17 (disambiguation). Lockheed X-17 TypeAtmospheric reentry testingProduction historyManufacturerLockheed CorporationSpecificationsLength40 ft 4 in (12.29 m)Diameter1st stage: 2 ft 7 in (0.79 m)2nd stage: 1 ft 5 in (0.43 m)3rd stage: 0 ft 9.7 in (0.246 m)Wingspan7 ft 7 in (2.31 m)Engine1st stage:1× Thiokol XM20 Sergeant solid-fuel rocket,...

1898 Wyoming gubernatorial election ← 1894 November 8, 1898 1902 → Turnout32.62% of Total Population 0.84 Nominee DeForest Richards Horace C. Alger Party Republican Democratic Popular vote 10,383 8,989 Percentage 52.43% 45.39% Governor before election William A. Richards Republican Elected Governor DeForest Richards Republican Elections in Wyoming Federal government Presidential elections 1892 1896 1900 1904 1908 1912 1916 1920 1924 1928 1932 1936 1940 1944 ...

American computer scientist Xuedong Huangin 2017Born (1962-10-20) October 20, 1962 (age 61)ChinaCitizenshipUnited StatesAlma materUniversity of Edinburgh, Tsinghua University, Hunan UniversityAwardsNational Academy of Engineering Member, American Academy of Arts and Sciences Member, IEEE Bose Industrial Leader Award, Asian American Corporate Leadership Award, ACM Fellow, IEEE FellowScientific careerFieldsSpeech Recognition, Machine translation, Natural Language Processing, AI, Compu...

Nama ini menggunakan kebiasaan penamaan Filipina; nama tengah atau nama keluarga pihak ibunya adalah López dan marga atau nama keluarga pihak ayahnya adalah Locsin. Locsin dalam acara Asia Society di New York City pada September 2017. Teodoro Teddy Boy López Locsin Jr. PLH (lahir 15 November 1948), adalah seorang politikus, diplomat, pengacara dan mantan wartawan asal Filipina. Ia menjadi anggota kongres untuk Dapil 1 Makati dari 2001 sampai 2010 dan kemudian menjabat sebagai Dubes Fil...

1984 Indian filmPartyDirected byGovind NihalaniWritten byGovind NihalaniBased onPartyby Mahesh ElkunchwarProduced byNFDCStarringManohar SinghVijaya MehtaRohini HattangadiOm PuriNaseeruddin ShahCinematographyGovind NihalaniEdited byRenu SalujaRelease date 1984 (1984) Running time118 minutesCountryIndiaLanguageHindi Party is a 1984 Hindi-language film directed by Govind Nihalani. The film boasted an ensemble cast, including Vijaya Mehta, Manohar Singh, Om Puri, Naseeruddin Shah, and Rohin...
Medical conditionComplications of pregnancy810 women die every day from preventable causes related to pregnancy and childbirth. 94% occur in low and lower middle-income countries.SpecialtyObstetricsComplicationsNumerous biological and environmental complicationsRisk factorsNumerous biological and environmental conditions Complications of pregnancy are health problems that are related to, or arise during pregnancy. Complications that occur primarily during childbirth are termed obstetric labor...

2023 film by Wim Wenders This article is about the 2023 film. For other uses, see Perfect Days (disambiguation). Perfect DaysJapanese theatrical release posterDirected byWim WendersWritten by Wim Wenders Takuma Takasaki Produced by Wim Wenders[1] Takuma Takasaki[1] Koji Yanai[1] Starring Kōji Yakusho Tokio Emoto Arisa Nakano Aoi Yamada Yumi Asō Sayuri Ishikawa Tomokazu Miura Min Tanaka CinematographyFranz Lustig[1]Edited byToni Froschhammer[1]Producti...

This article is part of a series onPolitics of Greece Constitution Constitutional history Human rights Executive Head of state President of the Republic (list): Katerina Sakellaropoulou Presidential Departments Government Prime Minister (list): Kyriakos Mitsotakis Cabinet: Kyr. Mitsotakis II Legislature Speaker: Konstantinos Tasoulas Presidium Conference of Presidents Parliamentary committees Constituencies Apportionment Judiciary Supreme courts Special Highest Court Court of Cassation Counc...

Fārūq I d'EgittoRe Fārūq I d'Egitto nel 1946Re d'Egitto e del SudanStemma In carica28 aprile 1936 –26 luglio 1952 PredecessoreFuʾād I SuccessoreFuʾād II Nome completoFārūq ibn Fu'ād TrattamentoSua Maestà Altri titoliSovrano di Nubia, Kordofan e Darfur NascitaPalazzo 'Abidin, Il Cairo, 11 febbraio 1920 MorteOspedale San Camillo, Roma, 18 marzo 1965 (45 anni) Luogo di sepolturaMoschea di al-Rifa'i Casa realeDinastia di Muhammad Alì PadreFu'ad I d'Egitto MadreNazli Sabr...

Iranian footballer (born 1962) Farshad Pious Pious in Azadi StadiumPersonal informationDate of birth (1962-01-12) 12 January 1962 (age 62)Place of birth Tehran, IranPosition(s) ForwardTeam informationCurrent team DamashSenior career*Years Team Apps (Gls)1980–1983 Rah Ahan 28 (21)1983–1984 Shahin 6 (5)1984–1985 Nirooye Havaei 24 (20)1985–1988 Persepolis 69 (60)1988–1989 Al-Ahli 12 (9)1989–1997 Persepolis 192 (169)Total 327 (288)International career1984–1994 Iran[1] 3...

هذه المقالة يتيمة إذ تصل إليها مقالات أخرى قليلة جدًا. فضلًا، ساعد بإضافة وصلة إليها في مقالات متعلقة بها. (سبتمبر 2016) فضائل المدينة المنورة حرم النبي محمد صلى الله عليه وسلم المدينة المنورة على غير المسلمين، ودعى لأهل المدينة بالبركة، وحفظ الله المدينة من الطاعون والمسيح �...

Cet article est une ébauche concernant le Nouveau-Brunswick. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Les Premières nations du Nouveau-Brunswick sont l'ensemble des Premières nations (au sens de « bande indienne ») présentes sur le territoire du Nouveau-Brunswick au Canada. Celles-ci totalisent plus de 10 000 personnes, surtout des Micmacs et des Malécites. Carte des réserves indien...

لمعانٍ أخرى، طالع الجمعة (توضيح). هذه المقالة عن يوم الجمعة. لسورة الجمعة، طالع سورة الجمعة. الجمعةمعلومات عامةصنف فرعي من يوم الأسبوعيومعيد جزء من أسبوع سُمِّي باسم القائمة ... فريغفينوس56المعدن (وو شينغ) الرمز C الترتيب في التسلسل 56 الخميس السبت تعديل - تعديل...

Jo MielzinerScénographie de The Doctor's Dilemma (1927)BiographieNaissance 19 mars 190114e arrondissement de ParisDécès 15 mars 1976 (à 74 ans)New YorkNom de naissance Joseph MielzinerNationalité américaineFormation Ethical Culture Fieldston School (en)Pennsylvania Academy of the Fine ArtsActivités Directeur artistique, chef décorateur, décorateur de théâtre, scénographe, metteur en scèneConjoint Marya Mannes (en)Autres informationsDistinctions Liste détailléeTony Award de...

Dieser Artikel beschreibt die Bundesstraße 111 in Deutschland. Zur gleichnamigen Straße in Österreich siehe Gailtal Straße. Vorlage:Infobox hochrangige Straße/Wartung/DE-B Bundesstraße 111 in Deutschland Karte Verlauf der B 111 Alle Koordinaten: OSM | WikiMap Basisdaten Betreiber: Deutschland Bundesrepublik Deutschland Straßenbeginn: Gützkow(53° 56′ 55″ N, 13° 22′ 4″ O53.94851413.367822) Straßenende: Mellenthin(53° 54�...

University in Bucharest, Romania Politehnica University of BucharestUniversitatea Națională de Știință și Tehnologie POLITEHNICA BucureștiSeal of the Politehnica University of BucharestFormer namesPolitehnica School of Bucharest (1920–1948)Polytechnic Institute of Bucharest (1948–1992)TypePublicEstablished10 June 1920; 104 years ago (1920-06-10)1864 - School of Bridges and Roads, Mines and Architecture1818 - School for Surveying EngineersRectorMihnea CostoiuAcadem...

СтаницаДагестанская 44°22′27″ с. ш. 40°00′45″ в. д.HGЯO Страна Россия Субъект Федерации Адыгея Муниципальный район Майкопский Сельское поселение Краснооктябрьское История и география Основан 1863 Прежние названия Дагестанский Высота центра 304 м Часовой пояс UT...

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (December 2020) (Learn how and when to remove this message) Meriones History United Kingdom NameMeriones NamesakeMeriones OwnerChina Mutual Steam Nav Co Ltd OperatorAlfred Holt & Co Port of registryLiverpool BuilderPalmers Sb and Iron Co, Hebburn Yard number921 Launched19 August 1921 CompletedSeptember 1922 I...