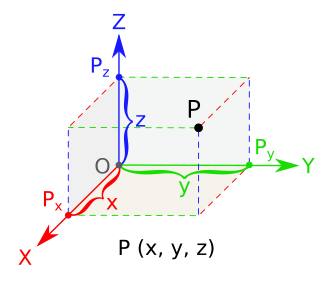
Dimensão
|
Read other articles:

Cipoh ekor putih Status konservasi Risiko Rendah (IUCN 3.1)[1] Klasifikasi ilmiah Domain: Eukaryota Kerajaan: Animalia Filum: Chordata Kelas: Aves Ordo: Passeriformes Superfamili: Malaconotoidea Famili: Aegithinidae Genus: Aegithina Spesies: Aegithina nigroluteaMarshall, GFL, 1876 Peta persebaran Cipoh Marshall [2] ( Aegithina nigrolutea ), juga dikenal sebagai cipoh ekor putih, adalah burung penyanyi dalam genus Aeg...

Halaman ini berisi artikel tentang struktur tertentu yang dikenal sebagai aljabar non-asosiatif. Untuk non-asosiasi secara umum, lihat Non-asosiasi. Struktur aljabar → Teori gelanggangTeori gelanggang Konsep dasarGelanggang • Subgelanggang • Ideal • Gelanggang hasil bagi • Ideal pecahan • Gelanggang hasil bagi total • Gelanggang produk • Produk bebas dari aljabar asosiatif • Produk tensor gelanggang Gelanggang homomorfisme • Kernel • Keautomorfan dalam • Endomorfisme F...

Choice of colors used in design Colour scheme and Color schemes redirect here. For the 1943 detective novel by Ngaio Marsh, see Colour Scheme. For the 1985 album by vibraphonist Bobby Hutcherson, see Color Schemes. Color palette redirects here. For the painter's tool, see Palette (painting). In color theory, a color scheme is a combination of 2 or more colors used in aesthetic or practical design. Aesthetic color schemes are used to create style and appeal. Colors that create a harmonious fee...

No. 644 Squadron RAFActive23 Feb 1944 – 1 Sep 1946Country United KingdomBranch Royal Air ForceTypeInactiveRoleAirborne Assault SOE Supply TransportPart ofNo. 38 Group RAF[1]Motto(s)Latin: Dentes draconis serimus(Translation: We sow the dragon's teeth)[2]InsigniaSquadron Badge heraldryIn front of an increscent, a Pegasus rampant[3] The Pegasus signifies the Squadron's association with the Parachute Brigade[4]Squadron Codes2P (Feb 1944 – Sep 1946)[5...

American film director, producer, screenwriter and cinematographer (1904–1975) For other people named George Stevens, see George Stevens (disambiguation). George StevensStevens with his Oscar for directing Giant, 1957BornGeorge Cooper Stevens(1904-12-18)December 18, 1904Oakland, California, U.S.DiedMarch 8, 1975(1975-03-08) (aged 70)Lancaster, California, U.S.Resting placeForest Lawn Memorial Park, Hollywood HillsOccupationsDirectorcinematographeractorwriterproducerYears active191...

Albanian politician and general Major GeneralPetrit DumeBorn(1920-05-20)20 May 1920Starje, Principality of AlbaniaDied5 December 1975(1975-12-05) (aged 55)Service/branchLANÇAlbanian People's ArmyYears of service1942-75RankMajor GeneralBattles/warsWorld War IISignature Petrit Dume (20 May 1920 – 5 December 1975) was an Albanian general and politician of the Albanian Party of Labour (PPSh). Life Dume was born in 1920 in Starje, a village in Kolonjë District. During the Second Worl...

Синелобый амазон Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:ЗавропсидыКласс:Пт�...

Strabane ambushPart of the Troubles and Operation BannerNear the ambush siteDate23 February 1985LocationStrabane, County TyroneNorthern Ireland54°49′48″N 7°28′12″W / 54.83000°N 7.47000°W / 54.83000; -7.47000Result British victoryBelligerents Provisional IRAIRA West Tyrone Brigade United Kingdom British Army (SAS)Commanders and leaders Charles BreslinStrength 3 IRA Volunteers 8 soldiersCasualties and losses 3 killed Noneclass=notpageimage| Ambush at S...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

Geometrical concept Not to be confused with cross section (drawing). A cross-section view of a compression seal In geometry and science, a cross section is the non-empty intersection of a solid body in three-dimensional space with a plane, or the analog in higher-dimensional spaces. Cutting an object into slices creates many parallel cross-sections. The boundary of a cross-section in three-dimensional space that is parallel to two of the axes, that is, parallel to the plane determined by thes...

Questa voce o sezione sugli argomenti storia e guerra è priva o carente di note e riferimenti bibliografici puntuali. Sebbene vi siano una bibliografia e/o dei collegamenti esterni, manca la contestualizzazione delle fonti con note a piè di pagina o altri riferimenti precisi che indichino puntualmente la provenienza delle informazioni. Puoi migliorare questa voce citando le fonti più precisamente. Segui i suggerimenti dei progetti di riferimento 1, 2. Guerra di Coreaparte della Guerr...

The Sandman: Dream CountryCover of The Sandman: Dream Country (1991), trade paperback collected edition, art by Dave McKeanPublisherDC ComicsPublication dateJuly–October 1990Title(s)The Sandman #17–20Main character(s)DreamISBNISBN 1-85286-441-9Creative teamWriter(s)Neil Gaiman with material from William ShakespeareArtist(s)Kelley JonesCharles Vess Colleen DoranDave McKeanMalcolm Jones IIIRobbie BuschSteve OliffPenciller(s)Kelley JonesCharles Vess Colleen DoranInker(s)Malcolm Jo...

Сельское поселение России (МО 2-го уровня)Новотитаровское сельское поселение Флаг[d] Герб 45°14′09″ с. ш. 38°58′16″ в. д.HGЯO Страна Россия Субъект РФ Краснодарский край Район Динской Включает 4 населённых пункта Адм. центр Новотитаровская Глава сельского пос�...

馬哈茂德·艾哈迈迪-内贾德محمود احمدینژاد第6任伊朗總統任期2005年8月3日—2013年8月3日副总统帷爾維茲·達烏迪穆罕默德-禮薩·拉希米领袖阿里·哈梅內伊前任穆罕默德·哈塔米继任哈桑·魯哈尼不结盟运动秘书长任期2012年8月30日—2013年8月3日前任穆罕默德·穆尔西继任哈桑·魯哈尼德黑蘭市長任期2003年6月20日—2005年8月3日副职阿里·賽義德盧前任哈桑·馬利克邁達尼�...

1993 studio album by Guns N' Roses Not to be confused with The Linguini Incident. The Spaghetti Incident?Studio album of cover songs by Guns N' RosesReleasedNovember 23, 1993Recorded1990–1993Studio A&M Studios Record Plant Studios Rumbo Recorders Can-Am Recorders Sound Techniques Triad Studios Conway Recording Studios Ocean Way Recording (Los Angeles)[citation needed] Genre Hard rock[1] punk rock[1][2] Length46:03LabelGeffenProducer Mike Clink Gun...

ヨハネス12世 第130代 ローマ教皇 教皇就任 955年12月16日教皇離任 964年5月14日先代 アガペトゥス2世次代 レオ8世個人情報出生 937年スポレート公国(中部イタリア)スポレート死去 964年5月14日 教皇領、ローマ原国籍 スポレート公国親 父アルベリーコ2世(スポレート公)、母アルダその他のヨハネステンプレートを表示 ヨハネス12世(Ioannes XII、937年 - 964年5月14日)は、ロ...

ヨハネス12世 第130代 ローマ教皇 教皇就任 955年12月16日教皇離任 964年5月14日先代 アガペトゥス2世次代 レオ8世個人情報出生 937年スポレート公国(中部イタリア)スポレート死去 964年5月14日 教皇領、ローマ原国籍 スポレート公国親 父アルベリーコ2世(スポレート公)、母アルダその他のヨハネステンプレートを表示 ヨハネス12世(Ioannes XII、937年 - 964年5月14日)は、ロ...

بورت دو شارنتونPorte de Charenton (بالفرنسية) معلومات عامةالتقسيم الإداري الدائرة الثانية عشرة في باريس البلد فرنسا شبكة المواصلات مترو باريس المالك الهيئة المستقلة للنقل في باريس الإدارة الهيئة المستقلة للنقل في باريس الخطوط الخط 8 لمترو باريس المحطات المجاورة بورت دوريه[1...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

American professional wrestler and manager Jason KnightKnight in 2007Websitehttps://assaultchampionshipwrestling.com/Professional wrestling careerRing name(s)Jason[1]Jason Knight[1]Billed height5 ft 9 in (1.75 m)[2]Billed weight224 lb (102 kg)[2]Billed fromEuropeTrained byJohnny Rodz[2]Bobby Bold Eagle[1]DebutJune 1984[2] Jason Knight[2] is a professional wrestler and manager. He is best known for his sti...










![{\displaystyle \mathbb {Q} [i,{\sqrt {3}}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b5cf981a11e866f341618df1d4e6eea8f7d099c)
![{\displaystyle \mathbb {Q} [{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}]\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ce818b60ab35077f0f0d44c46eaae953c5e1131)