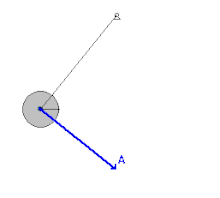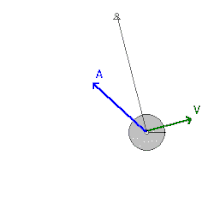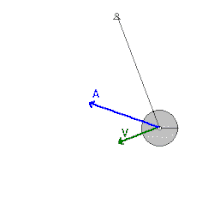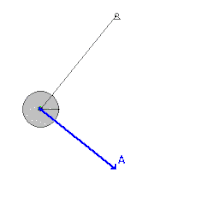
Energia mecânica
|
Read other articles:

Fakultas Teknik Sipil dan LingkunganInstitut Teknologi BandungJenisPerguruan Tinggi Negeri Badan HukumDidirikan1973 (sebagai FTSP)29 Agustus 2005 (sebagai FTSL) DekanIr. Edwan Kardena, Ph.D.LokasiBandung, Jawa Barat, IndonesiaAlamatJl. Ganesha No. 10Bandung 40132Nama julukanFTSL ITBSitus webftsl.itb.ac.id Informasi UmumJenjangS1, S2, S3Jalur MasukSNMPTN, SBMPTN, dan SM ITBGuru Besar Aktif26 orangKelompok Keahlian Rekayasa Struktur Rekayasa Geoteknik Teknik Sumber Daya Air Rekayasa Transportas...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Woodlands, London – news · newspapers · books · scholar · JSTOR (December 2014) (Learn how and when to remove this template message) Human settlement in EnglandWoodlandsSt John the Baptist ChurchWoodlandsLocation within Greater LondonPopulation11,408 (Hou...

Find Me in Your MemoryPoster promosiNama alternatifMemoirs of a Man Memoir of the ManHangul그 남자의 기억법 GenreMelodrama Romansa FantasiDitulis olehKim Yoon-joo Yoon Ji-hyunSutradaraOh Hyun-jong Lee Soo-hyunPemeranKim Dong-wook Moon Ga-youngNegara asalKorea SelatanBahasa asliKoreaJmlh. episode32ProduksiPengaturan kameraSingle-cameraDurasi35 menitRumah produksiChorokbaem MediaDistributorMBCRilis asliJaringanMBC TV NET.Format audioDolby DigitalRilis18 Maret (2020-03-18) –1...

French actress You can help expand this article with text translated from the corresponding article in French. (December 2013) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into th...
Kevin Love Love con la maglia dei Cleveland Cavaliers Nazionalità Stati Uniti Altezza 203 cm Peso 114 kg Pallacanestro Ruolo Ala grande / centro Squadra Miami Heat CarrieraGiovanili Lake Oswego High School2007-2008 UCLA Bruins39 (681)Squadre di club 2008-2014 Minnesota T'wolves364 (6.989)2014-2023 Cleveland Cavaliers489 (7.663)2023- Miami Heat76 (647)Nazionale 2010-2012 Stati Uniti22 (163)Palmarès Olimpiadi Oro Londra 2012 Mondiali Oro Turchia 20...

Disambiguazione – Se stai cercando altri significati, vedi Patroclo (disambigua). PatrocloPatroclo in un affresco nella Casa del Poeta Tragico a Pompei SagaCiclo Troiano Nome orig.Πάτροκλος o Πατροκλῆς (Pátroklos o Patroklễs) Lingua orig.Greco antico AutoreOmero 1ª app. inIliade di Omero Caratteristiche immaginarieEpitetoMeneziade (patronimico) Specieumano Sessomaschio Luogo di nascitaOpunte ProfessioneGuerriero Lotta fra troiani e greci per il corpo di...

Dissident Republican activists in 1884 This article is about dissident 1884 US Republicans. For other uses, see Mugwump (disambiguation). Mugwumps LeaderHenry AdamsEdward AtkinsonCharles Francis Adams Jr.Founded1884Dissolvedc. 1894Split fromRepublican Party Half-Breed faction Preceded byLiberal Republican PartyHalf-Breed faction of the Republican PartyMerged intoDemocratic PartyRepublican PartyIdeologyAnti-corruptionClassical liberalismLiberalismPro-civil service reformPro-Clev...
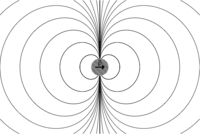
Ne doit pas être confondu avec Dipôle électrique. Schéma du dipôle le plus simple qui soit, produit par deux charges électriques opposées Un dipôle électrostatique se définit par une répartition de charges électriques de somme nulle telles que le barycentre des charges positives ne coïncide pas avec celui des charges négatives. Le dipôle le plus simple est donc un couple de deux charges de signe opposé distantes d'une longueur a non nulle quelconque. Cette notion est principa...

American physician and gynecologist (1813-1883) J. Marion SimsJ. Marion Sims, engraving after photograph, ca. 1880BornJames Marion SimsJanuary 25, 1813 (1813-01-25)[1]Lancaster County, South Carolina, U.S.DiedNovember 13, 1883 (1883-11-14) (aged 70)[2]New York City, U.S.Resting placeGreen-Wood Cemetery, Brooklyn, New York, U.S.EducationSouth Carolina CollegeMedical College of CharlestonAlma materJefferson Medical CollegeOccupationSurgeonKnown forvesico...

1979 book by Peter Singer For the topic of practical ethics, see Applied ethics. Practical Ethics Cover of the 1980 editionAuthorPeter SingerLanguageEnglishSubjectEthicsPublisherCambridge University PressPublication date1979 (first edition)1993 (second edition)2011 (third edition)Publication placeUnited StatesMedia typePrint (hardcover and paperback)Pages395 (second edition)ISBN0-521-43971-X (second edition paperback) Practical Ethics, a 1979 book by the moral philosopher Peter Singer, i...

This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: UK Theatre – news · newspapers · books · scholar · JSTOR (June 2009) (Learn how and when to remove this mes...

معركة صرين (يونيو–يوليو 2015) جزء من الحرب الأهلية السورية،النزاع الكردي السوري–الإسلامي (2013–الآن)، والتدخل في سوريا بقيادة الولايات المتحدة تقدم وحدات حماية الشعب خلال المعركة معلومات عامة التاريخ 18 يونيو 2015 (2015-06-18) – 27 يوليو 2015 (2015-07-27) (شهرًا واحدًا و9 أيامٍ...

保罗·萨缪尔森 Paul Samuelson出生(1915-05-15)1915年5月15日 美国印第安纳州加里逝世2009年12月13日(2009歲—12—13)(94歲) 美国马萨诸塞州贝尔蒙特国籍 美国母校哈佛大学(Ph.D.)芝加哥大学(B.A.)知名于新古典综合 数理经济学经济学方法顯示性偏好理论国际贸易理论经济增长理论公共财产理论奖项约翰·贝茨·克拉克奖(1947)诺贝尔经济学奖(1970)科学生涯研究领域�...

楽天グループ > 楽天カード > 楽天インシュアランスホールディングス 楽天インシュアランスホールディングス株式会社Rakuten Insurance Holdings Co., Ltd. 本社の入居する新宿イーストサイドスクエア種類 株式会社機関設計 監査役会設置会社[1]市場情報 非上場略称 楽天INSHD本社所在地 日本〒101-0053東京都新宿区新宿6-27-30新宿イーストサイドスクエア16階設立 20...

2008年夏季奧林匹克運動會舉重比赛男子女子56公斤級48公斤級62公斤級53公斤級69公斤級58公斤級77公斤級63公斤級85公斤級69公斤級94公斤級75公斤級105公斤級75公斤級以上105公斤級以上查论编 2008年第29届奥林匹克运动会举重比赛于8月9日至19日在北京航空航天大学体育馆举行。本届奥运会该项目共设置15个小项,有86国家参赛,比赛结果共有18个国家、地区代表队获得奖牌,中国获...

Pekan Olahraga Nasional XVIII 2012Tuan rumahPekanbaru, RiauMotoSportivitas untuk KualitasJumlah atlet11.276 [1]Jumlah disiplin43 Cabang OlahragaUpacara pembukaan11 September 2012Upacara penutupan20 September 2012Dibuka olehSoesilo Bambang Yudhoyono[2]Presiden Republik IndonesiaJanji atletBarry AgustiniPenyalaan oborZamri BachtiarTempat utamaStadion Utama Riau← Samarinda XVII Bandung XIX → Pekan Olahraga Nasional XVIII diselenggarakan di Pekanbaru, Riau pada tanggal...

Reserve units of the Australian Army Australian Army ReserveOfficial names:Citizen Military Forces (CMF); (1901–1980) Militia (1929–1943) CMF (1943–1980) Army Reserve (1980–)Active1 March 1901 (as CMF)Country AustraliaTypeMilitiaSize15,596 (Active Reserve)(2022)[1] 12,496 (Standby Reserve)(2009)Part ofAustralian ArmyEngagementsWorld War IWorld War IIEast TimorWar in AfghanistanCommandersChief of ArmyLieutenant General Simon StuartCommander 2nd DivisionMajor General David ...

Questa voce è orfana, ovvero priva di collegamenti in entrata da altre voci. Inseriscine almeno uno pertinente e utile e rimuovi l'avviso. Segui i suggerimenti del progetto di riferimento. Ferrania EuraUna Eura con il logo di Ferrania utilizzato dopo l'acquisizione da parte di 3M, nel 1964TipoCompatta medio formato Formato6 x 6 Pellicola120 Modalitàmanuale Mirinogalileiano Otturatorefisso a 1/50(circa) Tempif/8, f/12 Esposizioni multiplepossibili Flash integratono La Ferrania Eura è una m...

「関西福祉科学大学」とは異なります。 関西福祉大学 関西福祉大学3号館大学設置/創立 1997年学校種別 私立設置者 学校法人関西金光学園本部所在地 兵庫県赤穂市新田380-3北緯34度45分43秒 東経134度22分4.2秒 / 北緯34.76194度 東経134.367833度 / 34.76194; 134.367833座標: 北緯34度45分43秒 東経134度22分4.2秒 / 北緯34.76194度 東経134.367833度 / 34.76194; 134....

Catholic order of chivalry Not to be confused with the Golden Fleece Award. For the French attempt to unify both branches of the Order of the Golden Fleece, see Order of the Three Golden Fleeces. For a modern Georgian award, see Order of the Golden Fleece (Georgia). Distinguished Order of the Golden FleeceInsigne Orden del Toisón de OroInsigne Ordre de la Toison d'OrOrden vom Goldenen VliesInsignes Ordo Velleris Aurei Full set of Insignia of a knight of the Order of the Golden Fleece of Spai...