Esta é uma lista de algumas fórmulas de cálculo do vetor para trabalhar com sistemas comuns de coordenadas curvilíneas[nt 1].
Conversões de coordenadas
Conversão entre coordenadas cartesianas, cilíndricas e esféricas
|
|
De
|
| Cartesiano
|
Cilíndrico
|
Esférico
|
| Para
|
Cartesiano
|

|

|

|
| Cilíndrico
|

|

|

|
| Esférico
|

|

|

|
Conversões de vetor unitário
Conversão entre vetores unitários em sistemas de coordenadas cartesianas, cilíndricas e esféricas em termos de coordenadas de destino
|
|
Cartesiano
|
Cilíndrico
|
Esférico
|
| Cartesiano
|
não aplicável
|

|

|
| Cilíndrico
|

|
não aplicável
|

|
| Esférico
|

|

|
não aplicável
|
Conversão entre vetores unitários em sistemas de coordenadas cartesianas, cilíndricas e esféricas em termos de coordenadas de "fonte"
|
|
Cartesiano
|
Cilíndrico
|
Esférico
|
| Cartesiano
|
não aplicável
|

|

|
| Cilíndrico
|

|
não aplicável
|

|
| Esférico
|

|

|
não aplicável
|
Fórmula Del
Tabela com o operador del em coordenadas cartesianas, cilíndricas e esféricas
| Operação
|
Coordenadas cartesianas (x, y, z)
|
Coordenadas cilíndricas (ρ, φ, z)
|
Coordenadas esféricas (r, θ, φ), onde  é o polar e θ é o ângulo azimutal α é o polar e θ é o ângulo azimutal α
|
| campo vetorial A
|

|

|

|
| Gradiente ∇f
|

|

|

|
| Divergência ∇ ⋅ A
|

|

|

|
| Rotacional ∇ × A
|

|

|

|
| Operador de Laplace ∇2f ≡ ∆f
|

|

|

|
| Vetor de Laplace ∇2A ≡ ∆A
|

|

|
 }}
}}
|
| Derivada materialα[1] (A ⋅ ∇)B
|

|

|
 }}
}}
|
| tensor divergente ∇ ⋅ T
|

|
![{\displaystyle {\begin{aligned}\left[{\frac {\partial T_{\rho \rho }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \rho }}{\partial \varphi }}+{\frac {\partial T_{z\rho }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \rho }-T_{\varphi \varphi })\right]&{\hat {\boldsymbol {\rho }}}\\+\left[{\frac {\partial T_{\rho \varphi }}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {\partial T_{z\varphi }}{\partial z}}+{\frac {1}{\rho }}(T_{\rho \varphi }+T_{\varphi \rho })\right]&{\hat {\boldsymbol {\varphi }}}\\+\left[{\frac {\partial T_{\rho z}}{\partial \rho }}+{\frac {1}{\rho }}{\frac {\partial T_{\varphi z}}{\partial \varphi }}+{\frac {\partial T_{zz}}{\partial z}}+{\frac {T_{\rho z}}{\rho }}\right]&{\hat {\mathbf {z} }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3116bd7e75151c8d599b5e090d2433daffa21069)
|
![{\displaystyle {\begin{aligned}\left[{\frac {\partial T_{rr}}{\partial r}}+2{\frac {T_{rr}}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta r}}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta r}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi r}}{\partial \varphi }}-{\frac {1}{r}}(T_{\theta \theta }+T_{\varphi \varphi })\right]&{\hat {\mathbf {r} }}\\+\left[{\frac {\partial T_{r\theta }}{\partial r}}+2{\frac {T_{r\theta }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \theta }}{\partial \theta }}+{\frac {\cot \theta }{r}}T_{\theta \theta }+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \theta }}{\partial \varphi }}+{\frac {T_{\theta r}}{r}}-{\frac {\cot \theta }{r}}T_{\varphi \varphi }\right]&{\hat {\boldsymbol {\theta }}}\\+\left[{\frac {\partial T_{r\varphi }}{\partial r}}+2{\frac {T_{r\varphi }}{r}}+{\frac {1}{r}}{\frac {\partial T_{\theta \varphi }}{\partial \theta }}+{\frac {1}{r\sin \theta }}{\frac {\partial T_{\varphi \varphi }}{\partial \varphi }}+{\frac {T_{\varphi r}}{r}}+{\frac {\cot \theta }{r}}(T_{\theta \varphi }+T_{\varphi \theta })\right]&{\hat {\boldsymbol {\varphi }}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89522d9531233ee5f0a581ec441bb20c337a13b8)
|
| Deslocamento diferencial dℓ
|

|

|

|
| Área normal diferencial dS
|

|

|

|
| Volume diferencialdV
|

|

|

|
- ↑α Esta página usa
 para o ângulo polar e
para o ângulo polar e  para o ângulo azimutal, que é uma notação comum na física. A fonte que é usada para essas fórmulas usa
para o ângulo azimutal, que é uma notação comum na física. A fonte que é usada para essas fórmulas usa  para o ângulo azimutal e
para o ângulo azimutal e  para o ângulo polar, que é uma notação matemática comum. Para obter as fórmulas de matemática, altere
para o ângulo polar, que é uma notação matemática comum. Para obter as fórmulas de matemática, altere  e
e  nas fórmulas mostradas na tabela acima.
nas fórmulas mostradas na tabela acima.
Regras de cálculo não triviais



 (Fórmula de Lagrange para del)
(Fórmula de Lagrange para del)
Derivação cartesiana
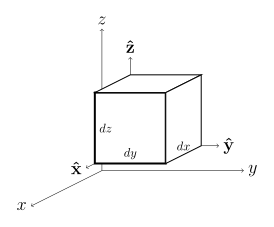


As expressões para  e
e  são encontradas da mesma maneira.[nt 2]
são encontradas da mesma maneira.[nt 2]
Derivação cilíndrica






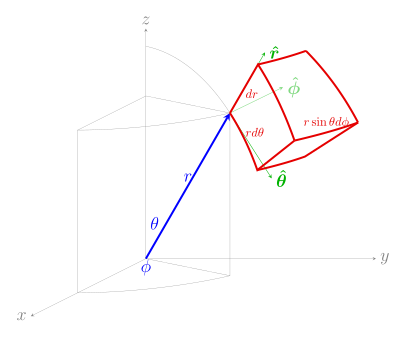
Derivação esférica





Notas
- ↑ Este artigo usa a notação padrão ISO 80000-2, que substitui a ISO 31-11, para coordenadas esféricas (outras fontes podem reverter as definições de θ e φ):
- O ângulo polar é denotado por θ: é o ângulo entre o eixo z e o vetor radial que liga a origem ao ponto em questão.
- O ângulo azimutal é denotado por φ: é o ângulo entre o eixo x e a projeção do vetor radial no plano xy.
A função atan2 (y, x) pode ser usada em vez da função matemática arctan (y/x) devido ao seu domínio e imagem. A função arctan clássica possui uma imagem de (−π/2, +π/2), enquanto que atan2 é definido como tendo uma imagem de (−π, π).
- ↑ "curl" querer dizer "Rotacional"
Referências