Divergência
|
Read other articles:

Api yang terbuat dari briket arang Bahan bakar padat adalah mengacu pada berbagai bentuk bahan padat yang dapat dibakar untuk melepaskan energi, memberikan panas dan cahaya melalui proses pembakaran. Bahan bakar padat dapat dibandingkan dengan bahan bakar cair dan bahan bakar gas. Contoh umum bahan bakar padat termasuk kayu, arang, gambut, batu bara, tablet bahan bakar Heksamin, pelet kayu, jagung, gandum, gandum hitam, dan biji-bijian lainnya. Bahan bakar padat banyak digunakan dalam peroket...

Pour les articles homonymes, voir Drumont (homonymie). Edouard Drumont Drumont, histoire d'un antisémite français est un téléfilm français réalisé par Emmanuel Bourdieu. Synopsis Portrait d'Édouard Drumont, journaliste, qui publie en 1886 La France juive puis fonde le journal La Libre Parole. Il est l'un des propagateurs de l'antisémitisme en France. Diffusion Le téléfilm a été diffusé pour la première fois le 19 mars 2013 sur France 2 ; il a recueilli 5 % de parts d...

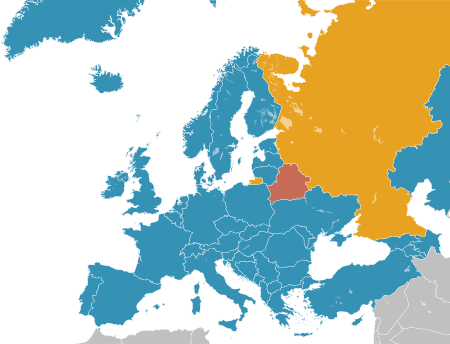
العلاقات الأوكرانية البرازيلية أوكرانيا البرازيل أوكرانيا البرازيل تعديل مصدري - تعديل العلاقات الأوكرانية البرازيلية هي العلاقات الثنائية التي تجمع بين أوكرانيا والبرازيل.[1][2][3][4][5] مقارنة بين البلدين هذه مقارنة عامة ومرجعية للدو�...

Ne doit pas être confondu avec Quenouille. Pour les articles homonymes, voir Fuseau. Dentellière travaillant la dentelle aux fuseaux. Le fuseau est un bâton en bois, renflé à une extrémité ou en son centre, qui permet le filage de la laine, du lin, du chanvre ou du coton. Histoire Le fuseau est une invention très précoce et qui se retrouve suivant des modes proches dans différentes civilisations. Le principe étant une tige qui sert d'axe de rotation comprenant différents « ...

Award for victors of the FIFA World Cup FIFA World Cup TrophyFIFA World Cup TrophyAwarded forWinning the FIFA World CupPresented byFIFAHistoryFirst award1930 (Jules Rimet Trophy) 1974 (FIFA World Cup Trophy)First winner Uruguay (Jules Rimet Trophy, 1930) West Germany (FIFA World Cup Trophy, 1974) Most wins Brazil (5 times)Most recent Argentina (3rd title, 2022)Websitefifa.com The FIFA World Cup is a solid gold trophy that is awarded to the winners of the FIFA World Cup a...

Government agency United States Trade and Development AgencyAgency overviewFormed1992; 32 years ago (1992)Headquarters1101 Wilson Blvd. Arlington, VAEmployees80[1]Annual budget$79.5 million (FY 2021) [2]Agency executiveEnoh Ebong[3], DirectorWebsiteustda.gov The U.S. Trade and Development Agency (USTDA) is an independent agency of the United States government, formed in 1992 to advance economic development and U.S. commercial interests in developing a...

English footballer For the British cyclist, see Adam Yates. Adam Yates Yates as a Port Vale player in September 2010.Personal informationFull name Adam Paul Yates[1]Date of birth (1983-05-28) 28 May 1983 (age 40)[2]Place of birth Werrington, Staffordshire, EnglandHeight 5 ft 10 in (1.78 m)[2]Position(s) Right-backYouth career1992–2002 Crewe AlexandraSenior career*Years Team Apps (Gls)2002–2004 Crewe Alexandra 0 (0)2003–2004 → Halifax Town (l...

Taman Air MunsuLokasiPyongyang, Korea UtaraKoordinat39°02′23″N 125°46′52″E / 39.0396°N 125.7812°E / 39.0396; 125.7812Koordinat: 39°02′23″N 125°46′52″E / 39.0396°N 125.7812°E / 39.0396; 125.7812DibukaNovember 2013 (2013-11)Luas15 hektare (37 ekar)Kolamdalam ruangan dan luar ruanganPerosotan air6 luar ruangan, 2 dalam ruangan Taman Air Munsu Taman Air Munsu (bahasa Korea: 문수물놀이장) adalah sebuah taman air...

شاهنواز بوتو معلومات شخصية الميلاد 21 نوفمبر 1958 كراتشي الوفاة 18 يوليو 1985 (26 سنة) كان مواطنة باكستان الأب ذو الفقار علي بوتو الأم نصرت بوتو إخوة وأخوات مرتضى بوتو، وبينظير بوتو الحياة العملية المهنة سياسي الحزب حزب الشعب الباكستاني اللغة...

Constituency in Seoul, South Korea Yeongdeungpo ASingle-member constituencyfor the National AssemblyLocation of the constituencyDistrict(s)Yeongdeungpo District (part)RegionSeoulElectorate187,997 (2020)Current constituencyCreated1988Seats1PartyDemocratic PartyMember(s)Chae Hyeon-ilCreated fromYeongdeungpo Yeongdeungpo A (Korean: 영등포구 갑) is a constituency of the National Assembly of South Korea. The constituency consists of portions of Yeongdeungpo District, Seoul. As of 202...

This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Fiat 128 SOHC engine – news · newspapers · books · scholar · JSTOR (November 2011) (Learn how and when to remove this message) Reciprocating internal combustion engine Fiat SOHC engineOverviewManufacturerFiatLanciaZastava AutomobilesTofaşAlso calledFiat Torque...

Junee BushfireDate(s)1 January 2006 (2006-01-01) – 6 January 2006 (2006-01-06)LocationJunee, New South Wales, AustraliaCoordinates34°51′52″S 147°30′01″E / 34.86444°S 147.50028°E / -34.86444; 147.50028StatisticsBurned areaMore than 25,200 hectares (62,000 acres)[1]Land useResidentialFarmlandForest reservesImpactsNon-fatal injuries1[2]Structures destroyed14+[1] — 10 houses — 4 shearing sheds — num...

Synagogue in Manhattan, New York Kehila Kedosha JaninaKehila Kedosha Janina synagogue in 2007ReligionAffiliationJudaismRiteRomanioteEcclesiastical or organizational statusSynagogueLeadershipLay ledStatusActiveLocationLocation280 Broome Street, Manhattan, New York City, New YorkCountryUnited StatesLocation in Lower ManhattanGeographic coordinates40°43′7″N 73°59′28″W / 40.71861°N 73.99111°W / 40.71861; -73.99111ArchitectureArchitect(s)Sydney DaubTypeSynagogue...

Commune in Provence-Alpes-Côte d'Azur, France You can help expand this article with text translated from the corresponding article in French. (December 2008) Click [show] for important translation instructions. View a machine-translated version of the French article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pastin...

Serbian medieval dynasty VojislavljevićВојислављевићRoyal houseCountryDuklja/Doclea (modern Montenegro, Herzegovina, southernmost Dalmatia)Founded1018FounderStefan VojislavFinal rulerMihailo III of DukljaTitles Prince (archon) Grand Prince (1050–1077) King of Slavs (rex Sclavorum; 1077–1080) Prince of Serbs,[1] of Serbia[2] Dissolution1189Cadet branchesVukanović dynasty–Nemanjić dynasty The House of Vojislavljević (Serbian Cyrillic: Војиславље...

Cet article est une ébauche concernant les amphibiens. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations du projet Herpétologie. Crinia signifera Classification ASW Règne Animalia Embranchement Chordata Sous-embr. Vertebrata Classe Amphibia Sous-classe Lissamphibia Super-ordre Salientia Ordre Anura Sous-ordre Neobatrachia Famille Myobatrachidae Genre Crinia EspèceCrinia signiferaGirard, 1853 Synonymes Camariolius varius Peters, 1863 Pter...
La peine de mort dans le monde Abolie pour tous les crimes Abolie pour tous les crimes sauf quelques exceptions Légale mais non appliquée Légale et appliquée Cette section a besoin d'être recyclée (juillet 2023). Une réorganisation et une clarification du contenu sont nécessaires. Améliorez-la ou discutez des points à améliorer. L'application de la peine de mort dans le monde est pratiquée par plusieurs États de tous les continents, mais la plupart l'ont abolie en droit ou e...

Historically, the main residence of the lord of the manor This article is about a type of historical building. For other uses, see Manor house (disambiguation). This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages) This article's lead section may be too short to adequately summarize the key points. Please consider expanding the lead to provide an accessible overview of all important aspects of the artic...

Caribbean island shared by the Dominican Republic and Haiti Isla Española and San Domingo redirect here. For the Galápagos island, see Española Island. For other uses, see San Domingo (disambiguation). La Española La Española (Spanish) Hispaniola (French) Ispayola (Haitian Creole) Ayití, Bohío, Babeque (Taino) Quisqueya (Ciguayo) View from the ISS, 2011GeographyLocationCaribbean SeaCoordinates19°N 71°W / 19°N 71°W / 19; -71ArchipelagoGrea...

أواك هيل الإحداثيات 39°14′47″N 97°20′32″W / 39.2464°N 97.3422°W / 39.2464; -97.3422 [1] تقسيم إداري البلد الولايات المتحدة[2] التقسيم الأعلى مقاطعة كلاي خصائص جغرافية المساحة 0.12205 كيلومتر مربع (1 أبريل 2010) ارتفاع 387 متر عدد السكان عدد السكان 24 (1 أ...





















![{\displaystyle \Delta {\dot {m}}_{\Delta y\Delta z}=[{{\overrightarrow {J}}(x+\Delta x,y,z)\ -}{{\overrightarrow {J}}(x,y,z)]\cdot {{\overrightarrow {A}}_{\Delta y\Delta z}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d029871d09aa3c895b1384310398c1fac644cca)


![{\displaystyle \Delta {\dot {m}}_{\Delta y\Delta z}=[{J_{1}(x+\Delta x,y,z)\ -}{J_{1}(x,y,z)]\Delta y\Delta z}=(\Delta J_{1})\Delta y\Delta z}](https://wikimedia.org/api/rest_v1/media/math/render/svg/155a812dc427badbfcdd95fdff534113fe0060f8)


















![{\displaystyle \operatorname {div} \,\mathbf {F} ={\frac {1}{h_{1}h_{2}h_{3}}}\left[{\frac {\partial }{\partial q_{1}}}\left(h_{2}h_{3}F_{1}\right)+{\frac {\partial }{\partial q_{2}}}\left(h_{1}h_{3}F_{2}\right)+{\frac {\partial }{\partial q_{3}}}\left(h_{1}h_{2}F_{3}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8a7160d2bbdfbbcb949516d036f21b8cdf92ef4)







