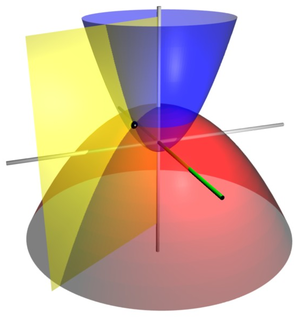
Coordenadas parabólicas
|
Read other articles:

Artikel ini sebatang kara, artinya tidak ada artikel lain yang memiliki pranala balik ke halaman ini.Bantulah menambah pranala ke artikel ini dari artikel yang berhubungan atau coba peralatan pencari pranala.Tag ini diberikan pada November 2022. John BrownLahir(1810-09-22)22 September 1810Biggar, Lanarkshire Selatan, SkotlandiaMeninggal11 Mei 1882(1882-05-11) (umur 71)Edinburgh, SkotlandiaKebangsaanSkotlandiaPekerjaandokter, esayis John Brown 23 Rutland Street, Edinburgh Makam Dr John Br...

Percussion instrument played to produce sounds of indeterminate pitch A pair of timbales, two cowbells, a jam block and a cymbal all in use as unpitched percussion Three instruments on the spectrum between pitched and unpitched: whistle, woodblocks, crotales Playⓘ An unpitched percussion instrument is a percussion instrument played in such a way as to produce sounds of indeterminate pitch, or an instrument normally played in this fashion. Unpitched percussion is typically used to maintain a...

Public law schoolFaculty of Law, University of IndonesiaLocationDepok, West Java, IndonesiaInformationSchool typePublic law schoolEstablished1909 – 18 May 1928 (as Rechtsschool) 28 October 1924; 99 years ago (1924-10-28) (as Rechtshogeschool) 21 June 1946; 77 years ago (1946-06-21) (as Nood Universiteit) 1950; 74 years ago (1950) (as Universiteit Indonesia)DeanParulian Paidi AritonangFaculty1Enrollment485 (2022)Websitelaw.ui.ac.id The Fa...

Place in Jammu and Kashmir, Jammu & KashmirAchabal AchivalAchabal TownAchabalLocation in Jammu and Kashmir, IndiaShow map of Jammu and KashmirAchabalAchabal (India)Show map of IndiaCoordinates: 33°41′N 75°14′E / 33.68°N 75.23°E / 33.68; 75.23CountryJammu & KashmirUnion territoryJammu and KashmirDistrictAnantnagElevation1,936 m (6,352 ft)Population (2001) • Total5,835Languages • OfficialKashmiri, Urdu, Hindi, Dogri...

Championnat d'Asie du Sud-Est de football 2022 Généralités Sport Football Organisateur(s) AFF Éditions 14e Lieu(x) ASEAN Date du 20 décembre 2022au 16 janvier 2023 Participants 10 équipes (+1 en qualifications) Matchs joués 26 rencontres Affluence 479 571 (18 445 par match) Site(s) 10 stades Site web officiel AFF Mitsubishi Electric Cup Site officiel Palmarès Tenant du titre Thaïlande (6) Vainqueur Thaïlande (7e titre) Finaliste Viêt Nam Demi-finalistes Malaisie...

Family of bivalves This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Anomiidae – news · newspapers · books · scholar · JSTOR (February 2017) (Learn how and when to remove this template message) Anomiidae Two beach-worn shells of Anomia ephippium Scientific classification Domain: Eukaryota Kingdom: Animalia Phy...

Lembaga Penerbangan dan Antariksa Nasional LAPANGambaran umumDidirikan27 November 1963; 60 tahun lalu (1963-11-27)Dasar hukum UU No. 21 Tahun 2013 tentang Keantariksaan Perpres No. 49 Tahun 2015 tentang LAPAN DibubarkanSeptember 2021; 2 tahun lalu (2021-09)Nomenklatur penggantiOrganisasi Riset Penerbangan dan Antariksa di bawah Badan Riset dan Inovasi NasionalBidang tugasPenerbangan dan antariksaSloganLAPAN Unggul Indonesia Maju, LAPAN Melayani Indonesia Mandiri[1]Pegawai1.2...

Upcoming Namma Metro station under Yellow Line Ragigudda Namma Metro stationFinal stages of this metro station under Namma MetroGeneral informationLocation45th Cross, Marenahalli, 5th Block, Jayanagar, Bengaluru, Karnataka 560041Coordinates12°55′02″N 77°35′18″E / 12.91711°N 77.58837°E / 12.91711; 77.58837Owned byBangalore Metro Rail Corporation Ltd (BMRCL)Operated byNamma MetroLine(s)Yellow LinePlatformsSide platformPlatform-1 → Rashtreeya Vidyalaya RoadP...

Peta menunjukkan lokasi Toboso Toboso adalah munisipalitas yang terletak di provinsi Negros Occidental, Filipina. Pada tahun 2010, munisipalitas ini memiliki populasi sebesar 41.954 jiwa dan 8.275 rumah tangga. Pembagian wilayah Secara administratif Toboso terbagi menjadi 9 barangay, yaitu: Bandila Bug-ang General Luna Magticol Poblacion Salamanca San Isidro San Jose Tabun-ac Pranala luar Philippine Standard Geographic Code Diarsipkan 2012-04-13 di Wayback Machine. 1995 Philippine Census Info...

Canadian Press's lead war correspondent (1913 - 1990) For the Scottish footballer, see Ross Munro (footballer). Canadian Press war correspondent Ross Munro typing a story in the battle area between Valguarnera and Leonforte, Italy, August 1943 Robert Ross Munro, OBE, OC (September 6, 1913 - June 21, 1990) was the Canadian Press's lead war correspondent in Europe in World War II. He covered a Canadian raid in Spitsbergen, the 1942 raid on Dieppe, the Allied landings in Sicily, the Italian camp...

Communication network Top of a cellular radio tower Indoor cell site in Germany Part of a series onAntennas Common types Dipole Fractal Loop Monopole Satellite dish Television Whip Components Balun Block upconverter Coaxial cable Counterpoise (ground system) Feed Feed line Low-noise block downconverter Passive radiator Receiver Rotator Stub Transmitter Tuner Twin-lead Systems Antenna farm Amateur radio Cellular network Hotspot Municipal wireless network Radio Radio masts and towers Wi-Fi Wire...

ХристианствоБиблия Ветхий Завет Новый Завет Евангелие Десять заповедей Нагорная проповедь Апокрифы Бог, Троица Бог Отец Иисус Христос Святой Дух История христианства Апостолы Хронология христианства Раннее христианство Гностическое христианство Вселенские соборы Н...

Sydney WaterSydney Water logoInformasi lembagaDibentuk26 Maret 1888Wilayah hukumPemerintah New South WalesKantor pusat1 Smith Street Parramatta, New South Wales, AustraliaMenteriPhillip Costa, Menteri AirPejabat eksekutifKerry Schott, Direktur ManajerTom Parry, Ketua DewanSitus webwww.sydneywater.com.au Sydney Water adalah sebuah perusahan pemerintah New South Wales yang menyediakan layanan air minum, air buangan dan beberapa air badai ke Sydney, Illawarra dan Blue Mountains, di Australia. Sy...

French screenwriter and film director (born 1925) Jean-Charles TacchellaBorn (1925-09-23) 23 September 1925 (age 98)Cherbourg, Manche, Normandy, FranceOccupation(s)Film director, screenwriter, cinematographerYears active1955–2008 Jean-Charles Tacchella (born 23 September 1925) is a French screenwriter and film director. He was nominated for an Academy Award for Best Original Screenplay for his film Cousin Cousine (1975), which was also nominated for the Academy Award for Best Fore...

У этого термина существуют и другие значения, см. Российская империя (значения). ИмперияРоссийская империярус. дореф. Россійская имперія Флаг[~ 1][~ 2] Большой государственный герб Девиз: «Съ нами Богъ!» Гимн: «Молитва русских»(1816—1833)«Боже, Царя храни!»(1833—1917) Тер...

بريبيات Official seal of بريبياتشعار الاسم الرسمي При́п'ять (بالأوكرانية) При́пять (بالروسية) الإحداثيات 51°24′23″N 30°03′27″E / 51.4065°N 30.057472222222°E / 51.4065; 30.057472222222 تاريخ التأسيس 4 فبراير 1970 سبب التسمية نهر بريبيات تقسيم إداري البلد أوكرانيا[2][1] التق�...

هذه المقالة عن طقس مسيحي. لكنيسة بروتستانتية، طالع الكنيسة المعمدانية. المعمودية، وهو سر دخول المرء في المسيحية. المعمودية.المعمودية أو العِماد[1] أو التعميد[1] طقس إدخال وتبنٍّ مسيحي،[2] يكون دائمًا تقريبًا بالماء، ويدخل فيه الإنسان في المسيحية.[3][4...

DiwakarBorn (1990-01-26) 26 January 1990 (age 34)Occupation(s)Playback Singer, Live PerformerYears active2014 to present Dhivagaran Santhosh (also known as Diwakar) is an Indian playback singer and live performer. He is best known for winning Airtel Super Singer 4',[1][2][3] a Tamil language musical reality TV show which was telecast from February 4th 2013 to February 1st 2014 on Vijay TV. Career Television works Diwakar participated in various reality TV mu...

Indian singer Neyyattinkara VasudevanBackground informationBorn1940OriginNeyyattinkara, Kerala, IndiaDied13 May 2008 (aged 68)GenresCarnatic musicOccupation(s)Carnatic ComposerMusical artist Neyyattinkara Vasudevan Sings with Thodupuzha Manojkumar on Violin, Erickavu N. Sunil on Mridangam, and Elanjimel.P.Sushilkumar on Ghatom Neyyattinkara Vasudevan (1940–13 May 2008) was a Carnatic music vocalist from Kerala in south India.[1] The Padmasree-winning Carnatic vocalist and disci...

Astronomical instrument For other pages with a similar name, see Astrolabe (disambiguation). Not to be confused with Cosmolabe. North African, 9th century AD, Planispheric Astrolabe. Khalili Collection. A modern astrolabe made in Tabriz, Iran in 2013. An astrolabe (Greek: ἀστρολάβος astrolábos, 'star-taker'; Arabic: ٱلأَسْطُرلاب al-Asṭurlāb; Persian: ستارهیاب Setāreyāb) is an astronomical instrument dating to ancient times. It serves as a star chart and...
































![{\displaystyle \nabla ^{2}\Phi ={\frac {1}{\sigma ^{2}+\tau ^{2}}}\left[{\frac {1}{\sigma }}{\frac {\partial }{\partial \sigma }}\left(\sigma {\frac {\partial \Phi }{\partial \sigma }}\right)+{\frac {1}{\tau }}{\frac {\partial }{\partial \tau }}\left(\tau {\frac {\partial \Phi }{\partial \tau }}\right)\right]+{\frac {1}{\sigma ^{2}\tau ^{2}}}{\frac {\partial ^{2}\Phi }{\partial \varphi ^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d85f22be17ef06352216921e7073b7ace36a15c)

























