Construção de Cayley-Dickson
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

This article is about the city in Arkansas. For the city in Texas, see Texarkana, Texas. This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Texarkana, Arkansas – news · newspapers · books · scholar · JSTOR (July 2017) (Learn how and when to remove this template message) City in Arkansas, United StatesTexarkana,...

City in Sicily, Italy For other uses, see Noto (disambiguation). You can help expand this article with text translated from the corresponding article in Italian. (January 2022) Click [show] for important translation instructions. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the Engli...

Wakil Bupati Bolaang Mongondow TimurPetahanaOskar Manoppo, S.E., M.M.sejak 26 Februari 2021Masa jabatan5 tahunDibentuk4 Oktober 2010Pejabat pertamaMedy Lensun, S.T.Situs webboltimkab.go.id Berikut ini adalah daftar Wakil Bupati Bolaang Mongondow Timur dari masa ke masa. No Portret Wakil Bupati Mulai Jabatan Akhir Jabatan Prd. Ket. Bupati 1 Medy LensunS.T. 4 Oktober 2010 4 Oktober 2015 1 Sehan Salim LandjarS.H. Jabatan kosong 5 Oktober 2015 17 Februari 2016 - Muhammad Rudi M...
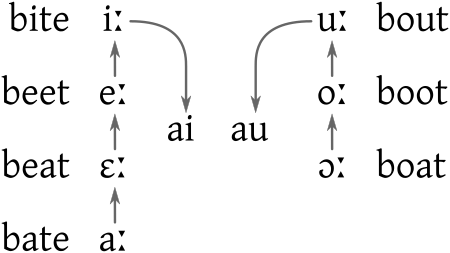
Pour la police de caractères, voir Dyslexie (police de caractères). Dyslexie On parle de dyslexie pour distinguer le trouble de la lecture en général et plus récemment un trouble spécifique de l'apprentissage de la lecture qui tend à être rapporté à une cause physiologique[1]. Données clés Causes Maladie génétique Symptômes Trouble de la lecture Traitement Spécialité Neuropsychologie et pédiatrie Classification et ressources externes CISP-2 P24 CIM-10 R48.0 CIM-9 315.02 OMI...

Questa voce sull'argomento stagioni delle società calcistiche italiane è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Voce principale: Associazione Calcio Pisa 1909. Pisa Sporting ClubStagione 1922-1923Sport calcio Squadra Pisa Allenatore József Ging Presidente Giacomo Picchiotti Prima Divisione4º posto nel girone A della Lega Nord. Maggiori presenzeCampionato: Colombari (21) Miglior marcatore...

Artikel ini bukan tentang cendekiawan klasik Michael Winterbottom (akademisi). Michael WinterbottomMichael Winterbottom, 2009Lahir29 Maret 1961 (umur 63)Blackburn, Lancashire, Inggris, Britania RayaPekerjaanSutradara Michael Winterbottom (lahir 29 Maret 1961) adalah seorang pembuat film asal Inggris. Ia memulai kariernya dengan berkarya dalam televisi Britania Raya sebelum beralih ke perfilman fitur. Referensi dan catatan Pranala luar Wikimedia Commons memiliki media mengenai Michael Win...
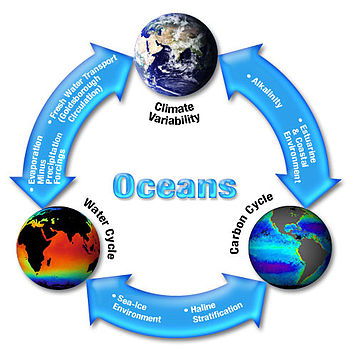
Scientific study of the Earth's spheres and their natural integrated systems An ecological analysis of CO2 in an ecosystem. As systems biology, systems ecology seeks a holistic view of the interactions and transactions within and between biological and ecological systems. Earth system science (ESS) is the application of systems science to the Earth.[1][2][3][4] In particular, it considers interactions and 'feedbacks', through material and energy fluxes, between...

Luxembourgish footballer and manager This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Antoine Kohn – news · newspapers · books · scholar · JSTOR (November 2...

Antifungal chemical compound Ketoconazole(2R,4S)-(+)-ketoconazole (top)(2S,4R)-(−)-ketoconazole (bottom)Ball-and-stick model of (2R,4S)-(+)-ketoconazoleClinical dataPronunciation/ˌkiːtoʊˈkoʊnəˌzoʊl, -zɒl/[1][2] Trade namesNizoral, othersOther namesR-41400; KW-1414AHFS/Drugs.comMonographMedlinePlusa682816License data US DailyMed: Ketoconazole Pregnancycategory AU: B3 Routes ofadministrationBy mouth (tablets), topical (cream, shampoo, solution)ATC ...
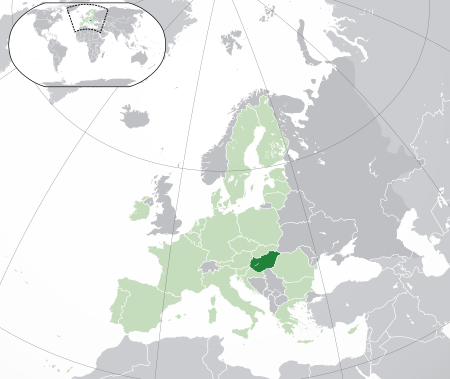
HungariaMagyarország (Hungaria) Bendera Lambang Semboyan: —Lagu kebangsaan: Himnusz (Indonesia: Himne Nasional Hungaria) Perlihatkan BumiPerlihatkan peta EropaPerlihatkan peta BenderaLokasi Hungaria (hijau gelap)– di Eropa (hijau & abu-abu)– di Uni Eropa (hijau)Ibu kota(dan kota terbesar)Budapest47°26′N 19°15′E / 47.433°N 19.250°E / 47.433; 19.250Bahasa resmiHungariaKelompok etnik ...

Indigenous people of southern Iraq Maʻdān redirects here. Not to be confused with Ma'adan. Ethnic group Marsh Arabs ʻArab al-Ahwār عرب الأهوارMarsh Arabs on a boat.Total population6 to 8 millions descendants (based on population in 1950)[1]Regions with significant populations Iraq85,000 (6 million descendants in Governorate of Meysan, Basra and Dhi Qar regions of Mesopotamian Marsh) Iran120,000 (1.6 million with descendants in Khuzestani Marshland and Iraqi ref...

Salah satu masjid di kota Monastir Monastir adalah sebuah kota yang terletak di sebelah timur Tunisia, sekitar 165 km dari ibu kota Tunisia, Tunis. Penduduknya berjumlah 71.546 jiwa (2004). Presiden Tunisia, Habib Bourguiba, lahir di kota ini. Kota ini merupakan ibu kota Governorat Monastir. Kota ini merupakan kota pelabuhan terbesar kelima di Tunisia setelah Tunis, Sfax, Sousse, dan Bizerte. Monastir dijuluki sebagai 'kota pasir' karena musim panasnya yang panjang dan panas. Pranala lua...

Arish atau el-Arīsh (bahasa Arab: العريش ) adalah ibu kota dan kota terbesar (dengan jumlah penduduk 114.900) dari Governorat Shamal Sina', Mesir, yang terletak di pantai laut tengah dan di semenanjung Sinai, 344 kilometer dari Kairo. El Arish selama Perang Enam Hari dan Kontroversi 7 Juni 1967: Tentara Israel mengawal tawanan-tawanan perang Mesir di El Arish (Shabtai Tal). Dalam sebuah pertemuan untuk Radio Israel pada tanggal 16 Agustus 1995, Aryeh Yitzhaki yang dahulu bertugas di Pu...

1956 studio album by Milt JacksonRoll 'Em BagsStudio album by Milt JacksonReleased1956RecordedJanuary 25, 1949 and January 5, 1956StudioNew York City and Van Gelder Studio, Hackensack, NJGenreJazzLength42:21LabelSavoyMG 12042ProducerOzzie CadenaMilt Jackson chronology Wizard of the Vibes(1952) Roll 'Em Bags(1956) Meet Milt Jackson(1956) Roll 'Em Bags is an album by American jazz vibraphonist Milt Jackson featuring performances recorded in 1949 and 1956 and released on the Savoy label....

Branch of criminology involving crimes against the environment A major contributor to this article appears to have a close connection with its subject. It may require cleanup to comply with Wikipedia's content policies, particularly neutral point of view. Please discuss further on the talk page. (April 2014) (Learn how and when to remove this message) Green criminology is a branch of criminology that involves the study of harms and crimes against the environment broadly conceived, including t...

Questa voce sull'argomento cestisti statunitensi è solo un abbozzo. Contribuisci a migliorarla secondo le convenzioni di Wikipedia. Segui i suggerimenti del progetto di riferimento. Tony JarosNazionalità Stati Uniti Altezza191 cm Peso84 kg Pallacanestro RuoloAla piccola / guardia Termine carriera1951 CarrieraGiovanili Edison High School1941-1942 Minnesota Gophers1945-1946 Minnesota Gophers Squadre di club 1946-1947 Chicago Stags591948-1951 Minneapolis Lakers24...

Long, relatively narrow land bounded by distinctly steeper slopes above and below This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Bench geology – news · newspapers · books · scholar · JSTOR (January 2021) (Learn how and when to remove this message) Hypothetical cross-section of a river valley showing di...

List of events ← 1539 1538 1537 1536 1535 1540 in Ireland → 1541 1542 1543 1544 1545 Centuries: 14th 15th 16th 17th 18th Decades: 1520s 1530s 1540s 1550s 1560s See also:Other events of 1540 List of years in Ireland Events from the year 1540 in Ireland. Incumbent Lord: Henry VIII Events Anthony St Leger is appointed Lord Deputy of Ireland and tasked with the repression of disorder, beginning the pacification policy of surrender and regrant (which lasts until 1543).[1] Murr...

Square in the Royal Borough of Kensington and Chelsea View of Ladbroke Square gardens. Ladbroke Square is a garden square in Notting Hill, west London, England.[1][2] Location Ladbroke Square and its gardens lie north of Holland Park Avenue and Notting Hill Gate (part of the A40 road). To the west is Ladbroke Grove (part of the B450 road), to the north is Kensington Park Gardens (with houses on the south side backing onto the gardens), and to the northeast is Kensington Park R...

US Army jungle warfare formation This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: 25th Infantry Division United States – news · newspapers · books · scholar · JSTOR (April 2008) (Learn how and when to remove this message) 25th Infantry DivisionShoulder sleeve insignia of the 25th Infantry Division; the o...











































