Ciências formais
|
Read other articles:

Grand Prix Sepeda Motor F.I.M. musim 2021 Sebelum: 2020 Sesudah: 2022 MotoGP musim 2021Moto2 musim 2021MotoE musim 2021Juara DuniaPembalap: Pedro Acosta (KTM)Pabrikan: KTMTim: Red Bull KTM AjoRookie: Pedro Acosta (KTM) Kejuaraan Dunia FIM Moto3 2021 adalah bagian dari musim Kejuaraan Dunia F.I.M. Road Racing ke-73. Pedro Acosta mengamankan kejuaraan 2021 dengan satu balapan tersisa di musim ini, yang dirusak oleh kematian Jason Dupasquier selama sesi kualifikasi kedua Grand Prix Italia.[...

A Night at the GardenPoster filmSutradaraMarshall CurryProduserMarshall Curry, Laura Poitras, Charlotte CookDitulis olehMarshall CurryPenata musikJames BaxterPenyuntingMarshall CurryDistributorField of VisionTanggal rilis 2017 (2017) (daring) Januari 2018 (2018-01) (Sundance) Durasi7 menitNegaraAmerika SerikatBahasaInggris A Night at The Garden adalah film dokumenter pendek tahun 1939 tentang rapat umum Nazi di Madison Square Garden, New York City, tahun 1939. Film ini...

Berbagai jenis keju dijual di sebuah toko di Lille, Prancis. Keju Prancis adalah segala jenis keju yang diproduksi baik secara modern ataupun tradisional di negara Prancis. Hingga saat ini Prancis memproduksi sekitar 400 jenis keju (fromage dalam bahasa Prancis) yang berbeda.[1] Jumlah ini jauh lebih banyak dibandingkan ketika Charles de Gaulle memerintah di Prancis.[2] Ketika itu variasi keju di Prancis ada sebanyak 246 jenis.[2] Keju-keju tersebut ada yang dibuat dar...

This article contains content that is written like an advertisement. Please help improve it by removing promotional content and inappropriate external links, and by adding encyclopedic content written from a neutral point of view. (January 2018) (Learn how and when to remove this template message) Seven Generations Education InstituteMottoCulturally enriched quality education for allTypeAboriginal-owned and controlled education institutionEstablished1985 as Rainy Lake Ojibway Education Author...
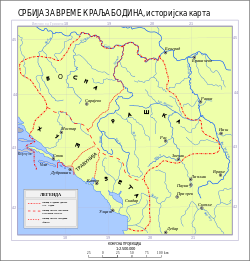
Duklja and neighbouring Serbian regions during the 11th and 12th century For other people with the same name, see Mihailo of Duklja. Mihailo III (Serbian Cyrillic: Михаило) was Prince of Duklja, from c. 1180, or before, up to 1186 or 1189. He was descended from the Vojislavljević dynasty, and also cousin to Grand Prince Stefan Nemanja of Serbia. The Principality of Duklja was tributary to the Byzantine Empire until 1180, when Emperor Manuel I died and Empire plunged into turmoil. By 1...

هذه المقالة بحاجة لمراجعة خبير مختص في مجالها. يرجى من المختصين في مجالها مراجعتها وتطويرها. هذه القائمة غير مكتملة. فضلاً ساهم في تطويرها بإضافة مزيد من المعلومات ولا تنسَ الاستشهاد بمصادر موثوق بها. اختراعات المسلمين قدم العالم الإسلامي العديد من الاختراعات والاكتشافات...

2007 single by CupidCupid ShuffleSingle by Cupidfrom the album Time for a Change ReleasedFebruary 13, 2007RecordedDecember 30, 2006GenreDancehip hopLength3:50LabelAsylum AtlanticSongwriter(s)CupidProducer(s)CupidCupid singles chronology Say Yes (2007) Cupid Shuffle (2007) Happy Dance (2008) Cupid Shuffle is a song by Cupid from his 2007 studio album Time for a Change. It has spawned a popular line dance and has drawn comparisons to DJ Casper's Cha Cha Slide. In the United States, the song pea...

For other battles in the same place, see Battle of Algiers. 2nd Bombardment of AlgiersPart of the Spanish-Algerian war (1775–1785)Algiers' harbour. Engraving from 1690.Date12 July 1784LocationAlgiers, Regency of AlgiersResult Algerian victory[1][2]Belligerents Kingdom of Spain Kingdom of Sicily Order of Malta Kingdom of Naples Kingdom of Portugal Regency of AlgiersCommanders and leaders Antonio Barceló Jose de Mazarredo Muhammad V Ali AghaStrength 9 ships of the line ...

American fashion doll and media franchise This article is about the fashion doll line and media franchise. For people with the surname, see Bratz (surname). For other uses, see Bratz (disambiguation). BratzTypeFashion dollMedia franchiseInventor(s)Carter BryantCompanyMGA EntertainmentCountryUnited StatesAvailability2001 (23 years ago)–presentSloganthe girls with the passion for fashionOfficial website Bratz is an American fashion doll and media franchise created by former Mattel employee Ca...

فولتا سان خوان 2017 تفاصيل السباقسلسلة35. فولتا سان خوانمنافسةطواف أمريكا للدراجات 2017 2.1مراحل7التواريخ23 – 29 يناير 2017المسافات902٫8 كمالبلد الأرجنتيننقطة البدايةسان خوان، الأرجنتيننقطة النهايةسان خوان، الأرجنتينالفرق26عدد المتسابقين في البداية161عدد المتسابقين في النهاي�...

le Semnon Le Semnon entre Pléchâtel et Poligné. Cours du Semnon. Caractéristiques Longueur 73,3 km [1] Bassin 496 km2 [1] Bassin collecteur la Vilaine Débit moyen 2,8 m3/s (Bain-de-Bretagne) Régime pluvial Cours Source source · Localisation Saint-Erblon · Coordonnées 47° 47′ 13″ N, 1° 08′ 25″ O Confluence la Vilaine · Localisation Saint-Senoux · Coordonnées 47° 53′ 57″ N, 1° 45′ 27″ O G...

此條目需要补充更多来源。 (2021年7月4日)请协助補充多方面可靠来源以改善这篇条目,无法查证的内容可能會因為异议提出而被移除。致使用者:请搜索一下条目的标题(来源搜索:美国众议院 — 网页、新闻、书籍、学术、图像),以检查网络上是否存在该主题的更多可靠来源(判定指引)。 美國眾議院 United States House of Representatives第118届美国国会众议院徽章 众议院旗...

American model Heather KozarKozar in 2015Playboy centerfold appearanceJanuary 1998Preceded byKaren McDougalSucceeded byJulia SchultzPlayboy Playmate of the Year1999Preceded byKaren McDougalSucceeded byJodi Ann PatersonPersonal detailsBorn (1976-05-04) May 4, 1976 (age 48)Akron, Ohio, US[1]Height5 ft 8 in (1.73 m)[2] Heather Kozar (born May 4, 1976) is an American glamour model known as Playboy's Playmate of the Month for January 1998 and Playmate of the...

الحزب الاجتماعي للوحدة الوطنية البلد كولومبيا تاريخ التأسيس 18 ديسمبر 2005 المقر الرئيسي بوغوتا الأيديولوجيا طرف خارجي، وليبرالية اجتماعية الموقع الرسمي الموقع الرسمي تعديل مصدري - تعديل الحزب الاجتماعي للوحدة الوطنية (بالإسبانية: Partido Social de Unidad ...

Usenet/newsgroup service provider This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) The topic of this article may not meet Wikipedia's notability guidelines for companies and organizations. Please help to demonstrate the notability of the topic by citing reliable secondary sources that are independent of the topic and provide significant coverage of it beyond a mere trivial mention. If nota...

Chemical compound MinaxoloneClinical dataOther names11α-(Dimethylamino)-2β-ethoxy-3α-hydroxy-5α-pregnan-20-oneATC codenoneIdentifiers IUPAC name 1-[(1S,2S,4S,5S,7S,10S,11S,14S,15S,17R)-17-(dimethylamino)-4-ethoxy-5-hydroxy-2,15-dimethyltetracyclo[8.7.0.02,7.011,15]heptadecan-14-yl]ethan-1-one CAS Number62571-87-3 YPubChem CID71960IUPHAR/BPS5478ChemSpider64967 NUNII737SKC73L0KEGGD05041 YChEMBLChEMBL2105209 NCompTox Dashboard (EPA)DTXSID201024283 Chemical and physical da...
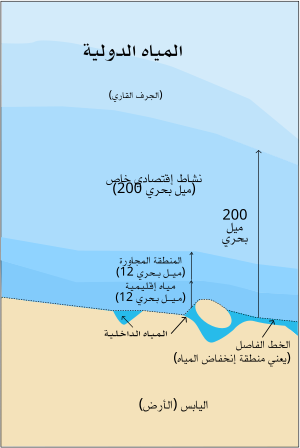
ميّز عن منطقة اقتصادية خاصة. المناطق الاقتصادية الخالصة في العالم موضحة باللون الأزرق الداكن (مميزة عن المياه الدولية باللون الأزرق الفاتح) المنطقة الاقتصادية الخالصة (EEZ)، وفقا لما ما هو منصوص عليه في المادة 55 في اتفاقية الأمم المتحدة لقانون البحار لعام 1982؛ هي منطقة...

Radio broadcast station targeting a foreign country For the band, see The Border Blasters. X station redirects here. For the Novation synthesizer, see X-Station. This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these template messages) This article may be in need of reorganization to comply with Wikipedia's layout guidelines. Please help by editing the article to make improvements to the overall structure. (Novemb...

Lars RasmussenLars Rasmussen tahun 2007Photo credit: Charlie BrewerTempat tinggalSan Francisco, California, Amerika SerikatKebangsaanDenmarkAlmamaterAarhus UniversityUniversity of EdinburghUniversity of California, BerkeleyDikenal atasGoogle Maps, Google WavePenghargaanPearcey Award (2010)Karier ilmiahBidangIlmu komputerInstitusiGoogle, FacebookPembimbing doktoralAlistair Sinclair Lars Eilstrup Rasmussen adalah seorang ilmuwan komputer, pengembang perangkat lunak, dan pendiri pendamping Goog...

العلاقات الأوغندية الدومينيكانية أوغندا جمهورية الدومينيكان أوغندا جمهورية الدومينيكان تعديل مصدري - تعديل العلاقات الأوغندية الدومينيكانية هي العلاقات الثنائية التي تجمع بين أوغندا وجمهورية الدومينيكان.[1][2][3][4][5] مقارنة بين البل�...

