Algorytm Borůvki
|
Read other articles:
Brannenburg. Brannenburg adalah kota yang terletak di distrik Rosenheim di Bayern, Jerman. Kota Brannenburg memiliki luas sebesar 33.66 km². Brannenburg pada tahun 2006, memiliki penduduk sebanyak 5.663 jiwa. lbsKota dan kotamadya di Rosenheim Albaching Amerang Aschau im Chiemgau Babensham Bad Aibling Bad Endorf Bad Feilnbach Bernau am Chiemsee Brannenburg Breitbrunn am Chiemsee Bruckmühl Chiemsee Edling Eggstätt Eiselfing Feldkirchen-Westerham Flintsbach Frasdorf Griesstätt Großkar...

Entoprocta TaksonomiSuperkerajaanEukaryotaKerajaanAnimaliaSuperfilumSpiraliaFilumEntoprocta Familia Barentsiidae (Urnatellidae) Loxokalypodidae Loxosomatidae Pedicellinidae lbs Entoprocta, yang namanya berarti anus di dalam, adalah filum hewan air sebagian besar sesil, yang panjangnya 0,1-7 milimeter. Individu dewasa berbentuk goblet, pada batang yang relatif panjang. Mereka memiliki mahkota dari tentakel padat di mana silia menghasilkan arus air yang menarik partikel makanan ke mulut, dan ba...

Bey ArifinLahir(1917-09-29)29 September 1917 Parak Laweh, Tilatang Kamang, Agam, Hindia BelandaMeninggal30 April 1995(1995-04-30) (umur 77)Surabaya, Jawa TimurKebangsaanIndonesiaPekerjaanUlama, pengajar, penulisDikenal atasKetua Majelis Ulama Indonesia (MUI) Jawa Timur K.H. Bey Arifin (29 September 1917 – 30 April 1995) adalah seorang ulama, penulis dan pengajar Indonesia. Semasa hidupnya ia pernah dipercaya sebagai Ketua Majelis Ulama Indonesia (MUI) Jawa Timur. Riwayat...

Alfred KerrAlfred Kerr Lovis Corinth (1907) LahirAlfred Kempner(1867-12-25)25 Desember 1867Breslau, Silesia, Prusia(sekarang Wrocław, Polandia)Meninggal12 Oktober 1948(1948-10-12) (umur 80)Hamburg, JermanPekerjaanPenulis dan kritikus teaterSuami/istriIngeborg Thormählen (m. 1917; wafat 1918) Julia Weismann (m. 1920)AnakMichael Kerr Judith KerrKerabatMatthew Kneale (cucu) Alfred Kerr (né Kempner...

Pour les articles homonymes, voir Charles VIII. Charles VIII Portrait de Charles VIII, huile sur panneau de bois, école française du XVIe siècle, Chantilly, musée Condé. Titre Roi de France 30 août 1483 – 7 avril 1498(14 ans, 7 mois et 8 jours) Couronnement 30 mai 1484,en la Cathédrale de Reims Régent Anne de France (1483-1491) Prédécesseur Louis XI Successeur Louis XII Roi de Naples 22 février 1495 – 6 juillet 1495(4 mois et 14 jours) Prédécess...

يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوق بها. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (ديسمبر 2018) فيما يلي قائمة من قوائم العواصم. العواصم الوطنية قائمة المدن الكبرى حسب الدولة قائمة العواصم الوطنية حسب...

ملخص معلومات الملف الوصف مخطط معلومات بياني للدورة الثانية (2009) للجائزة العالمية للرواية العربية. المصدر تم تصميم الأيقونة بناء على تصاميم مشتقة من أنظر هنا، ومن أنظر هنا، ومن أنظر هنا. التاريخ 28 مارس، 2017، تم تعديل خطأ في النسخة الأولى وذلك في 27 أبريل، 2017. المنتج عمل شخصي. ال...

Halaman ini berisi artikel tentang aliran material vulkanik. Untuk lelehan batu (magma) pijar, lihat lava. Lahar dari erupsi Gunung Galunggung pada tahun 1982 Lahar (Inggris: volcanic mudflow) adalah aliran material vulkanik yang biasanya berupa campuran batu, pasir dan kerikil akibat adanya aliran air yang terjadi di lereng gunung (gunung berapi).[1] Di Indonesia khususnya, aktivitas aliran lahar ini akan meningkat seiring meningkatnya intensitas curah hujan. Aliran lahar sangat ...

Deep Blue SeaSutradaraRenny HarlinProduserAkiva Goldsman Robert Kosberg Tony Ludwig Alan RicheDitulis olehDuncan Kennedy, Donna Powers, Wayne PowersPemeranThomas JaneSaffron BurrowsLL Cool JMichael RapaportSamuel L. JacksonDistributorWarner BrothersTanggal rilis28 Juli 1999Durasi105 menitIMDbInformasi di IMDb Deep Blue Sea merupakan sebuah film horor yang dibuat pada tahun 1999. Film ini ditulis oleh Donna Powers, disutradarai oleh Renny Harlin. Pemain utama di film ini ialah Thomas Jane, Saf...

† Человек прямоходящий Научная классификация Домен:ЭукариотыЦарство:ЖивотныеПодцарство:ЭуметазоиБез ранга:Двусторонне-симметричныеБез ранга:ВторичноротыеТип:ХордовыеПодтип:ПозвоночныеИнфратип:ЧелюстноротыеНадкласс:ЧетвероногиеКлада:АмниотыКлада:Синапсиды�...

Neighborhood in Manhattan, New York City For the hamlet in upstate New York, see Rose Hill, New York. 40°44′31″N 73°58′59″W / 40.742°N 73.983°W / 40.742; -73.983 The 69th Regiment Armory on Lexington Avenue between 25th and 26th Streets Location in New York City Rose Hill is a neighborhood in the New York City borough of Manhattan,[1] between the neighborhoods of Murray Hill to the north and Gramercy Park to the south,[2] Kips Bay to the eas...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

此條目可能包含不适用或被曲解的引用资料,部分内容的准确性无法被证實。 (2023年1月5日)请协助校核其中的错误以改善这篇条目。详情请参见条目的讨论页。 各国相关 主題列表 索引 国内生产总值 石油储量 国防预算 武装部队(军事) 官方语言 人口統計 人口密度 生育率 出生率 死亡率 自杀率 谋杀率 失业率 储蓄率 识字率 出口额 进口额 煤产量 发电量 监禁率 死刑 国债 ...

Latin letter G with cedilla Latin letter G with cedilla Ģ, ģ (g-cedilla) is the 11th letter of the Latvian alphabet.[1] In Latvian, it has the IPA value /ɟ/, similar to the pronunciation of the ⟨g⟩ in argue. In ISO 9, Ģ is the official Latin transliteration of the Cyrillic letter Ӷ. External links Look up Ģ or ģ in Wiktionary, the free dictionary. Omniglot - writing systems & languages of the world References ^ Unicode Character Ģ (U+0122). Compart. Oak ...

Polish noblewoman Anna Zofia SapiehaPrincess Anna Zofia with her daughter and daughter-in-lawCoat of armsLis coat of armsBorn(1799-10-17)17 October 1799Saint-Germain-en-Laye, FranceDied24 November 1864(1864-11-24) (aged 65)Montpellier, FranceNoble familySapiehaconsortAdam Jerzy CzartoryskiIssueWitold CzartoryskiWładysław CzartoryskiIzabella Elżbieta CzartoryskaFatherAleksander Antoni SapiehaMotherAnna Zamoyska Princess Anna Zofia Sapieha (17 October 1799 – 24 November 1864) was a Po...

Austrian novelist and pacifist (1843–1914) Bertha von SuttnerSuttner c. 1906BornBertha Sophie Felicitas Gräfin Kinsky von Wchinitz und Tettau(1843-06-09)9 June 1843Prague, Kingdom of Bohemia,Austrian EmpireDied21 June 1914(1914-06-21) (aged 71)Vienna, Austria-HungaryOccupation(s)Pacifist, novelistSpouseArthur Gundaccar von SuttnerAwardsNobel Peace Prize, 1905Signature Bertha Sophie Felicitas Freifrau[1] von Suttner (pronounced [ˈbɛʁtaː fɔn ˈzʊtnɐ]; née&#...

The early Christians, like the early Jews, were vehemently opposed to astrology, even attributing it to demonic origin. The Church Fathers were willing to impose strong sanctions against astrology to protect their flocks. In A.D. 120, the noted mathematician Aquila Ponticus was excommunicated from the Church at Rome for astrological heresies.[1]A 17th-century fresco from the Eastern Orthodox Cathedral of Living Pillar in Georgia depicting Jesus within the Zodiac circle Ancient An ast...
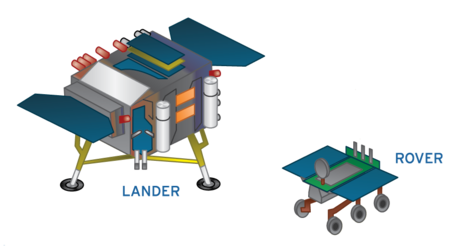
Chang'e 4Jenis misilander, rover BulanOperatorCNSACOSPAR ID2018-103ASATCAT no.43845Durasi misiLander: 12 bulanRover: 3 bulan[1] Properti wahanaMassa luncurLander: 1,200 kg[2]Rover: 140 kg[2]Massa mendaratTotal: ~1,200 kg; rover: 140 kgDimensiRover: 1.5 × 1.0 × 1.0 m[3] Awal misiTanggal luncurLander dan rover: 7 Desember 2018, 18:23 UTC[4]Roket peluncurLong March 3B[5][6]Tempat peluncuranPusat Peluncuran Satelit Xichang Robot penje...

Pada awal abad ke-20 didatangkan sapi penghasil susu Fries-Holland ke Jawa. Pertanian Umum Agribisnis Agroindustri Agronomi Ilmu pertanian Jelajah bebas Kebijakan pertanian Lahan usaha tani Mekanisasi pertanian Menteri Pertanian Perguruan tinggi pertanian Perguruan tinggi pertanian di Indonesia Permakultur Pertanian bebas ternak Pertanian berkelanjutan Pertanian ekstensif Pertanian intensif Pertanian organik Pertanian urban Peternakan Peternakan pabrik Wanatani Sejarah Sejarah pertanian Sejar...

List of events ← 2019 2018 2017 2020 in Tanzania → 2021 2022 2023 Decades: 2000s 2010s 2020s See also: Other events of 2020 Timeline of Tanzanian history Events of 2020 in Tanzania. Incumbents President: John Magufuli Vice-President: Samia Suluhu Prime Minister: Kassim Majaliwa Chief Justice: Ibrahim Hamis Juma Events January January 31 – U.S. President Donald Trump restricts certain types of visa for Tanzanian citizens.[1] February February 2 – At least 40 people are ...












































