Ten artykuł dotyczy algorytmu rozwiązującego problem komiwojażera. Zobacz też: algorytm k najbliższych sąsiadów.

Algorytm najbliższego sąsiada

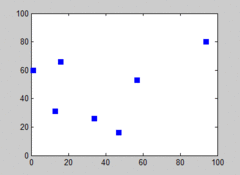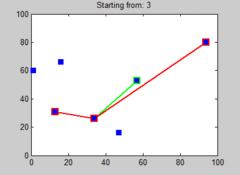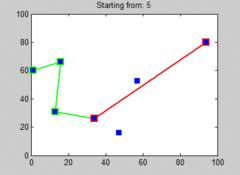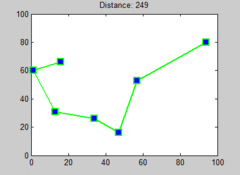
Przykładowe wykonanie algorytmu
Rodzaj	algorytm zachłanny
Złożoność
Czasowa	${\displaystyle O(n^{2})}$

Algorytm najbliższego sąsiada (ang. nearest neighbour algorithm, NN) – algorytm zachłanny służący do rozwiązywania problemu komiwojażera polegający na odwiedzaniu, począwszy od wybranego wierzchołka, wierzchołka znajdującego się najbliżej wierzchołka ostatnio odwiedzonego. Dla grafu pełnego o n wierzchołkach złożoność czasowa algorytmu wynosi ${\displaystyle O(n^{2})}$^[1].

Algorytm działa w następujący sposób^[2]:

1. Ustaw wybrany wierzchołek jako aktualny, oznacz go jako odwiedzony.
2. Znajdź ten spośród nieodwiedzonych wierzchołków, który jest połączony z aktualnym krawędzią o najmniejszej wadze.
3. Dołącz do rozwiązania krawędź łączącą aktualny wierzchołek z wierzchołkiem znalezionym w punkcie 2.
4. Oznacz wierzchołek znaleziony w punkcie 2 jako odwiedzony i ustaw go jako aktualny.
5. Jeśli pozostały jeszcze nieodwiedzone wierzchołki, przejdź do punktu 2.
6. Dołącz do rozwiązania krawędź łączącą aktualny wierzchołek z wierzchołkiem wybranym w punkcie 1, aby zamknąć cykl.

Algorytm nie daje gwarancji znalezienia rozwiązania optymalnego (problem komiwojażera jest problemem NP-trudnym, zatem nie jest znany dokładny algorytm działający w czasie co najwyżej wielomianowym). Rozwiązania wyznaczone przez algorytm są średnio o około 25% gorsze od optymalnych^[1].

Istnieją dane, dla których algorytm najbliższego sąsiada zwraca najgorsze możliwe rozwiązanie^[3]. Wynik działania algorytmu może różnić się w zależności od wyboru wierzchołka, od którego rozpoczyna się wyznaczanie cyklu.

Istnieje ulepszona wersja tego algorytmu o nazwie powtarzalny algorytm najbliższego sąsiada (ang. repetitive nearest neighbour algorithm, RNN), która polega na uruchomieniu algorytmu najbliższego sąsiada dla każdego możliwego wierzchołka startowego i wybraniu najmniejszego z rozwiązań. Złożoność takiego algorytmu to ${\displaystyle O(n^{3}).}$ I ten algorytm nie daje gwarancji znalezienia optymalnego rozwiązania, ale rozwiązania wyznaczone przez algorytm RNN są średnio o około 15% gorsze od optymalnych^[1].

• cykl Hamiltona