Octonion
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Read other articles:

Firik beralih ke halaman ini. Untuk hidangan sereal dari Mediterania timur, lihat Freekeh. Koordinat: 41°08′54″N 48°37′35″E / 41.14833°N 48.62639°E / 41.14833; 48.62639 FırıqFırıqKoordinat: 41°08′54″N 48°37′35″E / 41.14833°N 48.62639°E / 41.14833; 48.62639Negara AzerbaijanRayonQubaMunisipalitasAfurcaZona waktuUTC+4 (AZT) • Musim panas (DST)UTC+5 (AZT) Fırıq (juga Firik) adalah sebuah desa di Rayon Q...

Green space in Queens, New York Libra Triangle in November 2019. Libra Triangle is a 0.028 acres (0.011 ha) public green space located in the neighborhood of Elmhurst in Queens, New York, at the intersection of Broadway and Justice Avenue. Prior to its consolidation with New York City in 1898, Elmhurst was known as the town of Newtown. Its center of local government was at the site of this traffic triangle. In 1803, Newtown Town Hall was built on this site and expanded with into a courth...

Ang Muntinlupa primera klaseng dakbayan nahimutang sa Metro Manila, Pilipinas. Adunay kinatibok-an gidak-on nga 39.75 kilometros quadrado ug nahimutang nga nag-inusara nga distrito. Sumala sa census ni acting 2010, dunay 459,941 katawo. Ang gitudlo nga kodigo postal mao ang 1770 (CPO). Kinìng maong artikulo adunay kabahin sa Pilipinas mao usa ka Saha. Makatábang ka sa Wikipedya pinaági sa pag-uswág ug pag-punô niini.vte vteManila CaloocanLas PiñasMakati MalabonMandalu...

This article needs to be updated. The reason given is: Polling is needed for months later in the year. Please help update this article to reflect recent events or newly available information. (March 2024) This article is part of a series aboutJoe Biden Political positions Electoral history Early life and career Eponyms Family Honors Public image U.S. Senator from Delaware Judiciary Committee Bork hearings Thomas hearings 1994 Crime Bill Violence Against Women Act Foreign Relations Committee ...

Rok progresifEmerson, Lake dan Palmer tampil pada tahun 1992Nama lain Art rock rok klasik prog symphonic rock Sumber aliran Rok psikedelis musik progresif jazz folk klasik Sumber kebudayaanPertengahan ke akhir 1960an, Britania Raya dan Amerika SerikatBentuk turunan Krautrock[1] new-age music[2] occult rock[3] post-rock[4] symphonic pop[5] new wave Subgenre Canterbury scene[6] neo-progressive rock[7] Rock in Opposition[6] Genre ca...

American football player (born 1991) American football player Khalil MackMack with the Chicago Bears in 2019No. 52 – Los Angeles ChargersPosition:LinebackerPersonal informationBorn: (1991-02-22) February 22, 1991 (age 33)Fort Pierce, Florida, U.S.Height:6 ft 3 in (1.91 m)Weight:269 lb (122 kg)Career informationHigh school:Fort Pierce WestwoodCollege:Buffalo (2009–2013)NFL draft:2014 / Round: 1 / Pick: 5Career history Oakland Raiders (2014�...

Prison Architect Publikasi 6 Oktober 2015 Windows, MacOS, Linux6 Oktober 2015PlayStation 4, Xbox OneNA: 28 Juni 2016EU: 1 Juli 2016AU: 5 Juli 2016Xbox 3602 Agustus 2016iOS, Android25 Mei 2017Nintendo Switch20 Agustus 2018 GenreSimulasi konstruksi dan manajemenModel bisnisakses awal Bahasa Daftar Belanda, Inggris, Italia, Jepang, Jerman, Korea, Polandia, Portugis Brasil, Prancis, Rusia, Spanyol, Swedia, Tionghoa Sederhana, Tionghoa Tradisional dan Turki 60 Karakteristik teknisSistem operasiAn...
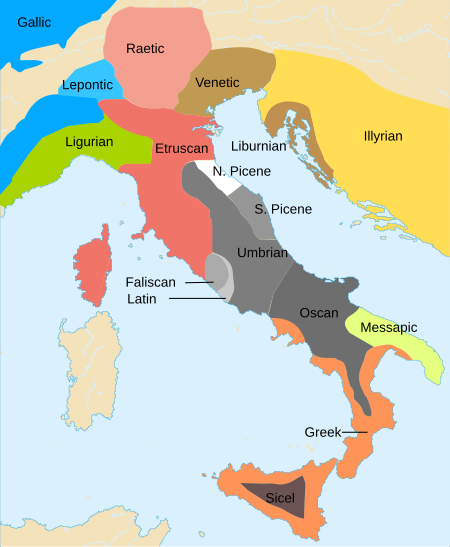
Roman conquest of Italy from 588 BC to 7 BC This article is about the unification of Italy by the Roman Republic. For Justinian's Italian campaign, see Gothic War (535–554). Roman expansion in Italy from 500 BC to 218 BC through the Latin War (light red), Samnite Wars (pink/orange), Pyrrhic War (beige), and First and Second Punic War (yellow and green). Cisalpine Gaul (238–146 BC) and Alpine valleys (16–7 BC) were later added. The Roman Republic in 500 BC is marked with dark red. Part o...

Methylrhenium trioxide Names IUPAC name Methyl(trioxo)rhenium(VII) Other names Methyltrioxorhenium(VII) Identifiers CAS Number 70197-13-6 Y 3D model (JSmol) Interactive image Abbreviations MTO ChemSpider 10621726 N ECHA InfoCard 100.202.821 PubChem CID 2734010 UNII 883D8RDD5Q CompTox Dashboard (EPA) DTXSID40370077 InChI InChI=1S/CH3.3O.Re/h1H3;;;; NKey: PQTLALPZRPFYIT-UHFFFAOYSA-N NInChI=1/CH3.3O.Re/h1H3;;;;/rCH3O3Re/c1-5(2,3)4/h1H3Key: PQTLALPZRPFYIT-YHFCCQKIAF...

土库曼斯坦总统土库曼斯坦国徽土库曼斯坦总统旗現任谢尔达尔·别尔德穆哈梅多夫自2022年3月19日官邸阿什哈巴德总统府(Oguzkhan Presidential Palace)機關所在地阿什哈巴德任命者直接选举任期7年,可连选连任首任萨帕尔穆拉特·尼亚佐夫设立1991年10月27日 土库曼斯坦土库曼斯坦政府与政治 国家政府 土库曼斯坦宪法 国旗 国徽 国歌 立法機關(英语:National Council of Turkmenistan) ...

此条目序言章节没有充分总结全文内容要点。 (2019年3月21日)请考虑扩充序言,清晰概述条目所有重點。请在条目的讨论页讨论此问题。 哈萨克斯坦總統哈薩克總統旗現任Қасым-Жомарт Кемелұлы Тоқаев卡瑟姆若马尔特·托卡耶夫自2019年3月20日在任任期7年首任努尔苏丹·纳扎尔巴耶夫设立1990年4月24日(哈薩克蘇維埃社會主義共和國總統) 哈萨克斯坦 哈萨克斯坦政府...

Filipino TV series or program Andar ng mga BalitaCreated byABC Development Corporation Nation Broadcasting CorporationDeveloped byNews5Directed byBenedict CarlosPresented byMartin AndanarChi BocoboCountry of originPhilippinesOriginal languageFilipinoNo. of episodesn/a (airs daily)ProductionExecutive producerEric MontasRunning time60 minutes Monday to Friday at 11:00 (PST)Original releaseNetworkAksyonTVReleaseFebruary 21, 2011 (2011-02-21) –July 11, 2014 (2014-07-11)RelatedBa...

2015 Philippine television show To the TopTitle cardGenreReality competitionPresented byChristian BautistaJudges Ryan Cayabyab Moy Ortiz Sweet Plantado OJ Mariano Country of originPhilippinesOriginal languages Tagalog English No. of episodes20ProductionProduction locationsQuezon City, PhilippinesCamera setupMultiple-camera setupRunning time30–45 minutesProduction companies GMA Entertainment TV GMA Public Affairs Original releaseNetworkGMA NetworkReleaseJuly 25 (2015-07-25) –Sept...

本條目存在以下問題,請協助改善本條目或在討論頁針對議題發表看法。 此條目需要編修,以確保文法、用詞、语气、格式、標點等使用恰当。 (2013年8月6日)請按照校對指引,幫助编辑這個條目。(幫助、討論) 此條目剧情、虛構用語或人物介紹过长过细,需清理无关故事主轴的细节、用語和角色介紹。 (2020年10月6日)劇情、用語和人物介紹都只是用於了解故事主軸,輔助�...

一中同表,是台灣处理海峡两岸关系问题的一种主張,認為中华人民共和国與中華民國皆是“整個中國”的一部份,二者因為兩岸現狀,在各自领域有完整的管辖权,互不隶属,同时主張,二者合作便可以搁置对“整个中國”的主权的争议,共同承認雙方皆是中國的一部份,在此基礎上走向終極統一。最早是在2004年由台灣大學政治学教授張亞中所提出,希望兩岸由一中各表�...

Liar GameBerkas:Liar Game vol01.jpgTankōbon pertama Liar Game yang dipublikasikan oleh Shueisha menampilkan Nao Kanzaki (tengah) dan Shinichi Akiyama (kanan) di sampul.ライアーゲーム(Raiā Gēmu)GenreDrama, Thriller psikologi, Gambling, Misteri MangaPengarangShinobu KaitaniPenerbitShueishaMajalahMingguan Young JumpDemografiSeinenTerbit2005 – sekarangVolume16 (Daftar volume) Drama televisiLiar GameSutradaraHiroaki Matsuyama, Ayako TaibokuMusikYasutaka NakataSaluranasliFuji TVTayang 1...

French painter (1783–1855) This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: Jean-Baptiste Paulin Guérin – news · newspapers · books · scholar · JSTOR (December 2014) (Learn how and when to remove this message) Self-portrait (c.1817) Jean-Baptiste Paulin Guérin (25 March 1783, in Toulon – 19 January 1855...
توقاد الإحداثيات 40°21′10″N 36°33′52″E / 40.352777777778°N 36.564444444444°E / 40.352777777778; 36.564444444444 [1] تقسيم إداري البلد تركيا[2][3] التقسيم الأعلى تركيا العاصمة توقاد التقسيمات الإدارية الموصأرتوفاباسيفتليكأربانيكساربازار (مدينة)رشدية (مدينة)س�...

Cohomology with real coefficients computed using differential forms For Grothendieck's de Rham cohomology of varieties, see algebraic de Rham cohomology. Vector field corresponding to a differential form on the punctured plane that is closed but not exact, showing that the de Rham cohomology of this space is non-trivial. In mathematics, de Rham cohomology (named after Georges de Rham) is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topo...

هذه المقالة تحتاج للمزيد من الوصلات للمقالات الأخرى للمساعدة في ترابط مقالات الموسوعة. فضلًا ساعد في تحسين هذه المقالة بإضافة وصلات إلى المقالات المتعلقة بها الموجودة في النص الحالي. (أغسطس 2019) كوبا ليبرتادوريس 1969 تفاصيل الموسم كوبا ليبرتادوريس النسخة 10 التاريخ بدا...






























