코시 곱
|
Read other articles:

HipernefromaGambar histopatologi terhadap kanker sel ginjal. Spesimen nefrektomi. Hematoxylin-eosin.Informasi umumSpesialisasiOnkologi Hipernefroma (bahasa Inggris: Renal cell carcinoma, RCC, hypernephroma) adalah bentuk kanker berasal dari lapisan tubulus renal proksimal, tubulus yang berbelit belit dan berlokasi dekat glomerulus di dalam ginjal. Jenis kanker ini adalah jenis kanker ginjal yang paling terumum dalam orang dewasa, bertanggung jawab untuk sekitar 90% - 95% kasus yang ...

Bank perdagangan kekaisaran KanadaCanadian Imperial Bank of CommerceBanque Canadienne Impériale de CommerceJenisUmumKode emitenTSX: CM NYSE: CMIndustriJasa keuangan, perbankanDidirikan1867KantorpusatToronto, Ontario, KanadaTokohkunciGerald T. McCaughey, CEOPendapatan$12,1 miliar CAD (2010)Laba bersih $2,5 miliar CAD (2010)Total aset$352,0 miliar CAD (2010)Karyawan42.354 (penuh waktu, 2010)AnakusahaCIBC World MarketsCIBC Retail MarketsCIBC Imperial ServiceCIBC Wood GundySitus webwww.cibc...

Vous lisez un « bon article » labellisé en 2021. La foudre est l'un des phénomènes électriques les plus impressionnants qui existent. L’électricité est l'ensemble des phénomènes physiques associés à la présence et au mouvement de la matière qui possède une propriété de charge électrique. L'électricité est liée au magnétisme, les deux faisant partie du phénomène de l'électromagnétisme, tel que décrit par les équations de Maxwell. Divers phénomènes cou...

Earl Warren Ketua Mahkamah Agung Amerika Serikat ke-14Masa jabatan5 Oktober 1953 – 23 Juni 1969Dicalonkan olehDwight D. Eisenhower PendahuluFred M. VinsonPenggantiWarren E. BurgerGubernur California ke-30Masa jabatan4 Januari 1943 – 5 Oktober 1953WakilFrederick F. HouserGoodwin Knight PendahuluCulbert OlsonPenggantiGoodwin KnightKejaksaan Agung California ke-20Masa jabatan3 Januari 1939 – 4 Januari 1943GubernurCulbert Olson PendahuluUlysses S. WebbPenggantiRob...
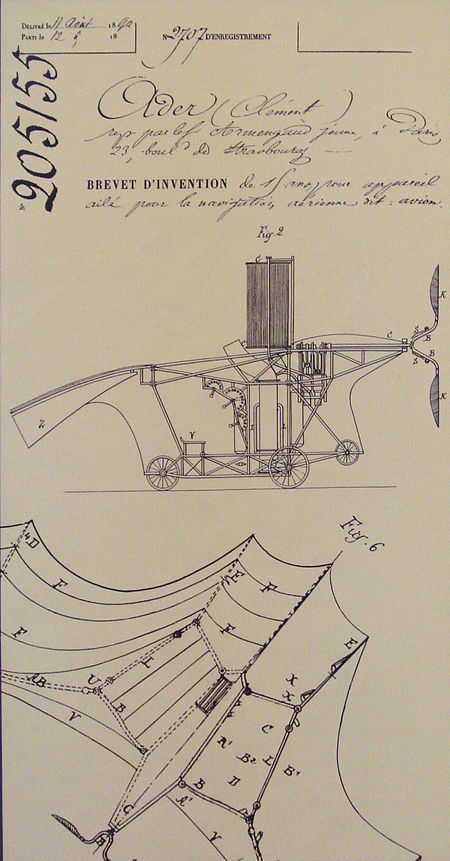
Chronologies Affiche présentant une exhibition ethnographique de Somalis au Jardin d'acclimatation à Paris en août et septembre 1890.Données clés 1887 1888 1889 1890 1891 1892 1893Décennies :1860 1870 1880 1890 1900 1910 1920Siècles :XVIIe XVIIIe XIXe XXe XXIeMillénaires :-Ier Ier IIe IIIe Chronologies géographiques Afrique Afrique du Sud, Algérie, Angola, Bénin, Botswana, Burkina Faso, Burundi, Cameroun, Cap-Vert, Ré...

Natural-gas-fired power station in California Gateway Generating StationCountryUnited StatesLocation3225 Wilbur Avenue, Antioch, California[1]Coordinates38°01′03″N 121°45′31″W / 38.0175°N 121.7587°W / 38.0175; -121.7587 (Gateway Generating Station)StatusOperationalConstruction began2001Commission dateJanuary 4, 2009Owner(s)Pacific Gas & ElectricOperator(s)Pacific Gas & ElectricThermal power station Primary fu...

List of bodily actions used as nonverbal communication This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (June 2022) (Learn how and when to remove this message) People often use gestures during heated or tense arguments, such as at this political demonstration (2007). Gestures are a form of nonverbal communication in which visible bodily actions are used to comm...

American politician William Thomas FitzgeraldMember of the U.S. House of Representativesfrom Ohio's 4th districtIn officeMarch 4, 1925 – March 3, 1929Preceded byJohn L. CableSucceeded byJohn L. Cable Personal detailsBorn(1858-10-13)October 13, 1858Greenville, OhioDiedJanuary 12, 1939(1939-01-12) (aged 80)Greenville, OhioResting placeGreenville CemeteryPolitical partyRepublicanAlma mater National Normal University College of Wooster William Thomas Fitzgerald (Octobe...

TUT7 المعرفات الأسماء المستعارة TUT7, PAPD6, zinc finger CCHC-type containing 6, TENT3B, ZCCHC6, terminal uridylyl transferase 7 معرفات خارجية الوراثة المندلية البشرية عبر الإنترنت 613467 MGI: MGI:2387179 HomoloGene: 51941 GeneCards: 79670 علم الوجود الجيني الوظيفة الجزيئية • نشاط انتقالي• nucleotidyltransferase activity• ربط أيون الزنك• ربط أيون فلزي�...

هنودمعلومات عامةنسبة التسمية الهند التعداد الكليالتعداد قرابة 1.21 مليار[1][2]تعداد الهند عام 2011ق. 1.32 مليار[3]تقديرات عام 2017ق. 30.8 مليون[4]مناطق الوجود المميزةبلد الأصل الهند البلد الهند الهند نيبال 4,000,000[5] الولايات المتحدة 3,982,398[6] الإمار...

French woman interred at the Panthéon Sophie BerthelotBornSophie Caroline Niaudet(1837-02-17)February 17, 1837Nantes, FranceDiedMarch 18, 1907(1907-03-18) (aged 70)Paris, FranceResting placePanthéonKnown forFirst woman interred at the PanthéonSpouseMarcellin Berthelot (m. 1861–1907)ChildrenAndré BerthelotPhilippe BerthelotRelativesLouis-François-Clement Breguet (uncle) Sophie Caroline Berthelot (née Niaudet; February 17, 1837 – March 18, 1907)[1] became the first w...
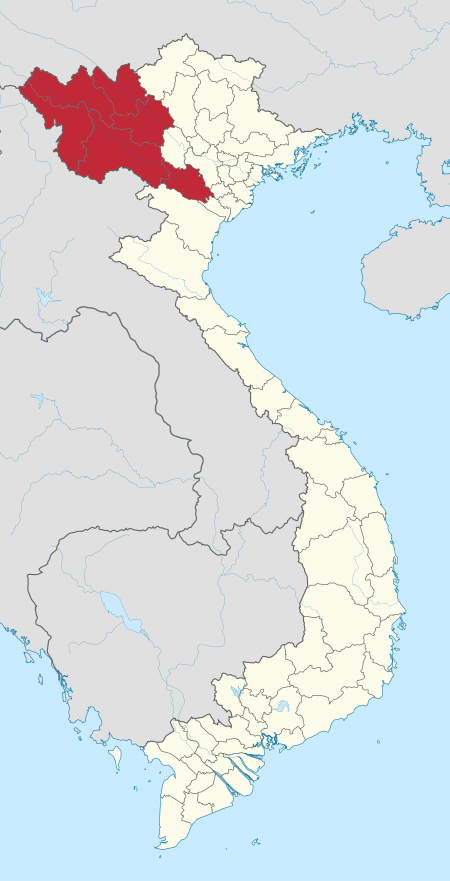
You can help expand this article with text translated from the corresponding article in Vietnamese. (March 2009) Click [show] for important translation instructions. View a machine-translated version of the Vietnamese article. Machine translation, like DeepL or Google Translate, is a useful starting point for translations, but translators must revise errors as necessary and confirm that the translation is accurate, rather than simply copy-pasting machine-translated text into the English ...

Direct reporting unit and U.S. Army's branch for military engineering This article needs additional citations for verification. Please help improve this article by adding citations to reliable sources. Unsourced material may be challenged and removed.Find sources: United States Army Corps of Engineers – news · newspapers · books · scholar · JSTOR (February 2022) (Learn how and when to remove this message) United States Army Corps of EngineersUSACE Shou...

Industrial process based on lost-wax casting For investment casting in art, see Lost-wax casting. Inlet-outlet cover of a valve for a nuclear power station produced using investment casting Investment casting is an industrial process based on lost-wax casting, one of the oldest known metal-forming techniques.[1] The term lost-wax casting can also refer to modern investment casting processes. Investment casting has been used in various forms for the last 5,000 years. In its earliest fo...

Portello tombale della cultura di Castelluccio. La cultura di Castelluccio è la principale espressione dell'Antica Età del bronzo siciliana, situata nel range cronologico 2300 a.C. - 1700 a.C. circa. L'eponimo è la omonima località posta tra Noto e Siracusa indagata nel XIX secolo dall'archeologo Paolo Orsi[1]. La definizione venne coniata dall'archeologo Luigi Bernabò Brea il quale riscontrò una omogeneità culturale di certe aree della Sicilia nell'antica Età del Bronzo. In q...

Serie A1 GAFAltri nomiSerie A1 di Ginnastica Artistica Femminile Sport Ginnastica artistica Tiposquadre di club Categoriafemminile Federazione FGI Paese Italia TitoloCampione d'Italia Cadenzaannuale DisciplineVolteggioCorpo liberoParallele asimmetricheTrave Partecipanti12 Formula3 prove più final six Retrocessione inSerie A2 GAF StoriaFondazione1987 Numero edizioni35 al 2021 Detentrice Brixia Record vittorie Brixia (19) Scudetto Modifica dati su Wikidata · Manuale Martin...

معهد هندسة البرمجياتنوع البحثMultiprogramوظيفة700Address4500 Fifth Avenueالموقعبيتسبرغ (بنسيلفانيا)، بنسيلفانيا، الولايات المتحدة40°26′48″N 79°57′00″W / 40.4466°N 79.9500°W / 40.4466; -79.9500رموز بريد الولايات المتحدة15213AffiliationsDepartment of Defense، Department of the Armyالهيئة الإداريةجامعة كارنيغي ميلونWebsit...

3°8′N 101°41′E / 3.133°N 101.683°E / 3.133; 101.683 提示:此条目页的主题不是大吉隆坡。 吉隆坡KL首都、联邦直辖区吉隆坡联邦直辖区Wilayah Persekutuan Kuala LumpurFederal Territory of Kuala Lumpur其他文字轉寫 • 马来语Kuala Lumpurکوالا لومڤور(爪夷文) • 英语Kuala Lumpur • 粵语吉隆坡gat1 lung4 bo1(粤拼) • 淡米尔语கோல�...

Recorded laughter in broadcast comedy show For the 2023 album by The National, see Laugh Track. This article possibly contains original research. Relevant discussion may be found on the talk page. Please improve it by verifying the claims made and adding inline citations. Statements consisting only of original research should be removed. (May 2020) (Learn how and when to remove this message) An example laugh track recorded in 2009 A laugh track (or laughter track) is an audio recording consis...

Genus of flightless birds This article is about the genus of birds. For other uses, see Cassowary (disambiguation). CassowaryTemporal range: 5–0 Ma PreꞒ Ꞓ O S D C P T J K Pg N ↓ Early Pliocene – Recent Montage of three species; left to right: southern cassowary, northern cassowary and dwarf cassowary Scientific classification Domain: Eukaryota Kingdom: Animalia Phylum: Chordata Class: Aves Infraclass: Palaeognathae Order: Casuariiformes Family: CasuariidaeKaup, 1847[1&#...
































