인자 (대수기하학)
|
Read other articles:

The history of Tufts University, originally Tufts College, can be traced back to 1847 when the Universalist Church set up convention for the creation of a university for the parish. In 1858, the college was established when Boston businessman Charles Tufts donated 20 acres of land to the church to establish the college. It is the third oldest college that was founded in the Boston area.[1] During the 19th century the college grew. The official college seal, bearing the motto Pax et Lu...

Chris Kirkland Informasi pribadiNama lengkap Christopher Edmund KirklandTanggal lahir 2 Mei 1981 (umur 42)Tempat lahir Barwell, Leicestershire, InggrisTinggi 1,91 m (6 ft 3 in)[1]Posisi bermain Penjaga gawangInformasi klubKlub saat ini Sheffield WednesdayNomor –Karier senior*Tahun Tim Tampil (Gol)1998–2001 Coventry City 24 (0)2001–2006 Liverpool 25 (0)2005–2006 → West Bromwich Albion (pinjaman) 10 (0)2006 → Wigan Athletic (pinjaman) 1 (0)2006–2012 Wi...

Not to be confused with Troutdale, Virginia. Town in Virginia, United StatesTroutville, VirginiaTownMill Creek Baptist Church LogoLocation of Troutville, VirginiaCoordinates: 37°24′55″N 79°52′37″W / 37.41528°N 79.87694°W / 37.41528; -79.87694CountryUnited StatesStateVirginiaCountyBotetourtArea[1] • Total0.69 sq mi (1.79 km2) • Land0.69 sq mi (1.79 km2) • Water0.00 sq mi (0.0...

Radio station in Tacoma, Washington Some of this article's listed sources may not be reliable. Please help improve this article by looking for better, more reliable sources. Unreliable citations may be challenged and removed. (July 2018) (Learn how and when to remove this template message) KHTPTacoma, WashingtonBroadcast areaSeattle metropolitan areaFrequency103.7 MHz (HD Radio)BrandingHot 103-7ProgrammingFormatClassic hip-hopAffiliationsCompass Media NetworksOwnershipOwnerAudacy, Inc.(Audacy...

Untuk kegunaan lain, lihat Get Married (disambiguasi). Get Married the SeriesGenre Drama Roman Komedi PembuatStarvisionDitulis oleh Daniel Tito Marlis Sibrani SutradaraM HaikalPemeran Acha Septriasa Adipati Dolken Meriam Bellina Jaja Mihardja Arya Saloka Miqdad Addausy Rendy Samuel Alessia Cestaro Fandy Christian Prilly Latuconsina Penggubah lagu temaSlank & Nirina ZubirLagu pembukaCubit Cubitan oleh Slank feat. Nirina ZubirLagu penutupCubit Cubitan oleh Slank feat. Nirina ZubirNegara asa...

Public park in Queens, New York Doughboy ParkDoughboy statue at entrance to parkTypeUrban parkLocationWoodside, Queens, New York CityCoordinates40°44′46.58″N 73°54′31.52″W / 40.7462722°N 73.9087556°W / 40.7462722; -73.9087556 (Doughboy Park)Area1.71 acres (0.69 ha)Created1957Operated byNew York CityOpenAll year Doughboy Park is a 1.71-acre (6,900 m2) New York City public park in the Woodside neighborhood of Queens. It is located on a ...

此條目可参照英語維基百科相應條目来扩充。 (2021年5月6日)若您熟悉来源语言和主题,请协助参考外语维基百科扩充条目。请勿直接提交机械翻译,也不要翻译不可靠、低品质内容。依版权协议,译文需在编辑摘要注明来源,或于讨论页顶部标记{{Translated page}}标签。 约翰斯顿环礁Kalama Atoll 美國本土外小島嶼 Johnston Atoll 旗幟颂歌:《星條旗》The Star-Spangled Banner約翰斯頓環礁�...

SMA Negeri 1 KlatenSmansa Klaten, Padmawijaya, Kampus 13InformasiDidirikan5 November 1957JenisNegeriAkreditasiA[1]Nomor Statistik Sekolah301046002001Nomor Pokok Sekolah Nasional20309676MotoPadmawijayaMaskotChiku si burung hantuKetua KomiteDrs. Sumargana, M.SJumlah kelas30 Kelas Reguler,3 Kelas Unggulan OSN (total 33 kelas)Jurusan atau peminatanIlmu Pengetahuan Alam dan Ilmu Pengetahuan SosialRentang kelasX, XI IPA-IPS, XI IPA (OSN), XII IPA-IPS, XII IPA (OSN)KurikulumKurikul...

本表是動態列表,或許永遠不會完結。歡迎您參考可靠來源來查漏補缺。 潛伏於中華民國國軍中的中共間諜列表收錄根據公開資料來源,曾潛伏於中華民國國軍、被中國共產黨聲稱或承認,或者遭中華民國政府調查審判,為中華人民共和國和中國人民解放軍進行間諜行為的人物。以下列表以現今可查知時間為準,正確的間諜活動或洩漏機密時間可能早於或晚於以下所歸�...

Pemberontakan dalam negeri terhadap apartheidNelson Mandela membakar buku izin masuk miliknya pada tahun 1960 sebagai bagian dari kampanye pembangkangan sipilTanggal17 Desember 1950 – 27 April 1994(43 tahun, 4 bulan, 1 minggu dan 3 hari)[note 1]LokasiAfrika SelatanHasil Kebuntuan militer antara MK and satuan pengamanan Afrika Selatan [3][4] Negosiasi bilateral untuk mengakhiri apartheid[1] Penghapusan apartheid pada tahun 1991 Pembubaran b...

County in Vermont, United States County in VermontOrleans CountyCountyOrleans County Courthouse in Newport (city)Location within the U.S. state of VermontVermont's location within the U.S.Coordinates: 44°50′40″N 72°13′06″W / 44.844402°N 72.218239°W / 44.844402; -72.218239Country United StatesState VermontFounded1799Named forOrléans, FranceShire TownNewportLargest cityDerbyArea • Total721 sq mi (1,870 km2) • ...

Zoologi Cabang Antropologi · Antrozoologi · ApiologiAraknologi · Artropodologi · CetologiConchologi · Entomologi · EtologiHelminthologi · Herpetologi · IktiologiMalacologi · Mammalogi · MyrmecologiNematologi · Neuroetologi · OrnitologiPaleozoologi · Planktologi · PrimatologiZoosemiotik Zoologis terkemuka Karl Ernst von Baer · Geor...
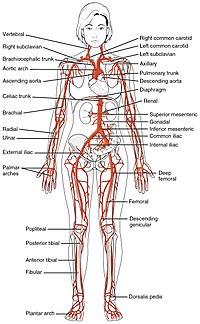
Cấu tạo của tĩnh mạch Tiết diện dọc tĩnh mạch minh họa van giữ cho huyết lưu không bị bơm ngược hướng Tĩnh mạch hay Vein là mạch máu thuộc hệ tuần hoàn trong cơ thể, dẫn máu trở về tim (đối ngược với động mạch đưa máu từ tim ra). Thường thì máu trong tĩnh mạch có lượng oxy thấp khi đưa máu từ các mô trong cơ thể về tim. Hai ngoại lệ là tĩnh mạch rốn và tĩnh mạch phổi. Trong h...

Cet article est une ébauche concernant les Jeux olympiques et les Pays-Bas. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Pays-Bas aux Jeux olympiques d'été de 2000 Code CIO NED Lieu Sydney Participation 22e Athlètes 243 Porte-drapeau Anky van Grunsven (ouverture)Inge de Bruijn (clôture) MédaillesRang : 8e Or12 Arg.9 Bron.4 Total25 Historique Jeux olympiques d'été 1900 1908 1912 1920 1924 1928 193...

Jesaja Jesaja door Rafael Auteur (Traditioneel) Jesaja Tijd 750 v.Chr. - 2e eeuw v.Chr. Taal Hebreeuws Categorie Grote profeten Hoofdstukken 66 Vorige boek Hooglied (in de Tenach I en II Koningen) Volgende boek Jeremia Boekrol van Jesaja in het Hebreeuws Jesaja (Hebreeuws: יְשַׁעְיָהוּ, Jeshajahoe, redding van God) is een van de boeken van de Hebreeuwse Bijbel en wordt gerekend tot de grote profeten. In de Tenach wordt het boek gerekend tot de latere profeten (Neviiem Acharoniem)...

Cet article est une ébauche concernant la mer et la Norvège. Vous pouvez partager vos connaissances en l’améliorant (comment ?) selon les recommandations des projets correspondants. Dronning Maud Type paquebot Histoire Commanditaire Det Nordenfjeldske Dampskipsselskap Constructeur Fredrikstad Mekaniske Verksted Fredrikstad Norvège Lancement 8 mai 1925 Armé 3 juillet 1925 Statut Coulé le 1er mai 1940 Caractéristiques techniques Longueur 71,63 m Maître-bau 11,49 m Tira...

This article relies largely or entirely on a single source. Relevant discussion may be found on the talk page. Please help improve this article by introducing citations to additional sources.Find sources: Antoine-François-Claude Ferrand – news · newspapers · books · scholar · JSTOR (February 2012) Antoine François Claude, comte Ferrand (4 July 1751 – 17 January 1825), French statesman and political writer, was born in Paris, and became...
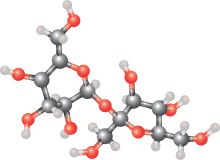
Disambiguazione – Se stai cercando il personaggio dei fumetti, vedi Molecola (personaggio). Disambiguazione – Se stai cercando la bibita alla cola, vedi MoleCola (bibita). Modello della molecola del saccarosio (principale componente dello zucchero da tavola) In fisica e chimica, la molecola (dal latino scientifico molecula, derivato a sua volta da moles, che significa mole, cioè piccola quantità) è un'entità elettricamente neutra composta da due o più atomi uniti da un legame covale...

Franz KlammerFranz Klammer con una della cinque Coppe del Mondo di discesa libera vinte in carrieraNazionalità Austria Altezza183 cm Peso79 kg Sci alpino SpecialitàDiscesa libera, slalom gigante, combinata SquadraWSV Unterdrautal[1] Termine carriera1985 Palmarès Competizione Ori Argenti Bronzi Olimpiadi 1 0 0 Mondiali 2 1 0 Trofeo Vittorie Coppa del Mondo - Discesa 5 trofei Vedi maggiori dettagli Modifica dati su Wikidata · Manuale Franz Klammer (Mooswald, 3 dicemb...

لمعانٍ أخرى، طالع بني حسان (توضيح). بني حسان الإحداثيات 35°34′02″N 10°48′31″E / 35.567222222222°N 10.808611111111°E / 35.567222222222; 10.808611111111 تقسيم إداري البلد تونس[1] التقسيم الأعلى ولاية المنستير معلومات أخرى 5014 رمز جيونيمز 2472732 الموقع الرسمي الموقع ا�...




























































![{\displaystyle \operatorname {Spec} \mathbb {C} [x,y,z]/(xy-z^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29b539d4d422c0b9881de3fe6750ae01524fce98)
![{\displaystyle \operatorname {Spec} \mathbb {C} [x,y,z]/((y)\cap (z))\subset \operatorname {Spec} \mathbb {C} [x,y,z]/(xy-z^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70b9473f582c6f41af7e4c1f0b88c9a21fa475f2)









































